355 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

За 21 день больному потребуется ​$$0,5\cdot2\cdot21=21$$​ гр лекарства

В одной упаковке ​$$10\cdot0,5=5$$​ гр лекарства по условию

Значит наименьшее кол-во упаковок равно $$5$$ ($$25​$$ гр лекарства)

$$-7-4=-11$$

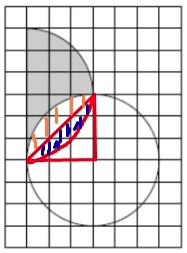
$$S=\frac{9π}{2}−2x​$$

$$2x$$​ – это сумма площадей оранжевого и синего сектора, исходя из симметрии они равны.

Найдем площадь оранжевого кругового сегмента, это будет площадь сектора – площадь прямоугольного треугольника.

$$x=\frac{πR^2\cdot ϕ}{2π}−0,5R^2\cdot\sin ϕ=\frac{9π}{4}−\frac{9}{2}$$​ (фи это $$90^{\circ}$$ или $$\frac{\pi}{2}$$)

​$$S=9$$

Пусть всего было $$100$$ щитов

Тогда щитов первого сорта ​$$100−5−31=64​$$

$$P(A)=\frac{64}{95}≈0,67$$

$$x^{\lg4}=4^{\lg x}​$$ (доказывается это очень легко, достаточно прологарифмировать)

Теперь это уравнение легко решается

$$2^{2\lg x+1}=2^5​$$

$$​2\lg x+1=5$$​

$$\lg x=2$$​

$$​x=100$$

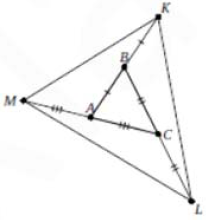
Достроим $$MB$$. $$\frac{S_{ABC}}{S_{MBA}}=\frac{AC}{MA}=1\Rightarrow S_{MBA}=1$$.

Аналогично, $$S_{MBK}=S_{MBA}=1; S_{KBC}=S_{KCL}=1; S_{ACL}=S_{LAM}=1$$. Тогда $$S_{MKL}=7$$.

$$V(t)=x'(t)=3t^2−2t−12​$$

$$​3t^2−2t−12=9​$$

$$​t=3$$​ (время неотрицательно!)

$$V_{полусфера}=\frac{2}{3}πR^3​$$

​$$V_{стакан}=π\frac{R^2}{9}\cdot2R=\frac{2}{9}πR^3$$

$$​36^{x−6}\cdot36^{6,5−x}=36^{0,5}=6$$

Чем выше скорость, тем выше давление воды. Нам нужно найти минимальную скорость при которой вода не будет выливаться, т.е. скорость при которой $$P=0$$, т.е. вода можно сказать “зависнет”.

$$0=\frac{v^2}{L}-g$$

$$​V=2,5$$

Пусть $$V$$​ – скорость Вани, а ​$$w$$​ – скорость эскалатора.

Тогда скорость мальчика относительно земли равна

1) Когда Ваня бежит вниз​ $$(V+w)\cdot t_1=S​$$, ​$$S$$​ – это путь, который прошел мальчик (через ступеньки)

2) Когда Ваня поднимается вверх ​$$(V−w)\cdot t_2=S$$​

Скорость мальчика относительно эскалатора

$$\left\{\begin{matrix} V\cdot t_1=40\\ V\cdot t_2=60 \end{matrix}\right.$$

Решаем эту простую систему уравнений, выразим времена и поставим в первые два уравнения

$$t_1=40V​, t_2=\frac{V}{60}$$​

$$(V+w)\cdot40V=S​$$

$$​(V−w)\cdot\frac{60}{V}=S​$$

Тогда

​$$V+w=S\cdot\frac{V}{40}$$​

​$$V−w=S\cdot\frac{V}{60}$$​

Сложим эти два уравнения

$$​2V=\frac{S\cdot V}{40}+\frac{S\cdot V}{60}​$$

Поделим это выражение на $$V$$, и выразим $$S$$

$$​2=\frac{S}{40}+\frac{S}{60​}$$

$$2=\frac{60S+40S}{40\cdot60}$$​, а $$​100S=2\cdot40\cdot60​$$

$$​S=48$$

Найдём критические точки:

​$$y'=2−\frac{2}{x+3}=0​$$

$$\frac{​x+3−1}{x+3}=0​$$

​$$x=−2$$​ – точка минимума

$$​x=−3​$$

​$$y(−2)=−1$$