320 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.

Установка двух счётчиков воды (холодной и горячей) стоит 3300 рублей. До установки счётчиков за воду платили 800 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 300 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?

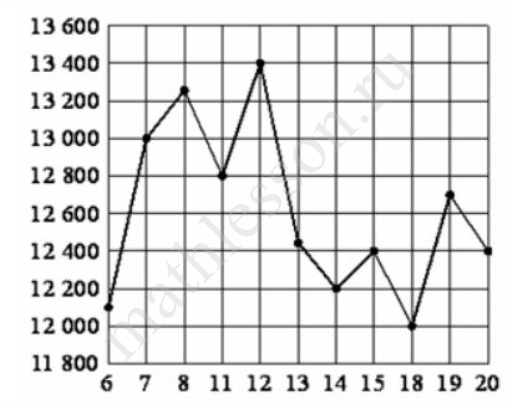
На рисунке жирными точками показана цена тонны никеля на момент закрытия биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали - цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена тонны никеля на момент закрытия торгов была наименьшей за указанный период.

На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 56. Найдите площадь закрашенной фигуры.

Найдите вероятность того, что произведение трех последних цифр случайно выбранного телефонного номера чётно.

Решите уравнение $${27}^{2x-1}={\left(\frac{1}{9}\right)}^{2x+4}$$

В равнобедренном треугольнике АВС с основанием АВ угол С равен $$48{}^\circ $$. Найдите угол между стороной АВ и высотой АН этого треугольника.

На рисунке изображен график $$y=f'\left(x\right)$$ - производной непрерывной функции $$f(x)$$, определенной на интервале $$\left(-4;7\right)$$. Найдите количество точек минимума функции $$f(x)$$, принадлежащих отрезку $$\left[-3;6\right]$$.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 6. Диагональ параллелепипеда равна 9. Найдите площадь поверхности параллелепипеда.

Найдите значение выражения $$\frac{{{\log }_9 10\ }}{{{\log }_9 11\ }}+{{\log }_{11} 0,1\ }$$

Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону $$\varphi =\omega t+\frac{\beta t^2}{2}$$, где t - время в минутах, $$\omega =40{}^\circ $$/мин - начальная угловая скорость вращения катушки, а $$\beta =4{}^\circ $$/мин$${}^{2 }$$- угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки $$\varphi $$ достигнет $$3000{}^\circ $$.

Определите время после начала работы лебёдки, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.

Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Найдите точку максимума функции $$f\left(x\right)=x^8\cdot e^{5x+6}$$.

а) Решите уравнение $$\sqrt{{\sin x\ }-{\cos x\ }}\left({ctg x\ }-\sqrt{3}\right)=0$$

б) Укажите корни этого уравнения, принадлежащие отрезку $$\left[\frac{3\pi }{2};3\pi \right]$$

В правильной треугольной пирамиде SABC с основанием АВС биссектрисы треугольника АВС пересекаются в точке О. Точка Р - середина ВС, на ребре AS отмечена точка N, причем PN перпендикулярна AS.

а) Доказать, что $${\sin \angle ASO\ }=\frac{NO}{PS}$$

б) Найдите расстояние от точки О до плоскости SBC, если $$AB=12\sqrt{3},\ {\sin \angle ASO\ }=\frac{3}{\sqrt{13}}$$

Решите неравенство $$\frac{{{\log }_3 (9x)\ }-13}{{({{\log }_3 x\ })}^2+{{\log }_3 x^4\ }}\le 1$$

В треугольнике АВС на стороне ВС выбрана точка М, причем $$\angle BAM=30{}^\circ $$. Прямая АМ пересекает окружность, описанную около треугольника АВС в точке N, отличной от А. Известно, что $$\angle BNC=105{}^\circ ,\ AB=2,AC=2\sqrt{6}$$.

а) Доказать, что $$BN:NC=1:\sqrt{2}$$

б) Найдите длину отрезка AN.

В феврале планируется взять кредит в банке в размере 3,6 млн рублей сроком на 24 месяца. Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на $$r\%$$ по сравнению с концом предыдущего месяца;

- со 2-го по 14 число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждый месяц долг должен уменьшиться на одну и ту же величину.

Известно, что с 5 по 10 месяц включительно, нужно выплатить банку 1,089 млн рублей.

Найдите процент банка $$r$$. Сколько будет выплачено банку за первые 12 месяцев?

Найдите все значения параметра $$a$$, при которых уравнение $$2^{\sqrt{x-0,5}}\cdot \left(\sqrt{a-8x^4}-2x^2\right)=0$$

имеет хотя бы одно решение, удовлетворяющее неравенству $$x(x-1)<0$$

Склад имеющий форму прямоугольного параллелепипеда $$ABCDA_1B_1C_1D_1$$ размером $$p\times n\times k$$ м$$^{3}$$ $$(p,n,k\in N)$$, плотно заставлен канистрами размером $$1\times 1\times 1$$ м$${}^{3}$$. Пуля летит по прямой и повреждает канистру только, если делает в ней две дырки. Возможно ли одним выстрелом повредить более чем $$\left(p+n+k-3\right)$$ канистр, если

а) $$p=5,n=3,k=2$$ и выстрел произведен по диагонали $$AC_1$$

б) $$p=26,n=13,k=5$$ и выстрел произведен по диагонали $$AC_1$$

в) Сколько канистр повредит пуля, пролетающая по диагонали $$AC_1$$, если $$p=1812,n=1914,k=1941$$