382 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
ОДЗ:
$$x−2>0, x−2≠1,$$
$$2x^2−12x+19>0$$
Решаем само уравнение:
$$2x^2−12x+19=(x−2)^2$$
$$x^2−8x+15=0$$
$$x=3$$ – не подходит под ОДЗ
$$x=5$$
Задание 2
Взрослые женщины составляют:
$$100\%−48\%=52\%$$
Женщины пенсионеры составляют:
$$0,15\cdot0,52=7,8\%$$%
Мужчины пенсионеры:
$$12,6\%−7,8\%=4,8\%$$ от всего населения
Всевозможные исходы – это 48% взрослые мужчины
$$P(A)=\frac{4,8}{48}=0,1$$
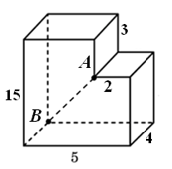
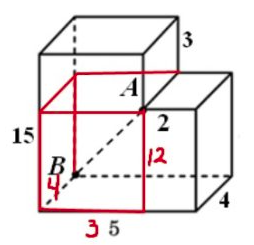
Задание 3
Вписать можно только равнобокую трапецию.
Значит $$DC=AB\Rightarrow$$ дуги DC и AB, отсекаемые хордами, тоже равны.
Каждая: $$\frac{360^{\circ}-(39^{\circ}+93^{\circ})}{2}=114^{\circ}$$
Тогда $$\angle ADB=\frac{114^{\circ}}{2}=57^{\circ}$$
Задание 4
По формулам приведения
$$−5\sinβ−11\sinβ$$
Подставляя известное значение получаем ответ $$-1,6$$
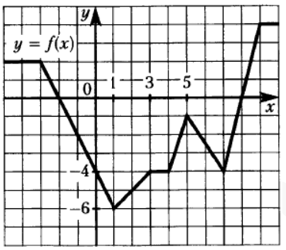
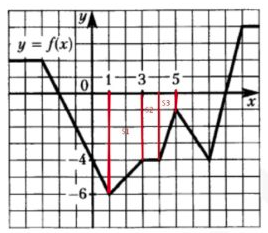
Задание 6
$$F(5)−F(1)=\int^5_1f(x)dx$$
Для этого посчитаем площади фигур:
$$S_1=\frac{4+6}{2}\cdot2=10$$
$$S_2=4\cdot1=4$$
$$S_3=\frac{1+4}{2}\cdot1=2,5$$
$$F(5)−F(1)=−(S_1+S_2+S_3)=−16,5$$
Задание 7
$$1,4+9t−5t^2\geq3$$
$$t\in [\frac{1}{5};\frac{8}{5}]$$
$$\tau=\frac{8}{5}−\frac{1}{5}=1,4$$
Задание 8
Пусть изначальный капитал $$x$$
Но обычно в таких задачах удобнее всего взять за $$x$$ какое-то хорошее число, чтобы было удобно работать с процентами, это никем не запрещается в первой части
Возьмем например $$x=100$$ рублей
Тогда $$50$$ рублей фирма вложила в квартиры
$$50\cdot0,6=30$$ – в дачные участки
$$50−30=20$$ – в банк под 5% годовых
Через год фирма получила 22% прибыли, т.е получила $$100\cdot1,22=122$$ рубля
Известно, получили от дачных участков $$30\cdot1,2=36$$
Получили от банка $$20\cdot1,05=21$$
Значит получили от квартир $$122−36−21=65$$
Прибыль от квартир $$65−50=15$$ (т.к мы вложили 50 рублей)
$$\frac{15}{50}=30\%$$
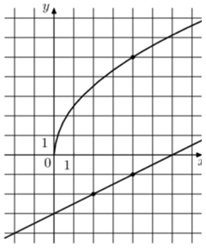
Задание 9
Подставляя отмеченные точки:
$$5=a\sqrt{4}$$
$$−2=k\cdot2+b$$
$$−1=k\cdot4+b$$
$$g(x)=0.5x−3$$
$$f(x)=2,5\sqrt{x}$$
Найдем точку пересечения
$$0,5x−3=2,5\sqrt{x}$$
$$x=36$$ – абцисса
$$f(36)=g(36)=2,5\cdot6=15$$ ордината
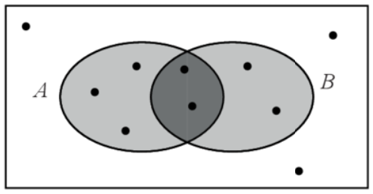
Задание 10
$$P(B|A)=\frac{P(BA)}{P(A)}$$ – по определению
$$P(A)=\frac{5}{10}$$ (всего 10 точек, 5 точек лежат в левом круге, т.е принадлежат событию А)
$$P(BA)=\frac{2}{10}$$ (всего 2 точки принадлежат пересечению двух кругов)
$$P(B|A)=\frac{\frac{2}{10}}{\frac{5}{10}}=\frac{2}{5}=0,4$$
Задание 11
Найдем критические точки:
$$\frac{1}{2\sqrt{x}}(6−\sqrt{x})+\sqrt{x}(−\frac{1}{2\sqrt{x}})=0$$
$$x=9$$ – т максимума по методу интервалов
$$f(9)=−27$$