381 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$7^{20x+16}=7\cdot10^{20x+15}$$
$$7^{20x+15}=10^{20x+15}$$
$$(\frac{7}{10})^{20x+15}=1$$
$$20x+15=0$$
$$x=−0,75$$
Задание 2
По формуле геометрической вероятности
$$P=\frac{|A|}{|Ω|},$$ где
$$A=[−3,8;0]$$
$$Ω=[−3,8;4,2]$$
$$|A|=3,8$$ – длина отрезка $$[-3.8;0]$$
$$|Ω|=8$$ – длина отрезка $$[-3.8;4.2]$$
$$P=\frac{3,8}{8}=0,475$$
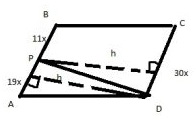
Задание 3
$$S_{BCDP}=\frac{11x+30x}{2}\cdot h=131,2$$
$$h=\frac{131,2\cdot2}{41x}=\frac{6,4}{x}$$
$$S_{APD}=\frac{1}{2}19xh$$
Подставляя, получаем ответ
Задание 4
$$\cos\frac{\pi}{33}\cos\frac{2\pi}{33}\cos\frac{4\pi}{33}\cos\frac{8\pi}{33}\cos\frac{16\pi}{33}=$$
$$=\frac{1}{\sin\frac{\pi}{33}}\cdot\sin\frac{\pi}{33}\cos\frac{\pi}{33}\cos\frac{2\pi}{33}\cos\frac{4\pi}{33}\cos\frac{8\pi}{33}\cos\frac{16\pi}{33}=$$
$$=\frac{1}{\sin\frac{\pi}{33}}\frac{1}{2}\sin\frac{2\pi}{33}\cos\frac{2\pi}{33}\cos\frac{4\pi}{33}\cos\frac{8\pi}{33}\cos\frac{16\pi}{33}=$$
$$=\frac{1}{\sin\frac{\pi}{33}}\frac{1}{4}\sin\frac{4\pi}{33}\cos\frac{4\pi}{33}\cos\frac{8\pi}{33}\cos\frac{16\pi}{33}=$$
$$=\frac{1}{\sin\frac{\pi}{33}}\frac{1}{8}\sin\frac{8\pi}{33}\cos\frac{8\pi}{33}\cos\frac{16\pi}{33}=$$
$$=\frac{1}{\sin\frac{\pi}{33}}\frac{1}{16}\sin\frac{16\pi}{33}\cos\frac{16\pi}{33}=$$
$$=\frac{1}{\sin\frac{\pi}{33}}\frac{1}{32}\sin\frac{32\pi}{33}=\frac{1}{\sin\frac{\pi}{33}}\frac{1}{32}\sin(\pi-\frac{\pi}{33})=$$
$$=\frac{1}{\sin\frac{\pi}{33}}\frac{1}{32}\sin\frac{\pi}{33}=\frac{1}{32}=0,03125$$
Задание 5
$$\frac{V_{куб}}{V_{п-да}}=\frac{S_{куб}}{S_{п-да}}$$
$$\frac{V_{куб}}{S_{куб}}=\frac{V_{п-да}}{S_{п-да}}$$
$$\frac{V_{куб}}{S_{куб}}=\frac{a^3}{6a^2}=\frac{a}{6}$$
$$\frac{V_{п-да}}{S_{п-да}}=\frac{2\cdot3\cdot6}{2(6+18+12)}=\frac{1}{2}$$
$$\frac{a}{6}=\frac{1}{2}$$
$$a=3$$
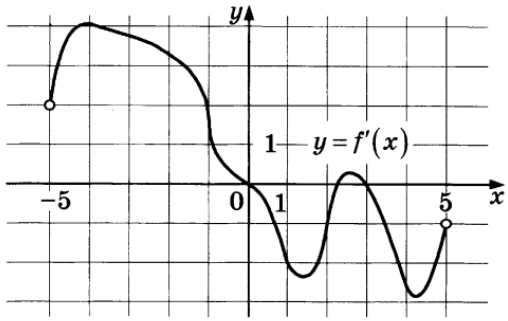
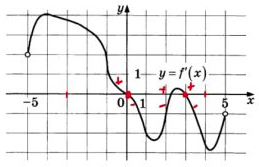
Задание 7
$$3,2\sin\pi t\geq1,6$$
$$\sin\pi t\geq0,5$$
$$\frac{\pi}{6}+2\pi n\leq\pi t\leq\frac{5\pi}{6}+2\pi n$$
так как просят в течении первой секунды, то $$n=0$$
$$\frac{1}{6}\leq t\leq\frac{5}{6}$$
$$\tau=\frac{\frac{5}{6}−\frac{1}{6}}{1}=\frac{2}{3}\approx0,67$$
Задание 8
Составим систему исходя из условия, не забывая переводить минуты в часы
$$\frac{S}{V_т}=\frac{S}{V_п}+\frac{16}{5}$$
$$\frac{S}{V_т}=\frac{S+288}{V_п}$$
$$\frac{S}{V_т+10}=\frac{S}{V_п+10}+2,4$$
Решаем систему и получаем ответ $$360$$
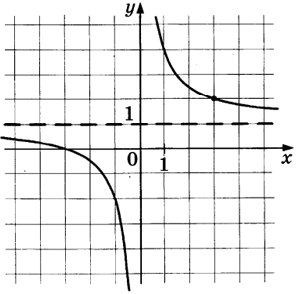
Задание 9
$$2=\frac{k}{3}+a$$
$$−2=\frac{k}{-1}+a$$
Решая систему, получаем:
$$f(x)=\frac{3}{x}+1$$
$$f(-12)=0,75$$
Задание 10
Нас устраивает: утро ясное дождя не будет или утро облачное и дождя не будет
$$P(A)=0,6\cdot(1−0,3)+0,4\cdot(1-0,95)=0,44$$
Задание 11
$$y=\frac{2\sin x\cos x}{\frac{\sqrt{2}}{2}(\cos x+\sin x)}=\frac{4}{\sqrt{2}\cdot\frac{\sin x}{1+\tg x}}$$
$$y'=\frac{\cos x(1+\tg x)−\sin x\frac{1}{\cos^2x}}{(1+\tg x)^2}=0$$
$$\cos x(1+\tg x)-\sin x\frac{1}{\cos^2 x}$$
$$\cos x(1+\tg x)-\sin x(1+\tg^2 x)=0$$
$$\cos x(1+\tg x)=\sin x(1+\tg^2 x)$$
$$1+\tg x=\tg x(1+tg^2x)$$
$$1+\tg x=\tg x+\tg^3x$$
$$\tg^3x=1$$
$$\tg x=1$$
$$x=\frac{\pi}{4}$$ – точка экстремума
$$y(0)=0$$
$$y(\frac{\pi}{4})=1$$
$$y(\frac{\pi}{2})=0$$