367 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
ОДЗ:
$$0\leq x\leq\frac{3}{2}$$
$$x^2=3$$
$$x=3$$ - не подходит под ОДЗ
$$x=−3$$ – не подходит под ОДЗ
$$\sqrt{3-2x}=x$$
$$x^2+2x−3=0$$ (возвели в квадрат)
$$x=1$$ – подходит
$$x=−3$$ – не подходит под ОДЗ
Задание 2
Пусть Михаил попадет в какую-то из групп (неважно в какую), тогда для Олега останется только 1 место в этой группе, а всего мест 5 (т.к Михаил свое занял)
$$P(A)=\frac{1}{5}=0,2$$
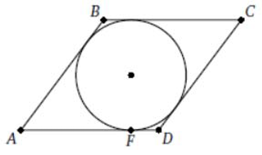
Задание 3
Треугольник AOD – прямоугольный, OF – высота в прямоугольном треугольнике, значит
$$OF^2=AF\cdot FD=4x\cdot x=4x^2$$
$$OF=2x$$
$$AO=\sqrt{16x^2+4x^2}=2\sqrt{5}x$$
$$\cos\alpha=\frac{4x}{2\sqrt{5}x}=\frac{2}{\sqrt{5}}$$
$$\cos2\alpha=2\cos^2\alpha-1=0,6$$
Задание 4
$$\frac{5\cdot2\sin49^{\circ}\cos49^{\circ}}{\sin49^{\circ}\cdot\sin41^{\circ}}=\frac{10\cos(90^{\circ}-41^{\circ})}{\sin41^{\circ}}=10$$
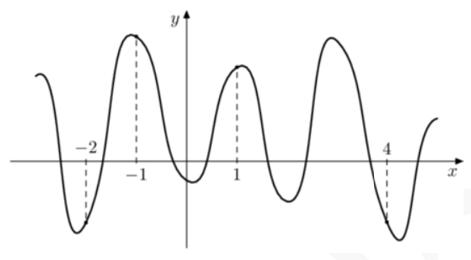
Задание 6
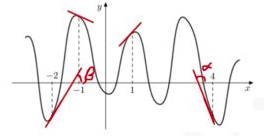
По геометрическому смыслу производной $$f'(x_0)=\tg\alpha$$
Видно, что в точках $$x=−2;4$$ функция убывает, значит $$f'(x=−2;4)<0.$$
Из рисунка видно, что в точке $$x=4$$ тангенс угла больше чем в точке $$x=-2,$$ значит, значение будет наименьшим именно в точке $$x=4.$$
Задание 7
Нужно решить неравенство
$$2\cdot\cos(240^{\circ}t−120^{\circ})\geq1$$
$$\cos(240^{\circ}t-120^{\circ})\geq0,5$$
$$-\frac{\pi}{3}+2\pi n\leq240^{\circ}t-120^{\circ}\leq\frac{\pi}{3}+2\pi n$$
$$-60^{\circ}+360^{\circ}n\leq240^{\circ}t-120^{\circ}\leq60^{\circ}+360n$$
$$60^{\circ}+360^{\circ}n\leq240^{\circ}t\leq180^{\circ}+360^{\circ}n$$
$$\frac{1}{4}+1,5n\leq t\leq\frac{3}{4}+1,5n$$
$$n=0$$
$$\frac{1}{4}\leq t\leq\frac{3}{4}$$
Значит на протяжении первой секунды лампа будет гореть $$\frac{3}{4}-\frac{1}{4}=0,5$$ или $$50\%$$
Задание 8
Пусть $$x$$ – скорость грибника, тогда
$$1,25x$$ – скорость туриста
$$1,25\cdot1,6x=2x$$ – скорость спортсмена
$$S=xt_1$$
$$S=1,25xt_2$$
$$t_1−t_2=1$$
$$\frac{S}{x}=5=t_1$$ – это и есть время $$t_1$$ (за сколько дошел грибник до B)
Значит, $$t_2=t_1−1=4$$
$$S=2x\cdot t_3$$
$$t_3=\frac{S}{2x}=\frac{5}{2}=2,5$$
Но так как спортсмен вышел через два часа, то $$dt_3=2,5-2=0,5$$ часа или $$30$$ минут
Задание 9
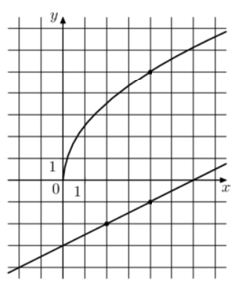
Угловой коэффициент прямой легко найти через тангенс $$\tg\alpha=k=0,5$$
$$b=−3$$
$$5\cdot a\cdot\sqrt{4},$$ откуда $$a=2,5$$
Теперь найдем точки пересечения:
$$2,5\sqrt{x}=0,5x-3$$ – решаем уравнение
$$x=36$$
$$f(36)=15$$
Задание 10
Так как всего в турнире 16 игроков и каждая команда из 2 человек, тогда в каждом туре участвуют:
1) 16 человек
2) 8 человек
3) 4 человека
4) 2 человека
Тогда благоприятные события:
$$A_1$$ – они попадутся в 1-ом туре $$P(A_1)=\frac{1}{15}$$
$$A_2$$ – не играли в 1-ом туре, но попались во втором, т.е. оба матча в 1-ом туре они выиграли
$$P(A_2)=\frac{14}{15}\cdot0,5\cdot0,5\cdot\frac{1}{7}=\frac{1}{30}$$
$$A_3$$ – не играли в 1-ом туре и во 2-ом туре, но попались в 3-ем туре, т.е. они выиграли предыдущие два тура
$$P(A_3)=\frac{14}{15}\cdot0,5\cdot0,5\cdot\frac{6}{7}\cdot0,5\cdot0,5\cdot\frac{1}{3}=\frac{1}{60}$$
$$A_4$$ – встретились в 4-ом туре, выиграли предыдущие 3 тура
$$P(A_4)=\frac{14}{15}\cdot0,5\cdot0,5\cdot\frac{6}{7}\cdot0,5\cdot0,5\cdot\frac{2}{3}\cdot0,5\cdot0,5\cdot1=\frac{1}{120}$$
$$P_{иск}(A_1+A_2+A_3+A_4)=P(A_1)+P(A_2)+P(A_3)+P(A_4)=0,125$$
Задание 11
$$y=\frac{2}{\sqrt{(x+1)^2+4}}$$
Нужно найти наибольшее значение функции, значит, знаменатель должен принимать наименьшее значение
$$\sqrt{(x+1)^2+4}\quad min?$$
Очевидно, что выражение будет минимально, когда $$(x+1)^2=0$$
$$x=−1$$
$$y(−1)=1$$
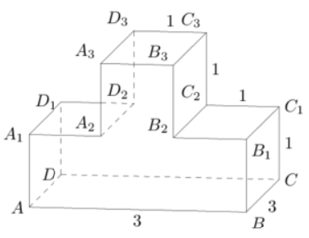
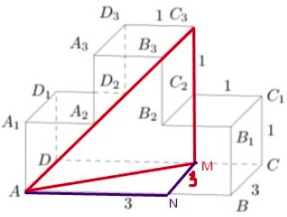
Задание 13
А) Найдите угол между плоскостью сечения и плоскостью BCC1
Б) Найдите объем пирамиды, основанием которой является сечение куба, а вершиной - точка D.