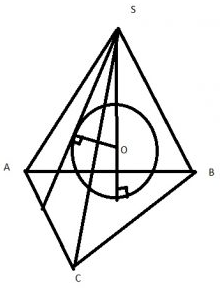343 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Больше разборов на моем ютуб-канале
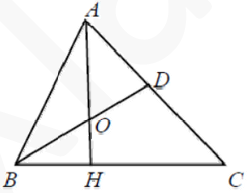
Задание 2
$$31-19=12$$
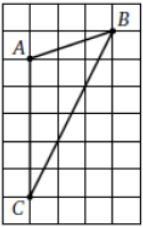
Задание 3
$$\tgβ=\frac{1}{2}$$
$$\tgα=\frac{1}{3}$$
$$\tg(α+β)=\frac{\tgα+\tgβ}{1-\tgα\cdot\tgβ}=$$1 или $$α+β=45°$$
Но $$∠A=90+∠α$$
Значит,
$$∠A+∠B=90+45=135$$
Задание 4
(Автор задачи Николай Журавлев)
Всего свободных мест для Дании 7 (Швеция и Норвегия свои места заняла по условию)
Места после Швеции и Норвегии – это 8,9 места (т.е. 2 благоприятных для нас места)
$$P(A)=\frac{2}{7}\approx0,29$$
Задание 5
Замена $$\sqrt{x^2+11}=t$$, $$t\geq0$$
$$t^2+t=42$$
$$t=−7$$ – не подходит
$$t=6$$
$$\sqrt{x^2+11}=6$$
$$x^2+11=36$$ (можно смело возводить в квадрат никакого ОДЗ не надо, т.к по условию уже корень положительный и равен $$6>0$$)
$$x=\pm5$$
$$-5+5=0$$
Задание 7
По физическому смыслу производной
$$a=x''(t)=2t−2$$
$$2t−2=0$$
$$t=1$$
Т.е. через 1 секунду после начала движения ускорение будет $$= 0$$
Задание 8
Знатоки стереометрии сразу вспомнят формулу $$S_{п.п}=\frac{3V}{R}$$, где $$R$$ – радиус вписанной сферы.
Но мы ее попробуем вывести.
$$V=\frac{1}{3}S_{осн}\cdot h$$
Если обозначить за т. O – центр вписанной сферы,
$$V=V_{OABC}+V_{OASC}+V_{OBSC}+V_{OASB}$$
$$V_{OABC}=\frac{1}{3}S_{ABC}\cdot R$$
$$V_{OASC}=\frac{1}{3}S_{ASC}\cdot R$$
$$V_{OBSC}=\frac{1}{3}S_{BSC}\cdot R$$
$$V_{OASB}=\frac{1}{3}S_{ASB}\cdot R$$
$$V=\frac{1}{3}R\cdot S_{полн.п}$$
$$S_{полн.п}=\frac{3\cdot3}{1}=9$$
Задание 9
$$\ln2\cdot\log_2e^{1/3}=\ln2\cdot\frac{\ln e^{1/3}}{\ln2}=\frac{1}{3}$$
$$\log_{\frac{1}{3}}9^{1/6}=-\frac{1}{3}$$
$$8^{-1/3}=0,5$$
Задание 10
$$\frac{100}{0,8}\cdot\ctg α\leq125$$
$$\ctg α\leq1$$
Т.к. угол острый, на $$[0;\frac{\pi}{2}]$$ котангенс убывает, значит минимальный угол будет при $$\ctg α=1$$
$$α=45$$
Задание 11
Задание 12
Т.к все функции возрастающие и $$x^2-2x+4$$ – ветви вверх, то минимум будет в вершине параболы
$$x_0=-\frac{-2}{2}=1$$
$$y(1)=2^{\log_3 3}=2$$
Задание 13
Задание 14
Задание 16
Задание 17
Задание 19
Б) Может ли быть ровно 15 зелёных карточек?
В) Какое наибольшее количество жёлтых карточек может быть?