373 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
Пусть $$\sqrt{\frac{x}{4}-2}=t, t\geq0$$
Тогда получим уравнение:
$$t+\frac{\sqrt{29}}{2}=2t$$
$$t=\frac{\sqrt{29}}{2}$$
Обратная замена
$$\sqrt{\frac{x}{4}-2}=\frac{\sqrt{29}}{2}$$
Возводим в квадрат, можно спокойно это делать, т.к $$\frac{\sqrt{29}}{2}>0$$
И находим чему равно x
$$x=37$$
Задание 2
Нас устраивает два исхода:
Вытягиваем оба разную красную пуговицу или оба раза синию
$$P(A+B)=\frac{10}{16}\cdot\frac{9}{15}+\frac{6}{16}\cdot\frac{5}{15}=0,5$$
Задание 3
Так как трапеция равнобедренная, то $$AH_1=BH_2=1, H_1H_2=BC=4$$
По теореме Пифагора $$CH_2=BH_2=\sqrt{25−1}=\sqrt{24}$$
$$AC=BD=\sqrt{24+25}=7$$
Задание 4
Используем формулу:
$$\cos\alpha+\cos\beta=2\cos(\frac{\alpha+\beta}{2})\cos(\frac{\alpha-\beta}{2})$$ и
$$\cos\alpha-\cos\beta=-2\sin(\frac{\alpha+\beta}{2})\sin(\frac{\alpha-\beta}{2})$$
$$\cos\alpha\sin\beta=0,5(\sin(\alpha+\beta)-\sin(\alpha+beta))$$
Тогда
$$\cos10\cdot\cos10-\cos100\cdot\sin170$$
$$\cos^2 10=\frac{1+\cos20}{2}$$
$$\cos100\cdot\sin170=0,5(\sin270-\sin(-70))=0,5(\sin(360-90)+\sin70)=$$
$$=0,5(-1+\sin70)=0,5(-1+\sin(90-20))=0,5(-1+\cos20)$$
Итого
$$\frac{1+\cos20}{2}−\frac{−1+\cos20}{2}=1$$
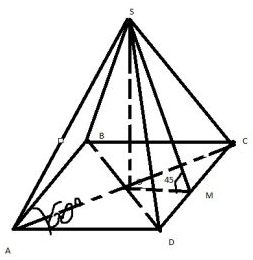
Задание 5
$$V=\frac{1}{3}S_{осн}\cdot SO$$
$$S_{осн}=8^2\sin60=32\sqrt{3}$$
С другой стороны $$S=2\cdot a\cdot r,$$ где r – радиус вписанной окружности, т.е OM, откуда
$$OM=\frac{S}{2a}=2\sqrt{3}$$
$$V=64$$
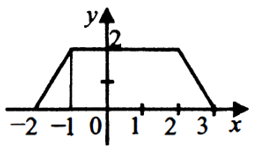
Задание 6
$$F(3)-F(-1)=\int_{-1}^{3}f(x)dx$$
Или это будет площадь прямоугольной трапеции
$$S_{трап}=\frac{3+4}{2}\cdot2=7$$
Задание 7
Найдём время полёта:
$$6 + 9,5t - 5t^2=0$$
$$x=-0,5$$ - не может быть отрицательно
$$x=\frac{12}{5}=2,4$$
Теперь
$$6 + 9,5t - 5t^2\leq7,7$$
$$0<t<0,2$$
$$t\geq1,7$$
Время полета на высоте не более 1,54 м равно $$(0,2-0)+(2,4-1,7)=0,2+0,7=0,9$$
$$\frac{0,9}{2,4}\cdot100=37,5\%$$
Задание 8
Пусть $$x$$ – скорость третьей машины
Пусть $$t$$ – время встречи третьего автомобиля со вторым (у к-го скорость 40 км\ч)
Тогда можно составить два уравнения
$$\left\{\begin{matrix} tx=(t+0,5)\cdot40\\ (t+1,5)\cdot x=(t+2)\cdot50 \end{matrix}\right.$$
Решая систему:
$$x=60$$
Задание 9
По картинке, очевидно, что $$a=1$$
Осталось только подставить две отмеченные точки в уравнение и получить
$$g(x)=x^2−2x−1$$
$$x^2−2x−1=2x^2+11x+11$$
$$x=−12$$
$$x=−1$$
$$y=g(−12)=167$$
Задание 10
$$A$$ – сдал 1,2 экзамен
$$B$$ – сдал 1,3 экзамен
$$C$$ – сдал 2,3 экзамен
$$D$$ – сдал все экзамены
Исходная вероятность будет равна сумме вероятности этих несовместных событий:
$$P=0,9\cdot0,9\cdot0,2+0,9\cdot0,1\cdot0,8+0,1\cdot0,9\cdot0,9+0,9\cdot0,9\cdot0,8=0,954$$
Задание 11
Найдем критические точки
$$y'=0$$
$$4e^{4x}−4e^x=0$$
$$e^x(4e^{3x}−4)=0$$
$$e^x=0$$ – нет решений, т.к $$e^x>0$$
$$e^{3x}=1$$
$$3x=0$$
$$x=0$$
$$y(0)=1−4+8=5$$ по методу интервалов это и есть наименьшее значение