254 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 254 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №254 (alexlarin.com)
Решаем ЕГЭ 254 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №254 (alexlarin.com)
Задание 2
На рисунке изображен график осадков в г.Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм. Определите по рисунку, сколько дней из данного периода выпадало от 2 до 8 мм осадков.
Выпадало от 2 до 8 мм осадков 7,8,9 февраля, то есть 3 дня
Задание 3
Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
$$OB=\sqrt{(8-0)^{2}+(2-0)^{2}}=\sqrt{68}$$
$$AB=\sqrt{(10-8)^{2}+(2-8)^{2}}=\sqrt{40}$$
$$AC=\sqrt{(2-10)^{2}+(6-8)^{2}}=\sqrt{69}$$
$$OC=\sqrt{(2-0)^{2}+(6-0)^{2}}=\sqrt{40}$$
Получили параллелограм. Его диагонали точкой пересечения делятся пополам, тогда: Тогда : $$M_{y}=\frac{A_{y}+O_{y}}{2}=\frac{8+0}{2}=4$$
Задание 4
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 7 октября погода в Волшебной стране хорошая. Найдите вероятность того, что 10 октября в Волшебной стране будет отличная погода.
Вероятность смены погоды : $$1-0,8=0,2$$. Рассмотрим возможные исходы, когда 7 была хорошая (X), а 10 - отличная погода (O):
| Число / исход | 7 | 8 | 9 | 10 | вероятность |
| 1 исход | X | X | X | O | 0,8*0,8*0,2 |
| 2 исход | X | X | O | O | 0,8*0,2*0,8 |
| 3 исход | X | O | X | O | 0,2*0,2*0,2 |
| 4 исход | X | O | O | O | 0,2*0,8*0,8 |
Вероятность данного события: $$P=3*0,8^{2}*0,2+0,2^{3}=0,384+0,008=0,392$$
Задание 5
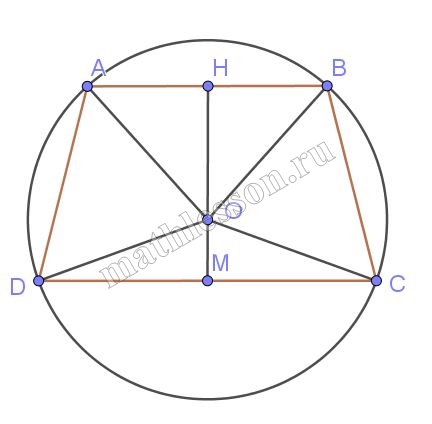
Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Из $$\Delta HBO$$ (OH-высота): $$OH=\sqrt{OB^{2}-HB^{2}}=\sqrt{5^{2}-3^{2}}=4$$
Из $$\Delta OMC$$ (OM-высота): $$OM=\sqrt{OC^{2}-MC^{2}}=\sqrt{5^{2}-4^{2}}=3$$
$$HM=4+3=7$$
Задание 6
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x)$$, определенной на интервале (‐3;14). Найдите промежутки убывания функции $$f(x)$$. В ответе укажите длину наибольшего из них.
Функция убывает там, где $${f}’ (x)<0$$. Убывает на промежутке: (-4;-3) - длина 1; (2;6) - длина 4; (11;13) - длина 2
Задание 7
Рассмотрим куб со стороной 3 и параллели 1;5;5 . Если из их площади поверхности вычесть 2 раза по 3*3 , то получим площадь поверхности исходной фигуры: $$S=3*3*6+1*5*2+1*5*2+5*5*2-3*3*2=106$$
Задание 8
Найдите значение выражения $$\frac{-19\sin 94^{\circ}}{\sin 47^{\circ}\sin 43^{\circ}}$$
$$\frac{-19 \sin 94}{\sin 47 \sin 43}=$$$$\frac{-38 \sin 47 \cos 47}{\sin 47 \sin (90-47)}=$$$$\frac{-38 \cos 47}{\cos 47}=-38$$
Задание 9
Независимое агентство намерено ввести рейтинг новостных интернет‐изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5‐балльной шкале целыми числами от 0 до 4. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится вдвое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид $$R=\frac{5In+Op+2Tr+Q}{A}$$ Если по всем четырем показателям какое‐то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.
Пусть по всем показателям оценка 4, тогда и рейтинг равен 4. $$A=\frac{5 I_{n}+O_{p}+2I_{r}+Q}{R}=$$$$\frac{5*4+4+2*4+4}{4}=9$$
Задание 10
Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?
Раз прибыль составляет 200% (400%) от предыдущего капитала, то сам капитал увеличивался в 3 (5) раз в соответствии с предыдущим годом . Т.е. имеем геометрические прогрессии с $$q_{1} =3$$; $$q_{2}=5$$; $$n_{1}=2006-2000=6$$; $$n_{2 }=2006-2002=4$$ .(вычитается на 1 год раньше , так как первый год учитывался и является первым членом геометрической прогрессии)
Тогда: $$b_{6}=5000*3^{6-1}=1215000$$(Альфа)
$$b_{4}=1000*5^{4-1}=1250000$$(Бета)
Разница в капитале : $$1250000-1215000=35000$$
Задание 11
Найдите наибольшее значение функции $$y=12\sin x -6\sqrt{3}x+\sqrt{3}\pi+6$$ на отрезке $$[0;\frac{\pi}{2}]$$ .
Найдем производную : $${y}'=12 \cos x-6\sqrt{3}$$
Приравняем к 0: $$12 \cos x=6\sqrt{3}\Leftrightarrow$$ $$\cos x=\frac{\sqrt{3}}{2}\Leftrightarrow$$ $$\pm \frac{\pi}{6}+2 \pi n , n \in Z$$
Как видим $$\frac{\pi}{6}$$ - точка максимума, тогда:
$$y_{max}=y(\frac{\pi}{6})=$$$$12 *\frac{1}{2}-6\sqrt{3}*\frac{\pi}{6}+\sqrt{3} \pi +6 =12$$
Задание 12
ОДЗ: $$1-\sin ^{2}x\geq 0\Leftrightarrow$$ $$\sin^{2}x\leq 1\Leftrightarrow$$ $$x \in R$$
$$\sqrt{1-\sin^{2}x}=\sqrt{\cos ^{2}x}=\left | \cos x \right |$$
$$3*2^{\cos x+3 \left | \cos x \right |}+11*2^{2 \cos x}-34=0$$
1) Если $$\cos \geq 0$$, то $$3*2^{4 \cos x}+11*2^{2 \cos x}-34=0\Leftrightarrow$$$$3*4^{2 \cos x}+1*4^{\cos x}-34=0$$
Пусть $$4^{\cos x}=t>0$$
$$3t^{2}+11t-34=0$$
$$D=121+408=529$$
$$t_{1}=\frac{-11+23}{6}=2$$
$$t_{2}=\frac{-11-23}{6}<0$$
Тогда $$4^{\cos x}=2\Leftrightarrow$$ $$\cos x=\frac{1}{2}\Leftrightarrow$$ $$x=\pm \frac{\pi}{3}+2 \pi n , n \in Z$$
2) Если $$\cos x <0$$, тогда : $$3*2^{-2 \cos x}+11*2^{2 \cos x}-34=0$$
Пусть $$2^{2 \cos x}=t>0$$
$$3*\frac{1}{t}+11t-34=0\Leftrightarrow$$ $$\frac{11t^{2}-34t+3}{t}=0\Leftrightarrow$$ $$11t^{2}-34t+3=0$$
$$D=1156-132=1024$$
$$t_{1}=\frac{34+32}{22}=3$$
$$t_{2}=\frac{34-32}{22}=\frac{1}{11}$$
Тогда $$2^{2 \cos x}=3\Leftrightarrow$$ $$4^{\cos x}=3\Leftrightarrow$$ $$\cos x=log_{4}3>0\Rightarrow$$ не подходит
$$2^{2 \cos x}=\frac{1}{11}\Leftrightarrow$$ $$4^{\cos x}=\frac{1}{11}\Leftrightarrow$$ $$\cos x=\log_{4}\frac{1}{11}<-1$$ - не подходит (так как $$\log_{4}\frac{1}{11}<\log_{4}\frac{1}{4}=-1$$) - решений нет
Б) На промежутке $$[-\frac{3 \pi}{2}; \frac{\pi}{2}]$$
$$\frac{\pi}{3}+2 \pi n , n \in Z: \frac{\pi}{3}$$
$$-\frac{\pi}{3}+2 \pi n ,n \in Z: -\frac{\pi}{3}$$
Задание 13
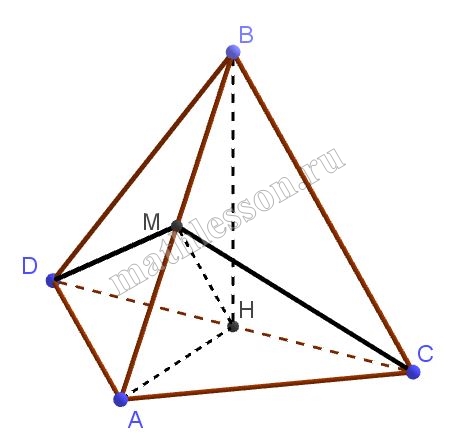
В треугольной пирамиде ABCD ребра АВ и CD взаимно перпендикулярны, AD=BC, 4 , $$\angle DAC=\frac{\pi}{2},\angle ACD=\frac{\pi}{4}$$ , угол между ребром DC и гранью АВС равен $$\frac{\pi}{6}$$.
A) 1) $$\angle ACD=\frac{\pi}{4}$$; $$\angle A=\frac{\pi}{2}\Rightarrow$$ $$\angle ADC=\frac{\pi}{4}\Rightarrow$$ $$AD=AC$$
2) Пусть AH-проекция AB на $$(ACD)\Rightarrow$$ по теореме о трех перпендикулярах $$AH\perp CD$$, тогда $$\Delta ADH=\Delta AHC$$(по гипотенузе и катету )$$\Rightarrow DH=HC\Rightarrow$$ BH-медиана
3) $$AB\perp DC$$ и $$AH\perp CD\Rightarrow$$ $$(ABH)\perp CD\Rightarrow$$ $$BH\perp CD$$ , но тогда BH-высота $$\Rightarrow \Delta DBC$$ –равнобедренный и $$DB=BC$$
4) $$AD=AC=CB=DB\Rightarrow$$ $$\Delta DBC=\Delta DAC$$ (DC-общая, $$\angle DBC=90$$)
5) $$OM\perp AB$$, $$CD\perp AB\Rightarrow$$ $$(DMC)\perp AB\Rightarrow$$ $$\angle DCM=\frac{\pi}{6}$$
6) $$CM=DM$$(высота в равных треугольниках ) $$\Rightarrow$$ $$\Delta DMC$$ - равнобедренный $$\Rightarrow$$ MH-медиана и высота (т.к. $$(AHB)\perp CD$$ и DH=HC). Следовательно, точка располагается на биссектрисе угла, потому она равноудалена от его сторон
Б) 1) Пусть $$AC=x\Rightarrow$$ $$\Delta ACD$$ : $$CD=x\sqrt{2}$$$$\Rightarrow$$ $$HC=\frac{x\sqrt{2}}{2}$$. Из $$\Delta MHC$$: $$MH=HC*tgC=\frac{x\sqrt{2}}{2}*\frac{\sqrt{3}}{3}=\frac{x\sqrt{6}}{6}$$
2) $$\Delta AHM$$ – прямоугольный , $$AH=HC=\frac{x\sqrt{2}}{2}$$. $$\sin \angle MAN=\frac{MH}{AH}=$$$$\frac{x\sqrt{6}}{6}*\frac{\sqrt{2}}{x\sqrt{2}}=$$$$\frac{\sqrt{3}}{3}$$$$\Rightarrow$$ $$\angle MAH=\arcsin \frac{\sqrt{3}}{3}$$
Задание 14
Решите неравенство $$(\sqrt{2}+1)^{\frac{6x-6}{x+1}}\leq (\sqrt{2}-1)^{-x}$$
ОДЗ: $$x+1\neq 0\Leftrightarrow$$ $$x\neq -1$$
Рассмотрим правую часть неравенства : $$(\sqrt{2}-1)^{-x}=(\frac{1}{\sqrt{2}-1})^{x}|:(\sqrt{2}+1)^{x}\Rightarrow$$ $$\frac{(\sqrt{2}+1)^{x}}{((\sqrt{2}-1)(\sqrt{2}+1))^{x}}=$$$$\frac{(\sqrt{2}+1)^{x}}{1^{x}}=(\sqrt{2}+1)^{x}$$
Неравенство примет вид: $$(\sqrt{2}+1)^{\frac{6x-6}{x+1}}\leq (\sqrt{2}+1)^{x}\Leftrightarrow$$ $$\frac{6x-6}{x+1}\leq x\Leftrightarrow$$ $$\frac{6x-6-x^{2-x}}{x+1}\leq 0\Leftrightarrow$$ $$\frac{x^{2}-5x+6}{x+1}\geq 0\Leftrightarrow$$ $$\frac{(x-2)(x-3)}{x+1}\geq 0\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}x>-1\\x\leq 2\end{matrix}\right.\\x\geq 3\end{matrix}\right.$$
Задание 15
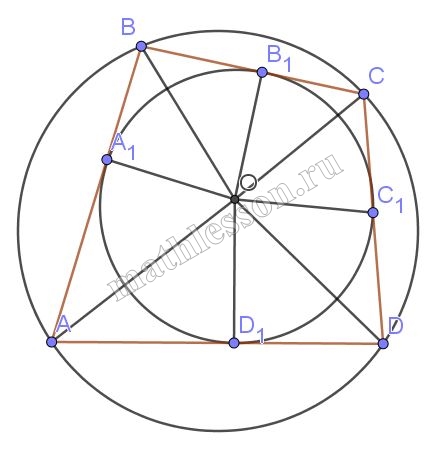
Четырехугольник, один из углов которого равен $$arccos(\frac{3}{5})$$ , вписан в окружность радиуса $$2\sqrt{10}$$ и описан около окружности радиуса 3.
A) 1) O- центр вписанной окружности . Пусть $$\angle BAD =2\alpha$$ $$\Rightarrow$$ $$\angle BCD=180-2\alpha$$ (свойство вписанного четырехугольника); $$\angle CDA=2\beta$$ $$\Rightarrow$$ $$\angle CBA=180-2\beta$$
2) $$AA_{1}=AD_{1}$$(свойство касательных ); $$OA_{1}\perp AB$$ ; $$OD_{1}\perp AD$$; $$OA$$ - общая $$\Rightarrow$$ $$\Delta A_{1}OA=\Delta OAD_{1}\Rightarrow$$ $$A_{1}AO=\angle OAD_{1}=\alpha$$
3) $$\angle B_{1}OC_{1}=180-\angle BCD=2\alpha$$$$\Rightarrow$$ $$\angle B_{1}OC=\angle COC_{1}=\alpha$$. Аналогично, $$\angle ODD_{1}=\angle ODC_{1}=\angle A_{1}OB=\angle BOB_{1}=\beta$$
4) Пусть $$\angle A=\arccos \frac{3}{5}\Rightarrow$$ $$\cos 2\alpha =\frac{3}{5}\Rightarrow$$ $$2\cos ^{2}\alpha -1=\frac{3}{5}\Rightarrow$$ $$2\cos ^{2}\alpha=\frac{8}{5}\Rightarrow$$ $$\cos ^{2}\alpha =\frac{4}{5}\Rightarrow$$ $$\sin^{2}\alpha =\frac{1}{5}$$,$$tg^{2}\alpha =\frac{1}{4}$$, $$ctg^{2}\alpha =4$$ т.к. $$\angle \alpha$$ - острый , то $$tg\alpha =\frac{1}{2}$$, $$ctg \alpha =2$$
5) $$S_{BA_{1}D}=\frac{1}{2}BA_{1}*A_{1}O$$; $$BA_{1}=\frac{1}{2}A_{1}O *tg\beta \Rightarrow$$ $$S_{BA_{1}O}=\frac{1}{2}*3*3*tg\beta \Rightarrow$$ $$S_{A_{1}OB_{1}B}=9tg\beta$$. Аналогично : $$S_{B_{1}OC_{1}C}=9tg\alpha$$; $$S_{A_{1}OD_{1}A}=2*\frac{1}{2}*AA_{1}*A_{1}O, A_{1}A=A_{1}O *ctg \alpha \Rightarrow$$ $$S_{A_{1}OD_{1}A}=9ctg \alpha$$ ; $$S_{DC_{1}OD_{1}}=9ctg \beta$$
$$S_{ABCD}=9(tg\alpha +tg \beta +ctg \alpha +ctg \beta )(1)$$
Пусть $$tg\beta =a; ctg\beta =b$$
6) $$AB=AA_{1}+A_{1}B=3 ctg \alpha +3 tg\beta =6+3a$$; $$AD=AD_{1}+D_{1}D=3ctg \alpha +3ctg \beta =6+3b$$
По т. Синусов из $$\Delta BAD$$ : $$BD^{2}=(3(a+2))^{2}+(3(b+2))^{2}-2*3(a+2)*3(b+2)*\cos 2\alpha =$$$$9((a+2)^{2}+(b+2)^{2}-2(a+2)(b+2)*\cos 2\alpha) =$$$$9(a^{2}+b^{2}+4(a+b)+8-\frac{6}{5}(4+2(a+b)+ab))$$
Т.к. $$ab=tg\beta *ctg \beta =1$$, то $$a^{2}+b^{2}=(a+b)^{2}-2ab=(a+b)^{2}-2$$ . Пусть $$a+b=x$$, то: $$BD^{2}=9(x^{2}-2+4x+8-\frac{6}{5}(5+2x))=(x^{2}+\frac{8}{5}x)*9(2)$$
С другой стороны , около $$\Delta ABD$$ описана окружность радиуса $$2\sqrt{10}$$, тогда: $$\frac{BD}{\sin 2\alpha }=4\sqrt{10}\Rightarrow$$ $$BD^{2}=16*10*\sin ^{2}2\alpha =160*\frac{16}{25}(3)$$
Из (2) и (3): $$9(x^{2}+\frac{8}{5}x)=160*\frac{16}{25}\Leftrightarrow$$ $$5*9x^{2}+72x=512\Leftrightarrow$$ $$45x^{2}+72x-512=0$$
$$D=5184+92160=97344=312^{2}$$
$$x_{1}=\frac{-72+312}{90}=\frac{240}{90}=\frac{8}{3}$$
$$x_{2}=\frac{-72-312}{90}=-\frac{64}{15}$$ ($$tg\beta +ctg\beta >0$$)
$$S=9(\frac{1}{2}+2+\frac{8}{3})=\frac{31}{6}*9=\frac{93}{2}$$
Б ) Пусть $$\varphi$$ - угол между BD и AC , тогда: $$S=\frac{1}{2} BD*AC* \sin \varphi \Rightarrow$$ $$\sin \varphi =\frac{2S}{BD*AC}$$
1) $$BD=\sqrt{9*(\frac{64}{9}+\frac{8}{5}*\frac{8}{3})}=$$$$\sqrt{\frac{512}{5}}=16\sqrt{\frac{2}{5}}$$
2) $$tg \beta +ctg\beta =\frac{8}{3}\Rightarrow$$ $$\frac{\sin \beta }{\cos \beta }+\frac{\cos \beta }{\sin \beta }$$$$=\frac{8}{3}\Rightarrow$$$$\frac{1}{\frac{1}{2}\sin 2\beta }=\frac{8}{3}\Rightarrow$$ $$\frac{2}{\sin 2\beta }=\frac{8}{3}\Rightarrow$$ $$\sin 2\beta =\frac{3}{4}$$
3) Из $$\Delta ACD$$: $$\frac{AC}{\sin 2\beta }=4\sqrt{10}\Rightarrow$$$$AC=4\sqrt{10}*\frac{3}{4}=3\sqrt{10}$$; $$\sin \varphi =\frac{2*\frac{93}{2}}{\frac{16\sqrt{2}}{\sqrt{5}} * 3\sqrt{10}}=$$$$\frac{93}{16*3*2}=\frac{93}{96}\Rightarrow$$ $$\angle \varphi=\arcsin \frac{31}{32}$$
Задание 16
Фирма планирует взять в январе кредит на целое число миллионов рублей на четыре года на следующих условиях:
Найдите наименьший размер кредита, при котором общая сумма выплат фирмой превысит 100 млн. рублей.
Пусть взяли S млн.руб ($$S \in N$$), A-сумма выплат во 2-ой и 4-ой год . Т.к. в 1-ой и 2-ой год выплачивались только проценты, то можно рассмотреть ситуацию кредита на 2 года с платежом А , процентом 10%. Составим таблицу изменения долга и платежей:
| Год | Долг | Долг с процентом | Платеж |
| 1 | S | S+0,1S | 0,1S |
| 2 | S | S+0,1S | A |
| 3 | 1,1S-A | 1,1S-A+0,1(1,1S-A) | 0,1(1,1S-A) |
| 4 | 1,1S-A | 1,1S-A+0,1(1,1S-A) | A |
Рассмотрим 4ый год: $$(\frac{11}{10})^{2}S-A(1,1+1)=0\Leftrightarrow$$ $$A=\frac{11^{2}S}{10^{2}*2,1}=\frac{121S}{21*10}=\frac{121S}{210}$$
Тогда процент после 1-го : S*0,1
После третьего : $$(S+0,1S-\frac{121S}{210})*0,1=\frac{11S}{210}$$
Итоговые выплаты: $$\frac{S}{10}+\frac{11S}{210}+2*\frac{121 S}{210}>100\Leftrightarrow$$$$\frac{S}{10}+\frac{11S}{210}+\frac{242S}{210}>100\Leftrightarrow$$$$\frac{274S}{210}>100\Leftrightarrow$$$$S>76,6\Rightarrow S=77$$
Задание 17
Найдите все значения параметра a , при которых система уравнений $$\left\{\begin{matrix}3(\sqrt{x|x|}+|y|-3)(|x|+3|y|-9)=0\\ (x-a)^{2}+y^{2}=25\end{matrix}\right.$$ имеет ровно три решения.
$$\left\{\begin{matrix}(3\sqrt{x\left | x \right |}+\left | y \right |-3)(\left | x \right |+3\left | y \right |-9)=0(1)\\(x-a)^{2}+y^{2}=25(2)\end{matrix}\right.$$
Рассмотрим (1) . Это совокупность графиков : $$3\sqrt{x\left | x \right |}+\left | y \right |-3=0$$ и $$\left | x \right |+3\left | y \right |-9=0$$
Т.к $$x\left | x \right |\geq 0$$, то $$x\geq 0$$, следовательно , получим $$3x+\left | y \right |-3=0$$ и $$x+3\left | y \right |-9=0$$ или $$\left\{\begin{matrix}\left[\begin{matrix}x=\frac{3-\left | y \right |}{3}\\x=9-3\left | y \right |\end{matrix}\right.(1)\\x\geq 0\end{matrix}\right.$$
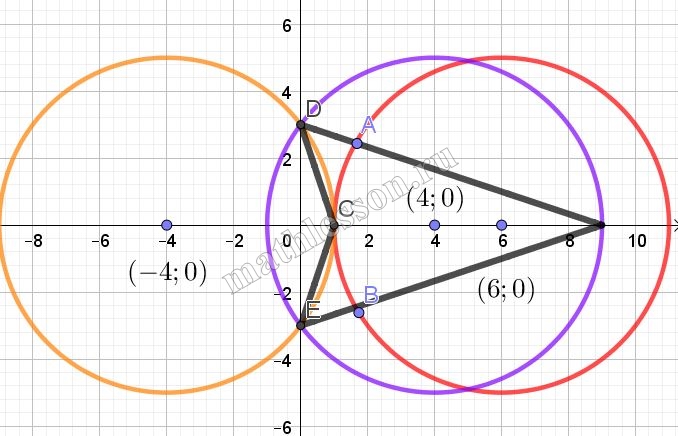
(2): окружность радиуса 5 и центром (a;0). Построим график (1)
Тогда есть 3 случая, чтобы было 3 решения.
1) Проходит через С (1;1) и центр правее этой точки (А;B)$$\Rightarrow a=6$$ (красная окружность)
2) Проходит через (1;1) и центр левее (D,C,E- точки пересечения)$$\Rightarrow a=-4$$ (оранжевая)
3) Проходит через(0;3) ;(0;-3);(9;0) $$\Rightarrow a=4$$ (синяя)
Задание 18
Конечная последовательность a1,a2,...,an состоит из $$n \geq 3$$ не обязательно различных натуральных чисел, причем при всех натуральных $$k \leq n-2$$ выполнено равенство $$a_{k+2}=2a_{k+1}-a_{k}+1$$.
$$a_{1}, a_{2} .., a_{n }, n \geq 3$$. При $$\forall k \leq n-2$$; $$a_{n+2}=2a_{k+1}-a_{k}+1$$
A) Видим, что $$a_{k+2}-a_{k+1}=a_{k+1}-a_{k}+1$$. Т.е разница соседних членов увеличивается на 1. Если $$a_{5}=3$$, то пусть $$a_{4}=3$$. Разница $$a_{5}-a_{4}=0$$, следовательно , $$a_{4}-a_{3}=-1$$, $$a_{3}-a_{2}=-2$$, $$a_{2}-a_{1}=-3$$. Получим : 9 6 4 3 3.
Б) Последовательность с какого-то момента возрастает .При этом , чтобы $$a_{3}=a_{11}$$ она должна сначала возрастать . Тогда будет 2 одинаковых члена (когда их разность равна 0) , но 11-2=9 , то есть с $$a_{3}$$ по $$a_{11}$$ - 9 членов , с учетом необходимости симметрии нужно четное количество , следовательно, не может.
В) Очевидно, что наибольшее количество чисел, в случае, когда есть убывание и возрастание . Рассмотрим симметрию в середине числа 50:
4 10 15 19 22 24 25 25 26 28 31 35 40 46
Мы видим, что можем сдвинуть центр на 3 единицы влево (до 1) :
1 7 12 16 19 21 22 22 23 25 28 32 37 43 50
Всего 15 чисел.