315 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
Задание 2
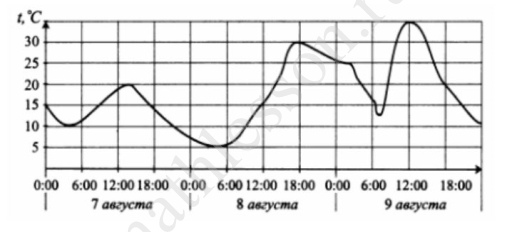
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 8‐го августа. Ответ дайте в градусах Цельсия.
Задание 10
Груз массой 0,4 кг колеблется на пружине. Его скорость $$v$$ меняется по закону $$v=v_{0}\cos \frac{2\pi t}{T}$$, где t — время с момента начала колебаний, T=2 с — период колебаний, $$v_{0}=0,6$$м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле $$E=\frac{mv^{2}}{2}$$, где m — масса груза в килограммах, $$v$$ — скорость груза в м/с. Найдите кинетическую энергию груза через 36 секунд после начала колебаний. Ответ дайте в джоулях.
Задание 14
В основании треугольной призмы АВСА1В1С1 лежит прямоугольный треугольник АВС с прямым углом В. На ребре ВС взята точка L, причем BL:LC=1:2
Задание 16
В треугольнике АВС точка О – центр описанной окружности. Прямая BD, перпендикулярная прямой АО, пересекает сторону АС в точке D, а описанную вокруг треугольника АВС окружность – в точке Т.
Задание 17
15 декабря планируется взять кредит в банке на 2400 тыс. рублей на (n+2) месяца. Условии его возврата таковы:
Найдите n, если всего было выплачено банку 3690 тыс. рублей.
Задание 19
Набор состоит из сорока пяти целых положительных чисел, среди которых есть числа 6, 7, 8. Среднее арифметическое любых тридцати пяти чисел этого набора меньше 2.