319 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.

Одна таблетка лекарства весит 40 мг и содержит 6$$\%$$ активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,2 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в возрасте четырёх месяцев и весом 6 кг в течение суток?

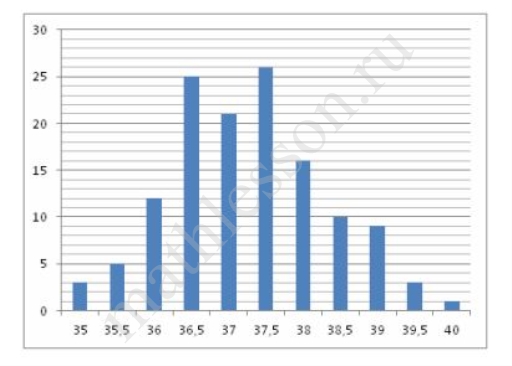
На гистограмме показано распределение больных больницы по температуре. По горизонтали указывается температура, по вертикали - количество больных с данной температурой. Определите по гистограмме, сколько больных имеют нормальную температуру (от 36 до 37 градусов).

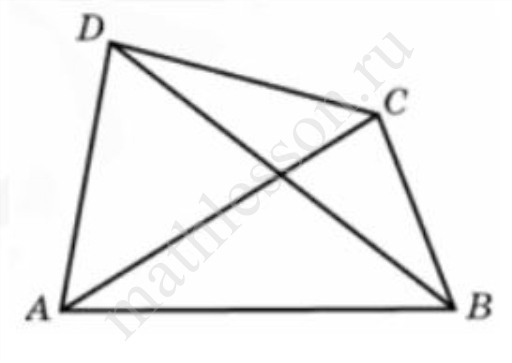
Найдите угол ADB (в градусах), изображенный на рисунке.

Угол DAB равен $$30{}^\circ $$, угол АСВ равен $$80{}^\circ $$. DB - касательная к окружности.

На рисунке изображен лабиринт. Жук вползает в лабиринт в точке «Вход». Развернуться и ползти назад жук не может, поэтому на каждом разветвлении жук выбирает один из путей, по которым он еще не полз. Считая, что выбор число случайный, определите, с какой вероятностью жук придет к одному из выходов. Ответ округлите до сотых.

Найдите произведение всех различных корней уравнения $$x^2-4x+1=4\sqrt{x^2-4x-2}$$

Диагонали четырехугольника равны 7 и 10. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

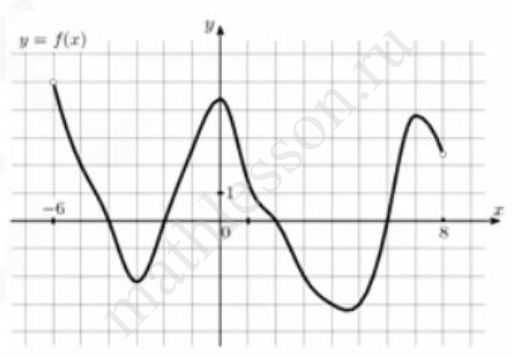
На рисунке изображен график функции $$y=f(x)$$, определенной на интервале $$(-6;8)$$. Определите количество целых точек, в которых производная функции положительна.

Объем параллелепипеда $$ABCDA_1B_1C_1D_1$$ равен 9. Найдите объем треугольной пирамиды $$ABDA_1$$.

Найдите значения выражения $$14\sqrt{6}{\cos \frac{19\pi }{6}\cdot{\cos \frac{7\pi }{4}\ }\ }$$

Плоский замкнутый контур площадью $$S=0,625$$ м$${}^{2}$$ находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой $${\varepsilon }_i=aS{\cos \alpha \ }$$, где $$\alpha $$ - острый угол между направлением магнитного поля и перпендикуляром к контуру, $$a=16*{10}^{-4}$$ Тл/с ? постоянная, $$S$$ - площадь замкнутого контура, находящегося в магнитном поле (в м$${}^{2}$$). При каком минимальном угле $$\alpha $$ (в градусах) ЭДС индукции не будет превышать $$5*{10}^{-4}$$ В?

Теплоход прошёл путь от пункта А до пункта В за 6 часов. В некоторый момент плавания с борта теплохода на воду была спущена моторная шлюпка, которая вернулась в пункт А и без задержки направилась в пункт В, прибыв туда одновременно с теплоходом. Теплоход и шлюпка двигались равномерно и без остановок, причём скорость шлюпки вдвое превышала скорость теплохода. Определите, через какое время после отплытия теплохода из пункта А на воду была спущена шлюпка? Ответ дайте в часах.

Найдите точку минимума функции $$y=\left(73-x\right)*e^{73-x}$$

а) Решите уравнение $$\left|{\cos x\ }+{\cos 3x\ }\right|=-{\cos 2x\ }$$

б) Укажите корни этого уравнения, принадлежащие отрезку $$\left[-\pi ;\frac{\pi }{2}\right]$$

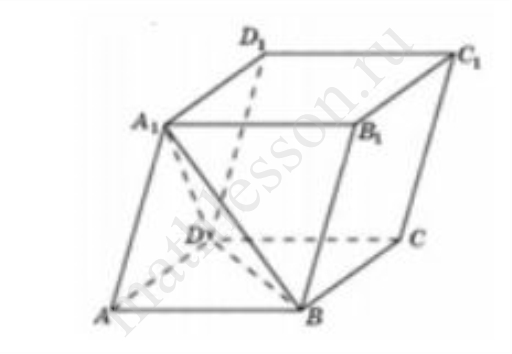
Дана правильная призма $$ABCA_1B_1C_1$$, у которой сторона основания $$AB=4$$, а боковое ребро $$AA_1=9$$, Точка М - середина ребра АС, а на ребре $$AA_1$$ взята точка Т так, что $$AT=3$$.

а) Докажите, что плоскость $$BB_1M$$ делит отрезок $$C_1T$$ пополам.

б) Плоскость $$BTC_1$$ делит отрезок $$MB_1$$ на две части. Найти длину большей из них. 

Решите неравенство $$x{{\log }_8 (\frac{x}{5}-1)\ }\ge 3{{\log }_2 (\frac{x}{5}-1)\ }$$

Биссектрисы углов С и D четырехугольника ABCD пересекаются в точке К. Диагональ BD разбивает отрезок КС в отношении 2:1, считая от вершины С. При этом площадь треугольника ACD в два раза больше площади треугольника AKD.

а) Докажите, что угол CKD прямой

б) Найдите ВК, если ВС=6

15 декабря планируется взять кредит в банке на $$S$$ тысяч рублей на 52 месяца. Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

- со 2-го по 14 число каждого месяца необходимо выплатить часть долга;

- 15-го числа первый и второй месяцы долг должен уменьшиться на 600 тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на $$a$$ тысяч рублей.

Найдите все значения параметра $$a$$, при каждом из которых уравнение

$$a\sqrt{1-\frac{1}{x^2}}+\left|1-\frac{\left|x\right|}{2}\right|=1$$

имеет ровно два различных корня.

На окружности некоторым образом расставили натуральные числа от 4 до 30 (каждое число поставлено по одному разу). Затем для каждой пары соседних чисел нашли разность большего и меньшего.

а) Могли ли все полученные разности быть не меньше 14?

б) Могли ли все полученные разности быть не меньше 13?

в) Помимо полученных разностей, для каждой пары чисел, стоящих через одно, нашли разность большего и меньшего. Для какого наибольшего целого числа $$k$$ можно так расставить числа, чтобы все разности были не меньше $$k$$?