409 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
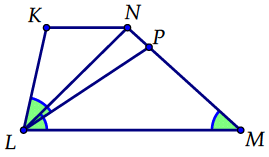
Задание 1
$$\Delta LKN\sim\Delta LPM$$
$$\frac{LK}{LP}=\frac{LN}{LM}=\frac{4x}{6x}$$
$$LK=\frac{2}{3}\cdot18=12$$
Задание 2
$$S_{пов. шара}=4\pi\cdot R^2=4\pi\cdot0,9^2$$
Внутри куба лежит $$\frac{1}{4}$$ чаcть шара.
$$\frac{1}{4}\cdot4\pi\cdot0,9^2=0,9^2\pi$$
$$0,9^2=0,81$$
Задание 3
$$P=0,9\cdot0,1+0,1\cdot0,9=0,18$$
Задание 4
Вероятность поразить цель с первого выстрела равна $$0,9$$.
Но есть вероятность и того что цель будет поражена со второго выстрела и она равна: $$0,1\cdot0,9=0,09$$.
Вероятность того, что цель не будет поражена и со второго выстрела равна:
$$0,1\cdot0,1=0,01$$
Значит, тогда вероятность того, что цель будет поражена с третьего выстрела равна: $$0,01\cdot0,9=0,009$$
Задание 5
$$(2+\log_5x)^2-6\log_5x=24$$
$$t=\log_5x$$
$$4+4t+t^2-6t=24$$
$$t^2-2t-20=0$$
$$t=1\pm\sqrt{21}$$
$$\log_5x=1\pm\sqrt{21}$$
$$x=5^{1\pm\sqrt{21}}$$
$$5^{1+\sqrt{21}}\cdot5^{1-\sqrt{21}}=25$$
Задание 6
$$\sqrt{3}\cdot\frac{\sin75^{\circ}\cos15^{\circ}-\sin165^{\circ}\sin15^{\circ}}{\sin35^{\circ}\sin205^{\circ}+\sin305^{\circ}\cos205^{\circ}}=\sqrt{3}\cdot\frac{\sin75^{\circ}\cos15^{\circ}-\cos75^{\circ}\sin15^{\circ}}{\sin35^{\circ}\sin25^{\circ}+\cos35^{\circ}\cos25^{\circ}}=$$
$$=\sqrt{3}\cdot\frac{\sin(75^{\circ}-15^{\circ})}{\cos(35^{\circ}+25^{\circ})}=3$$
Задание 8
$$2\sin(\frac{2\pi}{3}t+\frac{\pi}{12})\geq1$$
$$\frac{\pi}{6}+2\pi k\leq\frac{2\pi}{3}t+\frac{\pi}{12}\leq\frac{5\pi}{6}+2\pi k,k\in Z$$
$$\frac{\pi}{12}+2\pi k\leq\frac{2\pi}{3}t\leq\frac{3\pi}{4}+2\pi k$$
$$\frac{1}{8}+3k\leq t\leq\frac{9}{8}+3k$$
$$k=0$$
$$\frac{7}{8}\cdot100=\frac{175}{2}=87,5$$
Задание 9
В первом случае монтёр спускался со скоростью, равной собственной скорости и скорости эскалатора, а именно, со скоростью $$\frac{1}{24}$$ ед/с, а во втором случае - только с собственной скоростью, равной $$\frac{1}{42}$$ ед/с, следовательно, скорость эскалатора равна:
$$\frac{1}{24}-\frac{1}{42}=\frac{1}{56}$$ ед/с,
откуда получается, что чистое время спуска по эскалатору равно:
$$\frac{1}{\frac{1}{56}}=56$$ с
Задание 10
Горизонтальная асимптота: $$x=4; y=-2$$
$$f(x)=\frac{k}{x-4}-2$$
Точка $$(1;-1)$$ принадлежит графику функции. Тогда:
$$-1=\frac{k}{-3}-2$$
$$1=\frac{k}{-3}$$
$$k=-3$$
$$f(x)=\frac{-3}{x-4}-2$$
$$f(29)=-\frac{3}{25}-2=-2,12$$
Задание 11
$$y'=-8+\frac{4}{4x}=\frac{1}{x}-8=\frac{1-8x}{x}$$
$$x=\frac{1}{8}$$ - точка максимума
$$y(\frac{1}{8})=16-1+\ln\frac{1}{2}+\ln2=15$$