389 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.

$$5\cdot\sqrt[4]{16^{3x-7}}-2\cdot\sqrt{4^{3x-7}}=12$$

$$5\cdot(2^{4(3x-7)})^{\frac{1}{4}}-2\cdot(2^{2(3x-7)})^{\frac{1}{2}}=12.$$

$$5\cdot2^{3x-7}-2\cdot2^{3x-7}=12$$

$$3\cdot2^{3x-7}=12$$

$$2^{3x-7}=4$$

$$3x-7=2$$

$$3x=9$$

$$x=3$$

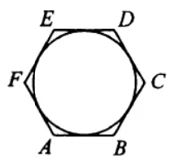
Рассмотрим равносторонний треугольник AOB (известно, что правильный шестиугольник разбивается на шесть правильных треугольников) с высотой, равной радиусу вписанной окружности r (см. рисунок ниже).

​​

Так как все углы правильного треугольника равны 60°, то радиус r равен:

$$r=AO\cdot\sin60^{\circ}=\sqrt{3}\cdot\frac{\sqrt{3}}{2}=1,5$$.

$$\frac{52\sin(\frac{6001\pi}{6})}{\sin(-\frac{15\pi}{4})\cdot\cos(-\frac{15\pi}{4})}=\frac{52\sin(100\pi+\frac{\pi}{6})}{\sin\frac{\pi}{4}\cos\frac{\pi}{4}}=$$

$$=\frac{52\sin(\frac{\pi}{6})}{\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{2}}{2}}=\frac{52\cdot\frac{1}{2}}{\frac{1}{2}}=52$$

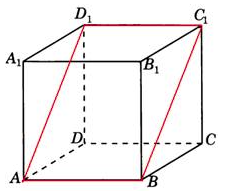
Так как параллелепипед $$ABCDA_1B_1C_1D_1$$ прямоугольный, то все углы сечения $$ABC_1D_1$$ будут прямыми. Кроме того, противоположные стороны сечения также равны, то есть $$AD_1=BC_1$$ и $$AB=D_1C_1.$$ Следовательно, сечение представляет собой прямоугольник.

Найдем площадь сечения как произведение двух его сторон $$S=AB\cdot BC_1.$$ Сторона $$AB=4,$$ сторону $$BC_1$$ найдем из прямоугольного треугольника $$BCC_1$$ по теореме Пифагора:

$$BC_1=\sqrt{36+64}=\sqrt{100}=10$$

и

$$S=4\cdot10=40$$

$$ax^2+34=8x+2$$

$$ax^2-8x+32=0$$

$$D=64-128a=0$$

$$128a=64$$

$$a=\frac{64}{128}=0,5$$

50% от $$I_{кз}:$$

$$\frac{50}{100}\cdot\frac{\varepsilon}{r}=\frac{1}{2}\cdot\frac{\varepsilon}{r}=\frac{\varepsilon}{2r}=\frac{\varepsilon}{2\cdot2}=\frac{\varepsilon}{4}$$

Наименьшее сопротивление:

$$\frac{\varepsilon}{4}\geq\frac{\varepsilon}{R+r}$$ $$|\cdot\frac{4}{\varepsilon}$$

$$1\geq\frac{4}{R+2}$$ $$|\cdot(R+2)$$

$$R+2\geq4$$

$$R\geq2$$

Пусть x рабочих, работая y часов выполняют всю работу за 14 дней. Тогда 14xy – вся работа.

$$(x+4)$$ рабочих, работая $$(y+1)$$ час выполняют работу за 10 дней.

$$(x+4)\cdot(y+1)$$– часть работы за один день

$$(x+4)\cdot(y+1)=\frac{14xy}{10}$$

$$(x+10)$$ рабочих, работая $$(y+2)$$ час выполняют работу за 7 дней.

$$(x+10)\cdot(y+2)$$– часть работы за один день

$$(x+10)\cdot(y+2)=\frac{14xy}{7}$$

Система двух уравнений с двумя неизвестными:

$$\left\{\begin{matrix} (x+4)(y+1)=\frac{14xy}{10}\\ (x+10)(y+2)=\frac{14xy}{7} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 10xy+40y+10x+40=14xy\\ xy+10y+2x+20=2xy \end{matrix}\right.\Leftrightarrow$$

$$\Leftrightarrow\left\{\begin{matrix} 20y+5x+20=2xy\\ 10y+2x+20=2xy \end{matrix}\right.$$

Умножаем второе на $$(–2)$$ и складываем

$$x=20$$ рабочих

Точка $$(0;-1)$$ принадлежит графику функции. Тогда:

$$f(0)=b=-1$$

$$b=-1$$

Пусть 10000 - количество изделий. Из них 5%, т.е. 500 - брак, а 95% - небракованные изделия.

Так как нам подходит всего 75% небракованных изделий, а это $$0,75\cdot(10000-500)=7125,$$ то вероятность выбрать первосортное изделие:

$$P(A)=\frac{7125}{10000}=0,7125$$

$$y'=1-\frac{32}{x^5}=\frac{x^5-32}{x^5}=\frac{(x-2)(x^4+2x^3+4x^2+8x+16)}{x^5}$$

$$f(-1)=-1+\frac{8}{(-1)^4}=7$$

$$f(-2)=-2+\frac{8}{(-2)^4}=-1,5$$ - ответ