322 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Задание 1
Стрекоза и муха двигаются по прямой. Стрекоза догоняет муху, их скорости равны 1,2 м/с и 30 см/с. Через сколько секунд расстояние между насекомыми сократится с 6,5 м до 20 см?
Задание 2
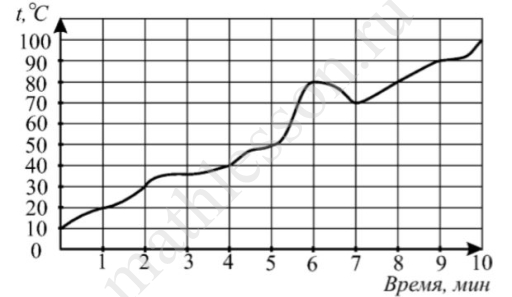
На графике (см. рис.) показан процесс нагревания некоторого прибора. На оси абсцисс откладывается время в минутах, прошедшее с момента включения прибора, на оси ординат температура прибора в градусах Цельсия.
Определит по рисунку, за сколько секунд прибор нагреется от $$30{}^\circ C$$ до $$80{}^\circ C$$
Задание 3
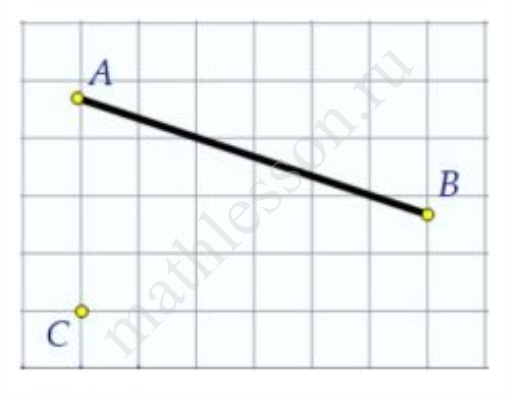
На клетчатой бумаге с размером клетки 1 см $$\times$$ 1 см отмечены прямая АВ и точка С. Найдите расстояние в см от точки С до прямой АВ. В ответе записать найденное расстояние, умноженное на $$\sqrt{10}$$.
Построим треугольник CKM по целым клеткам. Найдем его площадь, вычитая из площади прямоугольника (внутри которого можно поместить данный треугольник) площади прямоугольных треугольников (площади отмечены на рисунке, как половина произведения катетов). То есть: $$3\cdot 5-\frac{1}{2}\cdot 2\cdot 3-\frac{1}{2}\cdot 3\cdot 1-\frac{1}{2}\cdot 2\cdot 5=5,5$$
Учтем, что его площадь можно так же найти как половину произведения KM на высоту h(расстояние от C до KM). При этом KM найдем по теореме Пифагора $$KM=\sqrt{3^{2}+1^{2}}=\sqrt{10}$$. Тогда $$h=\frac{2\cdot 5,5}{\sqrt{10}}=\frac{11}{\sqrt{10}}$$. В ответ укажем число, умноженное на $$\sqrt{10}$$, то есть 11
Задание 4
На отрезке $$\left[-7;18\right]$$ числовой оси случайным образом отмечают одну точку. Найти вероятность того, что координата отмеченной точки будет больше $$-5$$, но меньше 9.
Задание 5
Решите уравнение $$\left|x^2-8x+5\right|=2x$$. Если уравнение имеет более одного корня, в ответе укажите больший рациональный корень.
Задание 6
В треугольнике MNP известно, что $$MM_1$$ и $$PP_1$$ - медианы, $$MM_1=9\sqrt{3},PP_1=6,\angle MOP=150{}^\circ .$$ Найдите радиус окружности, описанной около треугольника $$MOP$$.
Задание 7
При движении тела по прямой расстояние S (в метрах) до точки отсчета изменялось по закону: $$S\left(t\right)=5t^2-t^3+9t$$, где t - время в секундах, прошедшее от начала движения. Через сколько секунд после начала движения ускорение тела было равно 1 м/с$${}^{2}$$?
$$S'\left(t\right)=V\left(t\right);$$
$$V'\left(t\right)=a\left(t\right)\to$$ $$S''\left(t\right)=a(t)$$
Тогда $$10-6t=1\to 6t=9\to t=1,5$$
Задание 8
В прямоугольном параллелепипеде $$ABCDA_1B_1C_1D_1$$ известны отношения длин ребер: $$AB:AD:{AA}_1=16:15:34$$. Расстояние от центра грани $$ABB_1A_1$$ до вершины D равно $$34\sqrt{2}.$$ Найдите сумму длин всех ребер параллелепипеда.
$$BD_1=HM$$, где $$BH\bot AB$$, $$M$$ - середина $$DD_1$$
Пусть $$AB=16x\to AH=8x$$ $$MD=17x\to HD=\sqrt{{\left(8x\right)}^2+{\left(15x\right)}^2}=17x;$$
$$HM=\sqrt{{\left(17x\right)}^2+{\left(17x\right)}^2}=34\sqrt{2}\to$$ $$\sqrt{578x^2}=\sqrt{1156\cdot 2}\to x=2 \to$$ $$\to AB=32;AD=30;AA_1=68.$$
Сумма длин: $$\left(32+30+68\right)\cdot 4=520$$
Задание 9
Найдите значение выражения $$\frac{{{\sin }^3 \alpha \ }-{{\cos }^{{\rm 3}} \alpha \ }}{{\sin \alpha \ }-{\cos \alpha \ }}-\frac{{\cos \alpha \ }}{\sqrt{1+{{\ctg }^{{\rm 2}} \alpha \ }}}-2{\tg \alpha \ }{\ctg \alpha \ }$$, если известно, что $$\frac{\pi }{2}<\alpha <\pi $$
Задание 10
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону $$U=U_0{\sin (\omega t+\varphi )\ }$$, где t - время (в секундах), амплитуда напряжения $$U_0=2$$ В, частота $$\omega =\frac{2\pi }{3}$$, фаза $$\varphi =\frac{\pi }{12}$$. Датчик настроен так, что если напряжение U в нем не ниже чем 1 В, загорается лампочка. Какую часть времени, в процентах, на протяжении первой секунды после начала работы лампочка будет гореть?
Учтем, что рассматривается первая секунда $$\to \frac{2}{3}t+\frac{1}{12}=\frac{1}{6}\to \frac{2}{3}t=\frac{1}{12}\to t=\frac{1}{8}$$.
То есть с момента 0,125 с будет гореть лампочка $$\to 87,5\%$$
Задание 11
На вагоноремонтном заводе в определенный срок должно быть отремонтировано 330 вагонов. Перевыполняя план ремонта в среднем на 3 вагона в неделю, на заводе уже за две недели до срока отремонтировали 297 вагонов. Сколько вагонов в неделю ремонтировали на заводе?
Пусть срок $$x$$ недель, в неделю по $$y$$ вагонов
$$ \left\{ \begin{array}{c} xy=330 \\ \left(y+3\right)\left(x-2\right)=297 \end{array} \right.\to$$
$$\left\{ \begin{array}{c} xy=330 \\ xy-2y+3x-6=297 \end{array} \right.$$
Вычтем из первого второе: $$2y-3x=27\to y=\frac{27+3x}{2}$$.
Подставим в первое: $$\left(27+3x\right)x=660\to$$ $$3x^2+27x-660=0\to $$ $$x^2+9x-220=0\to$$ $$\left\{ \begin{array}{c} x_1+x_2=-9 \\ x_1x_2=-220 \end{array} \right. \to$$ $$\left[ \begin{array}{c} x_1=-20 \\ x_2=11 \end{array} \right.\to $$ $$y=\frac{27+33}{2}=30$$ вагонов - было, а 33 ремонтировали.
Задание 12
$$f\left(x\right)=\frac{5^{{{\log }_5 \left(2-x\right)\ }}}{5^{{{\log }_5 \left(x+4\right)\ }}}+6x\to g\left(x\right)=\frac{2-x}{x+4}+6x$$ при $$x\in \left(-4;2\right)\ (M(x))$$
$$\to {\left(x+4\right)}^2=1\to \left[ \begin{array}{c} x=-5\ \\ x=-3 \end{array} \right.$$, где $$x=-5$$ не принадлежит $$M\left(x\right)\to x=-3-min$$
Задание 13
а) Решите уравнение $${\cos 2x\ }-{{\sin }^{{\rm 3}} x\ }\cdot {\cos x\ }+1={{\sin }^{{\rm 2}} x\ }+{\sin x\ }\cdot {{\cos }^{{\rm 3}} x\ }$$
б) Укажите корни этого уравнения, принадлежащие промежутку $$\left(-arctg2;\pi \right)$$
Задание 16
В прямоугольном треугольнике АВС с прямым углом С вписана окружность с центром О, касающаяся его сторон ВС, АС и АВ в точках Р, Q, R соответственно.
Известны длины катетов: $$AC=4$$, $$BC=3$$.
Задание 17
Банк предоставляет кредит сроком на 10 лет под 19% годовых на следующих условиях: ежегодно заемщик возвращает банку 19% от непогашенной части кредита и 1/10 суммы кредита. Так, в первый год, заемщик выплачивает 1/10 суммы кредита и 19% от всей суммы кредита, во второй год заемщик выплачивает 1/10 суммы кредита и 19% от 9/10 суммы кредита и т.д. Во сколько раз сумма, которую выплатит банку заемщик, будет больше суммы кредита, если заемщик не воспользуется досрочным погашением кредита?
Задание 19
На доске написано 35 различных натуральных чисел, каждое из которых либо четное, либо его десятичная запись оканчивается на цифру 7. Сумма всех записанных на доске чисел равна 1135.