259 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 259 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №259 (alexlarin.com)
Решаем ЕГЭ 259 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №259 (alexlarin.com)
Задание 1
Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пакетиков нужно купить хозяйке для приготовления 8 литров маринада?
$$12*8=96$$ г. на 8 литров маринада $$\frac{96}{10}$$$$\Rightarrow$$ 10 пакетиков
Задание 2
На графике точками отмечена максимальная цена (в рублях) одной акции угледобывающей компании в течение каждого из 12 месяцев 2014‐го года. Для наглядности точки соединены отрезками. Определите, сколько месяцев в 2014‐м году максимальная цена одной акции этой компании не превышала 70 руб.
Как видим, таких месяцев 9 штук (все, кроме 2,3 и 11)
Задание 3
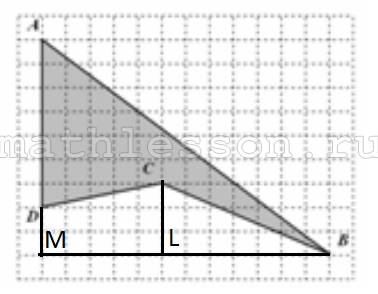
На рисунке клетка имеет размер 1 см х 1 см. Найдите площадь четырехугольника АВСD. Ответ дайте в квадратных сантиметрах.

$$S_{AMB}=\frac{1}{2} AM*MB=\frac{1}{2}*9*12=54$$
$$S_{DMLC}=\frac{DM+CL}{2}*ML=\frac{2+3}{2}*5=12,5$$
$$S_{CLB}=\frac{1}{2} CL*LB=\frac{1}{2}*3*7=10,5$$
$$S_{ABCD}=54-12,5-10,5=31$$
Задание 4
Вероятность того, что новый DVD‐проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD‐ проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Частота события: $$\frac{51}{1000}=0,051$$ Разница: $$0,051-0,045=0,006$$
Задание 5
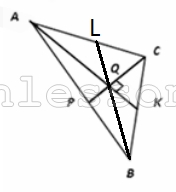
В треугольнике АВС медианы АК и СР пересекаются под прямым углом в точке Q. Найдите длину медианы, проведенной из вершины В треугольника АВС, если известно, что АК=12, СР=9.
1) $$AQ=\frac{2}{3} AK=8$$; $$CQ=\frac{2}{3} CP=6$$(по свойству медиан)
2) из $$\Delta ACQ$$: $$AC=\sqrt{AQ^{2}+QC^{2}}=10$$
3) Пусть BL - медиана $$\Rightarrow$$ $$QL=\frac{1}{2} AC=5$$(свойство медианы прямоугольного треугольника)
4) $$BL=3QL=15$$
Задание 6
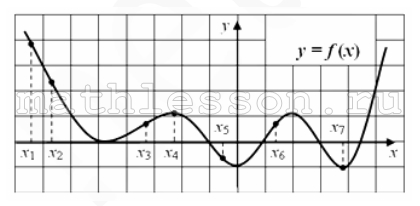
На графике дифференцируемой функции у=f (x) отмечены семь точек: х1,…, х7. Найдите все отмеченные точки, в которых производная функции f(x) равна нулю. В ответе укажите количество этих точек.
$$f'=0$$ в точках экстремума; в данном случае $$x_{4}$$ и $$x_{7}$$ - 2 точки.
Задание 7
В правильной треугольной пирамиде сторона основания равна 3, а двугранный угол при стороне основания равен 30о. Найдите площадь боковой поверхности пирамиды.

1) из $$\Delta ABC$$: $$BM=BC * \sin C=3*\frac{\sqrt{3}}{2}=$$$$\frac{3\sqrt{3}}{2}$$$$\Rightarrow$$ $$MH=\frac{1}{3}$$; $$BM=\frac{\sqrt{3}}{2}$$
2) из $$\Delta DMH$$: $$DM=\frac{MH}{\cos DMH}=$$$$\frac{\sqrt{3}}{2}:\frac{\sqrt{3}}{2}=1$$
3) $$S_{ADC}=\frac{1}{2} DM*AC=$$$$\frac{1}{2} *3*1=1,5$$$$\Rightarrow$$ $$S=3*S_{ADC}=4,5$$
Задание 8
Найдите значение выражения $$\frac{2-4\cos ^{2}19}{5 \sin 128}$$
$$\frac{2-4\cos ^{2}19}{5 \sin 128}=$$$$\frac{2(1-2\cos ^{2}19)}{5 \sin (90+38)}=$$$$\frac{-2\cos 38}{5 \cos 38}=-0,4$$
Задание 9
Мембранный потенциал Em, создаваемый разностью концентраций ионов калия внутри и снаружи мембраны, описывается уравнением Нернста $$E_{m}=E_{0}+\frac{0,059}{h}*lg(\frac{K_{vnesh.}}{K_{vnutr.}})$$. Каким был исходный потенциал E0 (в Вольтах), если мембранный потенциал Em = -0,07В , а внешняя концентрация ионов калия Kвнеш меньше внутренней Kвнут в 10 раз и для калия n = 1.
$$E_{0}=E_{m}-\frac{0,059}{h}*lg(\frac{K_{vnesh.}}{K_{vnutr.}})\Rightarrow$$ $$E_{0}=-0,07-\frac{0,059}{1}*lg \frac{1}{10}=-0,07-0,059*(-1)=-0,011$$
Задание 10
Товарный поезд движется со скоростью 35 км/ч. По соседним путям его обгоняет электричка, идущая со скоростью 95 км/ч. Длина товарного поезда равна 780 м. Найдите длину электрички (в метрах), если известно, что мимо товарного поезда она прошла за 54 секунды.
Пусть x км. - длина электрички , тогда $$t=\frac{S}{v}$$, где S км.- сумма длин поездов ,v км\ч. –разность скоростей, t ч. –время обгона.
$$\frac{54}{3600}=\frac{0,78+x}{95-35}\Leftrightarrow$$ $$\frac{3}{200}=\frac{0,78+x}{60}\Leftrightarrow$$ $$\frac{3}{20}=\frac{0,78+x}{6}\Leftrightarrow$$ $$15,6+20x=18\Leftrightarrow$$ $$20x=2,4\Leftrightarrow$$ $$x=0,12$$ км. $$\Rightarrow$$ 120 метров
Задание 11
Найдите наименьшее значение функции $$y=3x^{4}+4x^{3}-12x^{2}-12$$ на отрезке [-0,5;2].
Найдем производную и приравняем ее к нулю: $${f}'(x)=12 x^{3}+12x^{2}-24x=0\Leftrightarrow$$ $$12x(x^{2}+x-2)=0\Leftrightarrow$$ $$x(x+2)(x-1)=0$$.
На промежутке [-0,5;2] x=1 - точка минимума, следовательно, наименьшее значение функция принимает в этой точке: $$f_{min}=f(1)=3+4-12=-17$$
Задание 12
A) Найдем ОДЗ: $$\left\{\begin{matrix}3 \left | \sin x \right |-\left | \cos x \right |>0\\\left | \cos x \right |>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}3\left | tg x \right |-1>0\\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left | tg x \right |>\frac{1}{3}\\\cos x \neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left[\begin{matrix}tg x>\frac{1}{3}\\tg x<-\frac{1}{3}\end{matrix}\right.\\\cos x \neq 0\end{matrix}\right.$$
Решение: $$\log_{2}(3\left | \sin x\right |-\left | \cos x \right |)+\log_{2}\left | \cos x \right |=0\Leftrightarrow$$$$\log_{2}((3\left | \sin x \right |-\left | \cos x \right |)\left | cos x \right |)=0\Leftrightarrow$$$$3\left | \sin x \cos x \right |-\cos ^{2}x=1\Leftrightarrow$$$$-\cos ^{2}x+3\left | \sin x*\cos x \right |=\sin ^{2}x+\cos ^{2}x\Leftrightarrow$$$$\left | \sin x \right |^{2}-3\left | \sin x \right |\left | \cos x \right |+2 \left | \cos x \right |^{2}=0|:\left | \cos x \right |^{2}\Leftrightarrow$$$$\left | tg x \right |^{2}-3\left | tg x \right |+2=0$$
$$\left[\begin{matrix}\left | tg x \right |=2 \\\left | tg x \right |=1\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}tg x=\pm 2\\tg x= \pm 1\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\pm arctg 2+\pi n \\x=\pm \frac{\pi}{4}+\pi k, n,k \in Z\end{matrix}\right.$$
Б ) Найдем корни на заданном промежутке:
Задание 13
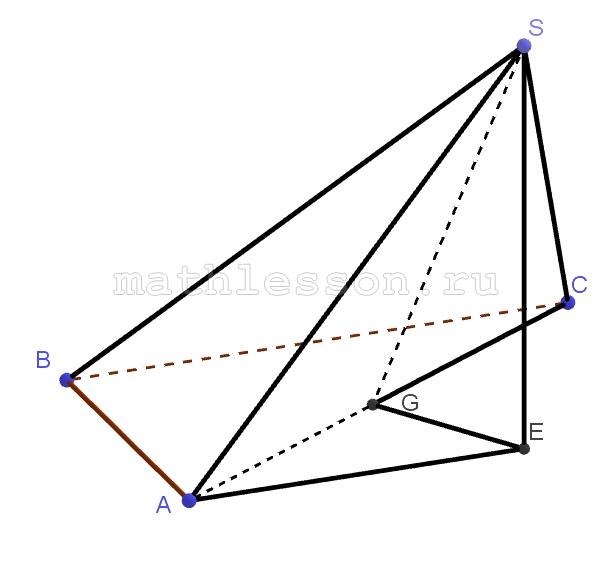
В треугольной пирамиде SABC плоские углы АВС и SAB прямые, двугранный угол между плоскостями ABS и АВС равен $$arcctg(\frac{2\sqrt{10}}{3})$$ . BC=7, AB=4
A) 1) Пусть $$SE \perp (ABC)$$, т.к. $$SA\perp AB$$, то по теореме о трех перпендикулярах : $$AE\perp AB\Rightarrow$$ $$ctg \angle SAE=\frac{2\sqrt{10}}{3}$$. Пусть $$EG\perp AC\Rightarrow$$ $$SG\perp AC$$ (по теореме о 3-x перпендикулярах )$$\Rightarrow$$ $$\angle SGE$$ - искомый
2) $$ctg ^{2}\angle SAE+1=\frac{1}{\sin ^{2}\angle SAE}$$$$\Rightarrow$$ $$\sin \angle SAE=\frac{3}{7}$$. Пусть SE=3x, тогда AS=7x; из $$\Delta ASE$$: $$AE=\sqrt{AS^{2}-SE^{2}}=\sqrt{40}x$$
3) $$\Delta ABC \sim \Delta AGE$$$$\Rightarrow$$ $$\frac{GE}{AB}=\frac{AE}{AC}=\frac{AG}{BC}(1)$$
Из $$\Delta ABC$$: $$AC=\sqrt{AB^{2}+AC^{2}}=\sqrt{65}$$
Из (1): $$AG=\frac{AE*BC}{AC}=\frac{7\sqrt{40}x}{\sqrt{65}}$$; $$GE=\frac{AE*AB}{AC}=\frac{4\sqrt{40}x}{\sqrt{65}}=\frac{8\sqrt{10}x}{\sqrt{65}}$$
4) из $$\Delta ASG$$: $$SG=\sqrt{AS^{2}-AG^{2}}=\frac{35 x}{\sqrt{65}}$$
5) $$\cos \angle SGE=\frac{GE}{SG}=\frac{8\sqrt{10}}{35}$$
Б) Пусть h-высота из B к (ASC) , тогда : $$V_{ABCS}=\frac{1}{3} S_{ASC}*h=\frac{1}{3}*S_{ABC}*SE$$$$\Leftrightarrow$$ $$h=\frac{S_{ABC}*SE}{S_{ASC}}=\frac{\frac{1}{2} *AB*BC*SE}{\frac{1}{2}*SG*AC}=$$$$\frac{AB*BC*SE}{SG*AC}=\frac{4*7*3x}{\frac{35x}{\sqrt{65}}*\sqrt{65}}=\frac{12}{5}$$
Задание 14
Решите неравенство $$\log_{2}(x+1)>\log_{x+1}16$$
ОДЗ: $$\left\{\begin{matrix}x+1>0\\x+1\neq 1\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}x>-1\\x\neq 0\end{matrix}\right.$$$$\Leftrightarrow$$ $$x \in (-1;0)\cup (0; +\infty )$$
Решение: $$\log_{2}(x+1)>4\log_{(x+1)}2$$$$\Leftrightarrow$$ $$\log_{2}(x+1)>\frac{4}{\log_{2}(x+1)}$$
Пусть $$\log_{2}(x+1)=y$$: $$y>\frac{4}{y}\Leftrightarrow$$ $$y-\frac{4}{y}>0$$$$\Leftrightarrow$$ $$\frac{y^{2}-4}{y}>0$$$$\Leftrightarrow$$ $$\frac{(y-2)(y+2)}{y}>0$$$$\Leftrightarrow$$ $$\left[\begin{matrix}y>2\\\left\{\begin{matrix}y>-2\\y<0\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left[\begin{matrix}\log_{2}(x+1)>2\\\left\{\begin{matrix}\log_{2}(x+1)>-2\\\log_{2}(x+1)<0\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left[\begin{matrix}x+1>4\\\left\{\begin{matrix}x+1>\frac{1}{4}\\x+1<1\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$$$\left[\begin{matrix}x>3\\\left\{\begin{matrix}x>-\frac{3}{4}\\x<0\end{matrix}\right.\end{matrix}\right.$$
С учетом ОДЗ: $$x \in (-\frac{3}{4};0)\cup (3;+\infty )$$
Задание 15
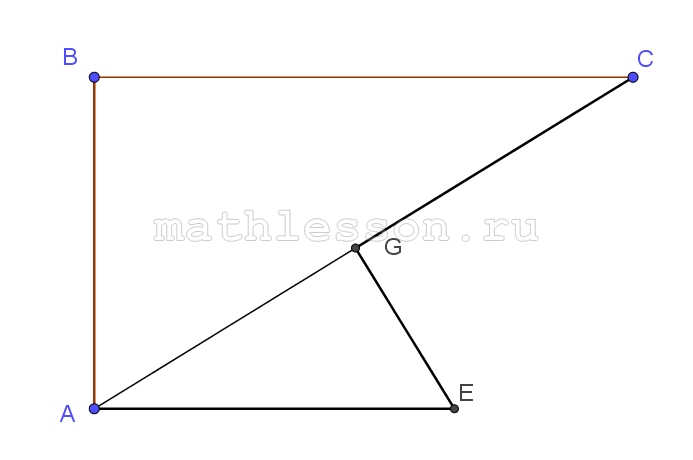
Даны треугольник АВС и ромб BDEF, все вершины которого лежат на сторонах треугольника АВС, а угол при вершине Е – тупой, АЕ=3, СЕ=7, а радиус окружности, вписанной в ромб, равен 1.
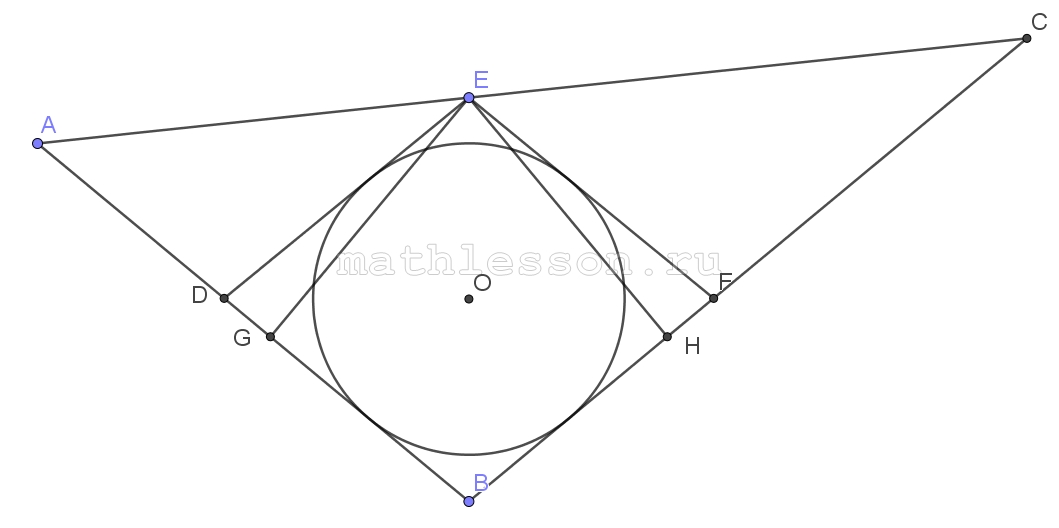
A) 1)Пусть r - радиус вписанной окружности в ромб (r=1); $$EG\perp AB$$; $$EH\perp CB$$. Тогда $$EG=EH=2r=2$$(высота в 2 раза больше радиуса в ромбе) .
2)из $$\Delta AEG$$: $$\sin A=\frac{EG}{AE}=\frac{2}{3}$$$$\Rightarrow$$ $$\cos A=\frac{\sqrt{5}}{3}$$
Из $$\Delta ECH$$: $$\sin C=\frac{EH}{EC}=\frac{2}{7}$$$$\Rightarrow$$ $$\cos C=\frac{\sqrt{45}}{7}=\frac{3\sqrt{5}}{7}$$
Из $$\Delta ACB$$: $$\sin B=\sin (180-(A+C))=\sin (A+C)$$
$$\sin (A+C)=\sin A* \cos C+\sin C*\cos A=$$$$\frac{2}{3}*\frac{3\sqrt{5}}{7}+\frac{2}{7}*\frac{\sqrt{5}}{3}=$$$$\frac{8\sqrt{5}}{21}\Rightarrow$$ $$\cos (A+C)=-\frac{11}{21}$$ ($$\angle A+\angle C>90$$)
3)По т. cинусов : $$\frac{AB}{\sin C}=\frac{AC}{\sin B}\Rightarrow$$ $$AB=10*\frac{2}{7}:\frac{8\sqrt{5}}{21}=\frac{3\sqrt{5}}{2}$$
4) $$S_{ABC}=\frac{1}{2}*AB*AC* \sin A=5\sqrt{5}$$
Б) 1) По т. синусов : $$\frac{AB}{\sin C}=\frac{BC}{\sin A}=\frac{AC}{\sin B}$$$$\Rightarrow$$ $$AB=\frac{AC*\sin C}{\sin B}=\frac{3\sqrt{5}}{2}$$; $$BC=\frac{AC* \sin A}{\sin B}=\frac{7\sqrt{5}}{2}$$. Тогда $$p=\frac{AB+AC+BC}{2}=\frac{10+5\sqrt{5}}{2}$$
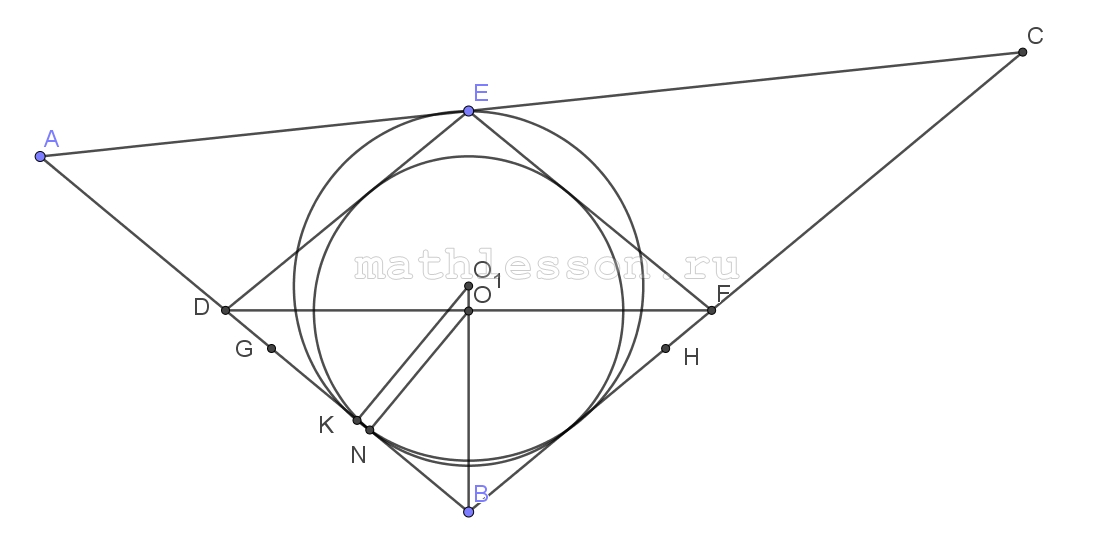
2) Пусть $$R=KO_{1}$$ - радиус вписанной в $$\Delta ABC$$ $$\Rightarrow$$ $$R=\frac{S}{p}=10-4\sqrt{5}$$
3) $$\angle KBO=\frac{\angle B}{2}\Rightarrow$$ $$\cos \angle B=1-2 \sin ^{2}\angle KBO\Rightarrow$$ $$\sin \angle KBO=\frac{4}{\sqrt{21}}$$
4) из $$\Delta KO_{1}B$$: $$BO_{1}=\frac{O_{1}K}{\sin \angle KBO}=\frac{(10-4\sqrt{5})\sqrt{21}}{4}$$
Из $$\Delta NOB$$: $$OB=\frac{ON}{\sin \angle KBO}=\frac{\sqrt{21}}{4}$$
$$OO_{1}=BO_{1}-BO=\frac{\sqrt{21}}{4}(10-4\sqrt{5}-1)=\frac{\sqrt{21}}{4}(9-4\sqrt{5})$$
Задание 16
Тема сделал несколько мелких покупок в супермаркете, имея при себе сто рублей. Давая сдачу с этой суммы, кассир ошиблась, перепутав местами цифры, и выплатила рублями то, что должна была вернуть копейками, и, наоборот, копейками то, что должна была вернуть рублями. Купив в аптеке набор пипеток за 1 руб.40 коп., Тема обнаружил ошибку кассира и, пересчитав деньги, нашел, что оставшаяся у него сумма втрое превышает ту, которую ему должны были вернуть в супермаркете. Какова стоимость всех покупок Темы?
Пусть правильная сдача n рублей и m копеек $$\Rightarrow$$ $$100n+m$$ копеек. Кассир не дала m рублей и n копеек $$\Rightarrow $$100m+n копеек. После покупки пипеток у Темы остается : $$(100m+n-140)$$ копеек. Эта сумма в 3 раза больше, чем $$100n+m$$:
$$3(100n+m)=(100m+n-140)\Leftrightarrow$$$$300n+3m=100m+n-140\Leftrightarrow$$$$299n=97m-140, n,m \in N$$ и $$(n,m \leq 99)\Leftrightarrow$$$$m=\frac{299n+140}{97}=3n+1+\frac{8n+43}{97}$$
Тогда $$\frac{8n+43}{97}\in N$$ или 0 (0 не может быть, так как тогда n отрицательное) $$\Rightarrow$$ $$\frac{8n+43}{97}=k$$$$\Rightarrow$$ $$\frac{97k-43}{8}=n=12k-5+\frac{k-3}{8}$$
Тогда $$\frac{k-3}{8}\in N$$ или 0 (то есть делится нацело на 8: $$\frac{k-3}{8}=0\Rightarrow$$ $$k=3\Rightarrow$$ $$n=12*3-5=31\Rightarrow$$ $$m=\frac{299*31+140}{97}=97$$
Тогда правильная сдача 31 рубль 97 копеек $$\Rightarrow$$ покупка 68 рублей 3 копейки . С учетом 1 рубля 40 копеек получим , что общая покупка 69 рублей 43 копейки.
Задание 17
Найдите все значения параметра a, для которых при любом положительном b уравнение $$a \log_{\frac{1}{x}-2}4=\log_{2}(\frac{1}{x}-2)-b$$ имеет хотя бы одно решение, меньшее $$\frac{1}{3}$$
Так как $$x<\frac{1}{3}$$, то $$\frac{1}{x}-2>1$$. Пусть $$\frac{1}{x}-2=y$$. Тогда получим : $$a \log_{y}4=\log_{2}y-b$$$$\Leftrightarrow$$ $$2a \log_{y}2+b=\log_{2}y$$
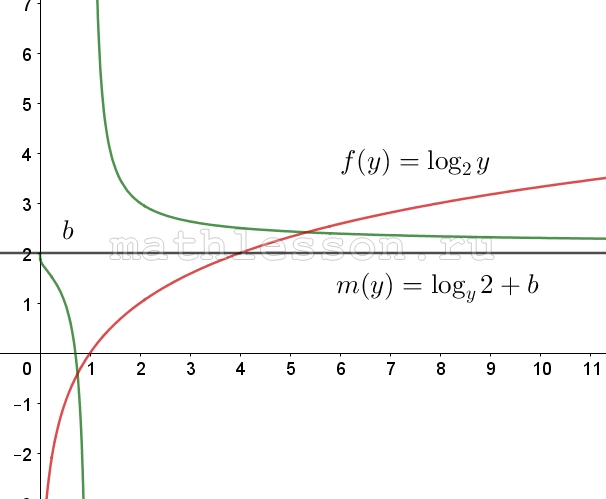
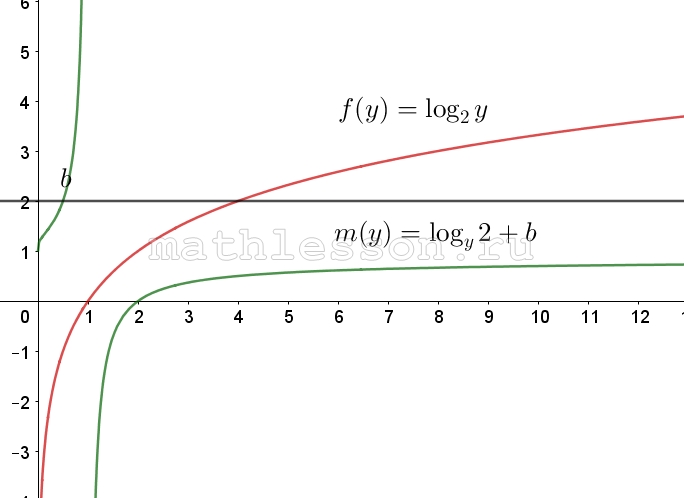
Пусть $$f(y)=2a \log_{y}2+b$$ и $$g(y)=\log_{2}y$$
Рассмотрим $$f(y)$$: данный график имеет растяжение по Oy и располагается так же как $$m(y)=\log_{y}2+b$$ при $$a>0$$. При a<0 симметрично отобразится относительно Ox .
Необходимо решение при y>1. На данном промежутке $$m(y)=\log_{y}2+b$$ убывает, при этом $$\lim _{y\rightarrow \infty }m(y)=b$$ и предел достигается сверху. Следовательно, при a>0 и b>0, $$\lim _{y\rightarrow \infty }f(y)=b\Rightarrow$$ будет пересечение с g(y) , т.к. $$\lim_{y\rightarrow \infty }g(y)=\infty$$
При $$a<0$$ , $$f(y)$$ на $$y>1$$ возрастает и $$\lim _{y\rightarrow \infty } f(y)=b$$. При этом предел достигается снизу, и так как в задании необходимо решение для любого положительного b, а, например, при b=0,1, пересечений графика f(y) и g(y) не будет. Следовательно, данный промежуток мы не учитываем.
При a=0 имеем $$\log_{2}y=b\Rightarrow y=2^{b}$$. Т.к. $$b>0$$, то $$y>1$$ $$\Rightarrow$$ $$a \in [0;+\infty)$$
Задание 18
A) Пусть дано число $$10^{n}a_{n}+10^{n+1}a_{n+1}+10^{1}*a_{1}+a_{0}$$. Если мы вычтем из него сумму цифр, то получим : $$(10^{n}-1)a_{n}+(10^{n-1}-1)a_{n-1}+...+(10^{1}-1)a_{1}$$. Видим, что каждый из множителей $$(10^{n}-1)$$; $$(10^{n-1}-1)$$ и т.д. кратен 9 $$\Rightarrow$$ полученное число кратно 9 . Но 1 не кратно 9 $$\Rightarrow$$ не может .
Б) Раз последнее равно 0 и разность последнего и предпоследнего кратно 9, то очевидно, что предпоследнее 9.
B) Аналогично, Б и учитывая, что каждая разность делится на 9 , получим последовательность разностей: 0,9,18,27…81. Из 81 можно получить 90 или 99. Если взять 90 , то следующее должно быть 90+9=99 , но 99-(9+9)=81. Следовательно, после 81 идет 99 . А 99 можно получить уже из любого изначального целого числа из промежутка [100;109]