408 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
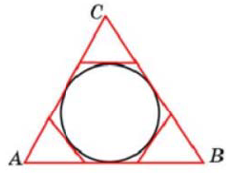
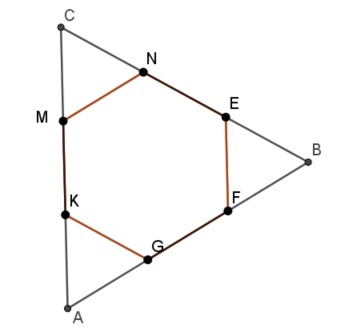
Задание 1
$$P_{\Delta MNC}=6$$
$$P_{\Delta FEB}=8$$
$$P_{\Delta AKG}=10$$
$$P_{\Delta ABC}=P_{\Delta MNC}+P_{\Delta FEB}+P_{\Delta AKG}$$
$$P_{\Delta ABC}=6+8+10=24$$
Задание 2
Площадь поверхности шара определяется формулой:
$$S=4\pi R^2$$
Соответственно, получаем суммарную площадь поверхности, равную:
$$S=4\pi7^2+4\pi24^2=4\cdot625\pi$$
Здесь число $$625=R^2_{\Sigma}$$ - квадрат радиуса шара, у которого площадь поверхности будет равна сумме площадей поверхностей двух данных шаров. Имеем:
$$R_{\Sigma}=\sqrt{625}=25$$
Задание 3
Эту задачу проще решать от обратного и вычислять вероятность промаха цели при одном, двух, трех и т.д. числу выстрелов. А, затем, взять противоположную вероятность, которая будет определять поражение цели. Имеем:
- 1 выстрел. Вероятность промаха: $$P=1-0,2$$, вероятность попадания: $$1-P=0,2$$;
- 2 выстрела. Вероятность промаха: $$P=(1-0,2)^2$$, вероятность попадания: $$1-P=0,36$$;
- 3 выстрела. Вероятность промаха: $$P=(1-0,2)^3$$, вероятность попадания: $$1-P=0,488$$.
То есть, стрелку нужно сделать 3 выстрела (минимум).
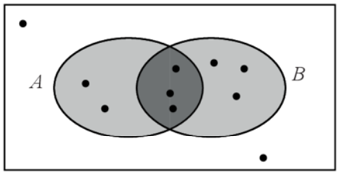
Задание 4
$$P(B|A)=\frac{P(BA)}{P(A)}$$ – по определению
$$P(A)=\frac{5}{10}$$ (всего 10 точек, 5 точек лежат в левом круге, т.е. принадлежат событию А)
$$P(BA)=\frac{3}{10}$$ (всего 3 точки принадлежат пересечению двух кругов)
$$P(B|A)=\frac{\frac{3}{10}}{\frac{5}{10}}=\frac{3}{5}=0,6$$
Задание 5
$$\sqrt{\frac{20+x}{x}}+\sqrt{\frac{20-x}{x}}=\sqrt{6}\Leftrightarrow\sqrt{\frac{20}{x}+1}+\sqrt{\frac{20}{x}-1}=\sqrt{6}$$.
Пусть $$\frac{20}{x}=t: \sqrt{t+1}+\sqrt{t-1}=\sqrt{6}\Rightarrow t+1+2\sqrt{t^2-1}+t-1=6\Rightarrow$$
$$\Rightarrow2t+2\sqrt{t^2-1}=6\Rightarrow\sqrt{t^2-1}=3-t\Rightarrow t^2-1=9-6t+t^2\Rightarrow$$
$$\Rightarrow 6t=10\Rightarrow t=\frac{5}{3}$$.
Обратная замена: $$\frac{20}{x}=\frac{5}{3}\Rightarrow x=12$$.
ОДЗ не писали, выполнили проверку, так проще.
Задание 6
$$(\frac{c}{2d^2})^{-6}:\frac{d^{18}}{c^6}=\frac{c^{-6}\cdot c^6}{2^{-6}d^{-12}\cdot d^{18}}=\frac{2^6}{d^6}=\frac{2^6}{\sqrt{2}^6}=\sqrt{2}^6=8$$.
Задание 8
Задание 9
Пусть $$V$$ - скорость движения вверх по реке, тогда $$1,04V$$ - по озеру.
Пусть $$t$$ - время по реке, тогда $$1,15t$$ - по озеру.
Получим:
$$S_1=Vt$$ - расстояние по реке
$$S_2=1,04V\cdot1,15t=1,196Vt=1,196S_1$$ - по озеру $$\Rightarrow$$ на $$19,6\%$$
Задание 10
Правый график уже, значит модуль коэффициента при $$x^2$$ у него больше, т.е. это $$f(x).$$
$$g(x)$$ проходит через $$(0;3),$$ значит $$c=3$$ и через $$(-1;1)$$ и $$(1;3).$$ Тогда:
$$\left\{\begin{matrix} 1=a\cdot(-1)^2+b\cdot(-1)+3\\ 3=a\cdot1^2+b\cdot1+3 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -2=a-b\\ 0=a+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2a=-2\\ 2b=2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=-1\\ b=1 \end{matrix}\right.$$
Получили $$g(x)=-x^2+x+3.$$ Тогда:
$$-2x^2+7x-2=-x^2+x+3\Rightarrow x^2-6x+5=0\Rightarrow\left[\begin{matrix} x=1\\ x=5 \end{matrix}\right.$$
Тогда $$B_x=5$$
$$g(5)=-5^2+5+3=-25+8=-17$$