372 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 2
Пусть $$O$$ – отличная погода, $$X$$ – хорошая
Всего четыре возможных варианта на 19,20,21 числа
$$XXO, XOO,OOO,OXO$$
$$P(A_1+A_2+A_3+A_4)=P(A_1)+P(A_2)+P(A_3)+P(A_4)=$$
$$=0,8\cdot0,8\cdot0,2+0,8\cdot0,2\cdot0,8+0,2\cdot0,8\cdot0,8+0,2\cdot0,2\cdot0,2=0,392$$
Задание 3
$$\angle ADB=\frac{138}{2}=59,$$ тогда $$\angle CDA=180−59=121$$
$$\angle DAE=\frac{38}{2}=19$$
$$ACB=180−121−19=40$$
Задание 4
$$2(\log_a b+log_a a^{\frac{1}{4}})+2\log_b a+0,5(\log_a a+\log_a b)=$$
$$=2\log_a b+0,5+\frac{2}{\log_a b}+0,5+0,5\log_a b$$
Пусть $$\log_a b=t$$
Тогда перепишется
$$2t+\frac{2}{t}+0,5t+1$$
Перейдем к тому, что дано
$$\log_{a^2b}\frac{b}{a}=\frac{1}{4}$$
$$\frac{\log_a\frac{b}{a}}{\log_a a^2b}=\frac{1}{4}$$
$$\frac{t−1}{t+2}=14$$
$$t=2$$
Подставляем и получаем ответ 6
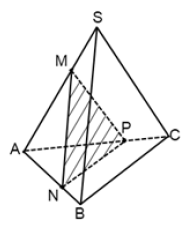
Задание 5
$$V_{SABC}=\frac{1}{3}S_{ABC}h=54$$
$$\Delta ABC$$ подобен $$\Delta ANP$$ по 2-м углам
$$k=\frac{3}{2}$$
$$S_{ANP}=\frac{S_{ABC}}{k^2}=\frac{4}{9}S_{ABC}$$
$$\Delta AMO_1$$ подобен $$\Delta ASO$$
$$\frac{MO_1}{SO}=\frac{2}{3}$$
$$MO_1=\frac{2}{3}h$$
$$V_{MANP}=\frac{1}{3}\cdot\frac{4}{9}\cdot S_{ABC}\cdot\frac{2}{3}h$$
Из условия $$V_{SABC}=54$$ можно легко найти объем 16
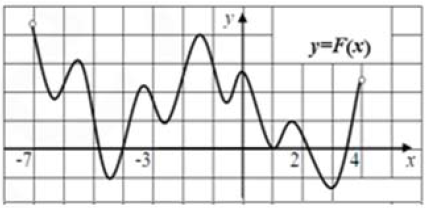
Задание 6
$$F'(x)=f(x)$$
Можно заметить, что точка $$x=0$$ - точка локального максимума функции
По геометрическому смыслу производной:
$$F'(0)=k=\tg\alpha=0$$
Задание 7
Задание 8
$$T_1=\frac{20}{3}$$ минуты или 400 с
$$T_2=\frac{4}{3}$$ минуты или 80 с
$$T_1V_1−T_1V_2=400$$
$$T_2V_1+T_2V_2=400$$
Откуда $$V_1=3 V_2=2$$
$$2\cdot3=6$$
Задание 9
Уравнение прямой $$y=kx+b$$
$$k=\tg\alpha$$
Легко найти из рисунка из прямоугольных треугольников, также легко найти коэффициент $$b$$ из рисунка или из уравнения
$$f(x)=2,5x+1,5$$
$$g(x)=-1,5x-3,5$$
Найдем точку пересечения:
$$2,5x+1,5=-1,5x−3,5$$
$$x=-1,25$$
Задание 10
В первом броске нас устраивает только очки: $$1,2,3,$$ если будет больше то бросать перестанем
$$A_1$$ Во-втором броске, если при первом броске выпало $$1,$$ то нас устраивает $$3,4,5,6,$$ чтобы перестать бросать дальше
$$A_2$$ Во-втором броске, если при первом броске выпало $$2,$$ то нас устраивает $$2,3,4,5,6$$
$$A_3$$ Во-втором броске, если при первом броске выпало $$3,$$ то нас устраивает $$1,2,3,4,5,6$$
$$P=\frac{1}{6}\cdot\frac{4}{6}+\frac{1}{6}\cdot\frac{5}{6}+\frac{1}{6}\cdot\frac{6}{6}\approx0,42$$
Задание 11
Найдем критические точки: $$(2x−8)e^{2−x}−(x^2−8x+8)e^{2−x}=0$$
$$e^{2−x}(2x−8−x^2+8x−8)=0$$
$$e^{2−x}\neq0$$
$$−x^2+10x−16=0$$
$$x=2$$ - точка минимума
$$x=8$$ - точка максимума
$$y(2)=−4$$