404 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.

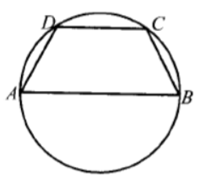
Рассмотрим треугольник ADC, в котором AD=DC по условию задания, а угол D равен:

$$\angle D=\frac{360^{\circ}-\angle A-\angle B}{2}=\frac{360^{\circ}-60^{\circ}-60^{\circ}}{2}=120^{\circ}.$$

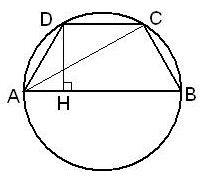
Найдем сторону AD=DC из треугольника ADH:

$$AD=\frac{AH}{\cos60^{\circ}}=\frac{(AB-DC):2}{0,5}=AB-DC$$

$$2AD=AB=18$$

$$AD=\frac{18}{2}=9$$

Радиус описанной окружности можно найти по теореме синусов для треугольника ADC, имеем:

$$R=\frac{AD}{2\sin\angle DCA}=\frac{9}{2\cdot\sin30^{\circ}}=9.$$

В основании правильной четырёхугольной призмы лежит правильный шестиугольник:

Найдем сторону этого шестиугольника из треугольника, у которого известен угол 120 градусов между сторонами и противолежащая сторона $$D = 2\sqrt{3}.$$ По теореме косинусов можно записать:

$$D^2=a^2+a^2-2\cdot a\cdot a\cdot\cos120$$

$$(2\sqrt{3})^2=2a^2-2a^2\cdot(-\frac{1}{2})$$

$$12=3a^2$$

$$a=2$$

Площадь боковой поверхности правильной шестиугольной призмы со стороной a = 2 и высотой h = 3, равна:

Площадь боковой поверхности правильной призмы со стороной a = 6 и высотой h = 2, равна:

$$S=6\cdot a\cdot h=6\cdot2\cdot2=24$$

Цифры меняются от 0 до 9, значит, совпадение трех последних цифр – это одно из $$m = 10$$ событий:

$$000, 111, 222, …, 999.$$

Всего возможных комбинаций из трех цифр $$n=10^3=1000.$$ Получаем значение искомой вероятности:

$$P=\frac{m}{n}=\frac{10}{1000}=0,01$$

Пусть первое число - результат первого броска, второе - второго, третье - третьего. Тогда возможные варианты превысить число 9 в сумме за три броска:

1 3...6 6 - четыре исхода: $$\frac{1}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}\cdot4=\frac{4}{216}$$

1 4...6 5 - три исхода: $$\frac{1}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}\cdot3=\frac{3}{216}$$

1 5...6 4 - два исхода: $$\frac{1}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}\cdot2=\frac{2}{216}$$

1 6 3 - один исход: $$\frac{1}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}=\frac{1}{216}$$

Аналогично рассматривается с первой двойкой (15 исходов всего $$\frac{15}{216}$$), тройкой - 21 исход $$\frac{21}{216}$$

4 1...5 6 - 5 исходов: $$\frac{5}{216}$$

4 1...5 5 - 5 исходов: $$\frac{5}{216}$$

4 2...5 4 - 4 исхода: $$\frac{4}{216}$$

4 3...5 3 - 3 исхода: $$\frac{3}{216}$$

4 4...5 2 - 2 исхода: $$\frac{2}{216}$$

4 5 1 - 1 исход: $$\frac{1}{216}$$

Заметьте, что 4 6 не рассматриваем уже, т.к. тогда на втором броске уже будет больше 9.

Аналогично с пятеркой: 18 исходов: $$\frac{18}{216}$$ и шестеркой: 15 исходов: $$\frac{15}{216}$$

В итоге получили: $$10+15+21+20+18+15=99$$ исходов с вероятность $$\frac{1}{216}$$

$$P(A)=\frac{99}{216}=0,458(3)\approx0,46$$

Учтём, что $$\log_8\sqrt{x^2}=\log_8|x|.$$ Так как есть $$\log_8(-x),$$ то $$-x>0\Rightarrow x<0.$$ Тогда $$\log_8|x|=\log_8(-x)$$

Пусть $$\log_8(-x)=y.$$ Получим: $$\sqrt{2y}=y\Rightarrow\left\{\begin{matrix} 2y=y^2\\ y\geq0 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} y=0\\ y=2 \end{matrix}\right.$$

Обратная замена:

$$\left[\begin{matrix} \log_8(-x)=0\\ \log_8(-x)=2 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} -x=1\\ -x=64 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} x=-1\\ x=-64 \end{matrix}\right.$$

Сумма корней $$(-1)+(-64)=-65.$$

$$\frac{p(b)}{p(\frac{1}{b})}=\frac{(b+\frac{3}{b})(3b+\frac{1}{b})}{(\frac{1}{b}+3b)(\frac{3}{b}+b)}=1$$

Приравниваем производные и функции:

$$\left\{\begin{matrix} (x+7)'=(ax^2-15x+15)'\\ x+7=ax^2-15x+15 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1=2ax-15\\ ax^2-16x+8 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x=\frac{8}{a}\\ a\cdot\frac{64}{a^2}-\frac{16\cdot8}{a}+8=0 \end{matrix}\right.$$

$$\frac{64}{a}-\frac{128}{a}=-8\Rightarrow -\frac{64}{a}=-8\Rightarrow a=8$$

Чем выше скорость вращения, тем больше давление воды ⇒ нужно найти минимальную скорость, давление должно быть равно 0.

$$m(\frac{v_2}{0,625}-10)=0$$

Произведение равно 0, когда один из множителей равен 0. m ≠ 0

$$\frac{v_2}{0,625}-10=0$$

$$\frac{v_2}{0,625}=10$$

$$v_2 = 10\cdot0,625$$

$$v_2 = 6,25$$

$$v = 2,5$$

Пусть производительность третьего рабочего $$x$$ раб/мин, тогда производительность первого рабочего - $$(x+0,2x)=1,2x$$ раб/мин, а производительность третьего считаем по пропорции

1,2x - 90%

пр.тр. - 100%

пр.тр. $$=\frac{1,2x\cdot100}{90}=\frac{4x}{3}$$ - производительность третьего рабочего.

Всю работу примем за 1. Тогда время на выполнение работы первым рабочим $$\frac{1}{1,2x}$$ минут, третьим - $$\frac{1}{x}$$ минут. Первый рабочий выполнил работу на 6 минут быстрее третьего. Составим и решим уравнение:

$$\frac{1}{x}-\frac{1}{1,2x}=6$$

$$\frac{6-5}{6x}=6$$

$$\frac{1}{6x}=6$$

$$36x=1$$

$$x=\frac{1}{36}$$ раб/мин - производительность третьего рабочего, значит, всю работу он выполнит за 36 минут.

$$\frac{4}{3}\cdot\frac{1}{36}=\frac{1}{27}$$ раб/мин - производительность второго рабочего, значит, всю работу он выполнит за 27 минут.

$$36-27=9$$ минут - на столько дольше работу выполняет третий рабочий, чем второй.

Если второй выполнил работу на 2 минуты раньше третьего, то

$$9-2=7$$ минут - на столько позже третьего второй начал работу.

График проходит через (-4;1) и (-1;3). Получим:

$$\left\{\begin{matrix} 1=b+\log_a\frac{1}{4}\\ 3=b+\log_a 1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} \log_a\frac{1}{4}=-2\\ b=3 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=2\\ b=3 \end{matrix}\right.$$

Получили $$f(x)=3+\log_2(-\frac{1}{x})=5\Rightarrow \log_2(-\frac{1}{x})=2\Rightarrow -\frac{1}{x}=4\Rightarrow x=-0,25$$