356 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Больше разборов на моем ютуб-канале
Задание 1
Составим систему исходя из условия
$$\left\{\begin{matrix} 60\cdot x+75\cdot y=270000\\ 60\cdot 0,85\cdot x+75\cdot 0,9y=237000 \end{matrix}\right.$$
Решая ее $$(x,y)=(2000,2000)$$
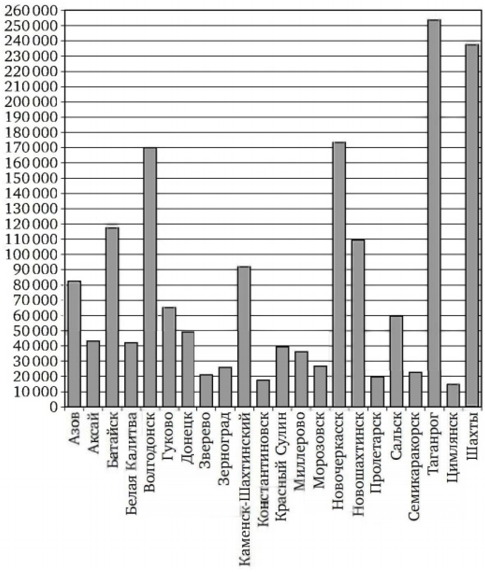
Задание 2
Считаем столбики, где население меньше 50000, таких всего 12.
Задание 3
Легко увидеть, что полукруги сбоку встают на пустые места.
В итоге получаем прямоугольник и квадрат.
$$S=7\cdot4+0,5\cdot4\cdot3=34$$
Задание 4
Всего монет 20.
Вероятность взятия пятирублевой монеты $$\frac{8}{20}$$, вероятность выпадения решки $$\frac{1}{2}$$
$$P(A)=\frac{8}{20}\cdot\frac{1}{2}=0,2$$
Задание 5
Сделаем замену
$$5^{\lg x}=a>0,\quad 3^{\lg x}=b>0$$
$$a−\frac{1}{3b}=3b−\frac{1}{5a}$$ Поделим все на $$b>0$$
И сделаем новую замену $$\frac{a}{b}=z>0$$
$$z=\frac{25}{9}$$
Обратная замена:
$$\frac{5^{\lg x}}{3^{\lg x}}=\frac{25}{9}$$
Отсюда ответ очевиден.
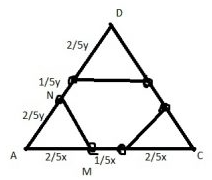
Задание 6
Треугольник AMN подобен ADC с коэффициентом подобия $$k=\frac{x}{\frac{2}{5}x}=2,5$$
$$S_{AMN}=\frac{100}{2,5^2}=16$$
Аналогично с остальными двумя (очевидно, что они будут равны)
В итоге $$S_{шест}=100−3\cdot16=52$$
Задание 7
Составим уравнение исходя из геометрического смысла производной
$$−3=3x^2+14x+8$$
Откуда
$$x=−1$$
$$x=−\frac{11}{3}$$
Подставим $$x=−1$$ в первую и во вторую функцию чтобы найти ординату (она должна быть одинаковой)
$$y=−7$$
При $$x=−\frac{11}{3}$$ ординаты будут разными.
$$-1+(-7)=-8$$
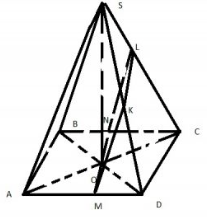
Задание 8
Построим сечение параллельное грани ABS и продящее через центр
Проводим через точку O прямую параллельную AB, далее строим две прямые параллельные боковым ребрам (NL и MK) и соединяем KL как точки лежащие в одной плоскости.
Искомое сечение – р\б трапеция
$$MN=120, LK=60$$ – как средняя линия
Дальше сторону можно найти из теоремы Пифагора
$$MK=NL=10\sqrt{34}$$
Далее легко ищется площадь р\б трапеции
Задание 9
$$1000\cdot\cos12^{\circ}\cdot\cos24^{\circ}\cdot\cos36^{\circ}\cdot\cos48^{\circ}\cdot\cos60^{\circ}\cdot\cos72^{\circ}\cdot\cos84^{\circ}$$
Умножим и поделим на $$\sin12^{\circ}$$.
$$\frac{1000\sin12\cos12...\cos84}{\sin12}=\frac{500\sin24\cos24...\cos84}{\sin12}=$$
$$=\frac{250\sin48\cos36\cos48...\cos84}{\sin12}=\frac{125\sin96\cos36\cos60\cos72\cos84}{\sin12}$$.
Учтём, что
$$\cos36\cos72=\frac{\sin36\cos36\cos72}{\sin36}=\frac{\sin72\cos72}{2\sin36}=\frac{\sin144}{4\sin36}=\frac{\sin(180-36)}{4\sin36}=$$
$$=\frac{\sin36}{4\sin36}=\frac{1}{4}$$.
При этом $$\sin96=\sin(180-84)=\sin84$$.
Тогда $$\sin84\cos84=\frac{\sin168}{2}=\frac{\sin12}{2}$$.
Получим: $$\frac{125\cdot\sin12\cdot\frac{1}{2}\cdot\frac{1}{4}}{2\sin12}=\frac{125}{16}=7,8125$$.
Задание 10
$$256^{\frac{7}{5}}=2^7\cdot V_2^{\frac{7}{5}}$$
Возведем обе части уравнения в степень $$\frac{5}{7}$$, получим:
$$256=(2^7)^{\frac{5}{7}}V_2$$
$$V_2=\frac{256}{32}=8$$
Задание 11
Пусть $$p>5$$ – производительность мастера
Составим уравнение:
$$pt=2(p−2)\cdot(t−1)$$
$$(p−4)(t−2)=4$$
Нужно подобрать такие $$p$$ и $$t$$, чтобы выполнялось равенство
$$p−4=2$$ и $$t−2=2$$
$$p=6$$ и $$t=4$$
$$p>5$$ – верно, значит $$6\cdot4=24$$
Задание 12
$$y'=\frac{3\cdot(2x+5)}{(x^2+5x+7)^2}=0$$
$$x=−2,5$$ – точка максимума по методу интервалов
$$y(-2,5)=4$$