ЕГЭ математика 2018. Разбор варианта Алекса Ларина № 206
Решаем ЕГЭ вариант Ларина № 209. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,13,14,15 заданий тренировочного варианта ЕГЭ Ларина № 206 (alexlarin.com)
Решаем ЕГЭ вариант Ларина № 209. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина № 206 (alexlarin.com)
Задание 1
По результатам приемной кампании 2017 года, в вузы на бюджетные места поступили 6202 победителя и призера олимпиад. В 2016 году этот показатель составлял 5950 человек. На сколько процентов был превышен показатель поступивших в вузы на бюджетные места победителей и призеров олимпиад в 2017 году по сравнению с 2016 годом? (Ответ округлите до целого числа процентов).
5950 - 100 % 6202 - x $$x=\frac{6202\cdot100}{5950}=104,235254\approx104$$ % $$104-100=4$$ %
Задание 2
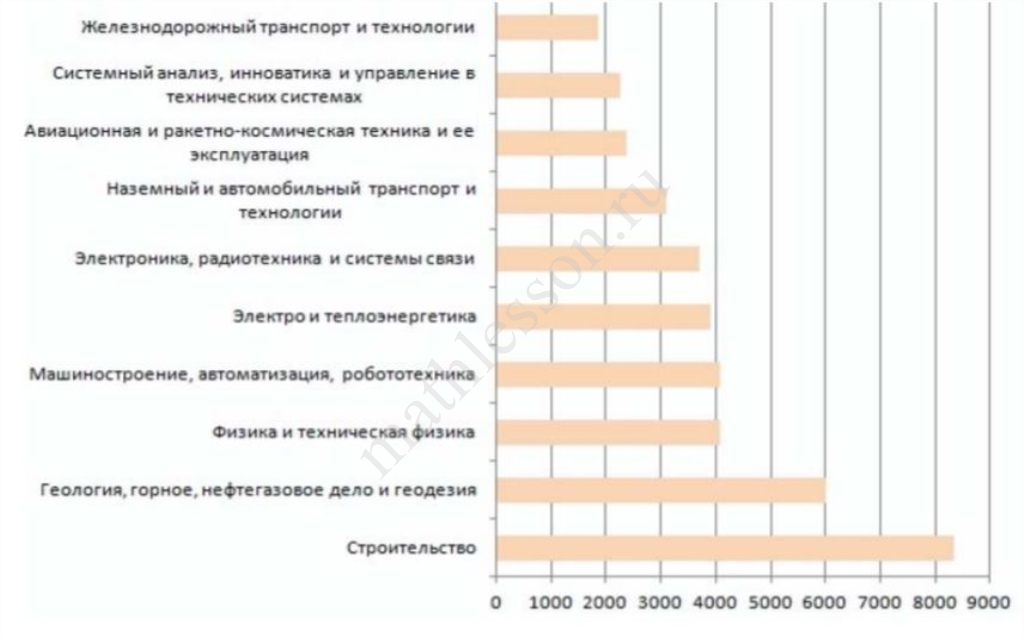
В период с 12 июня по 13 июля 2017 года тест шансов на портале Поступи Онлайн
прошло более миллиона абитуриентов. На рисунке показано распределение
количества результатов теста шансов поступления на технические специальности вузов. Определите по рисунку количество абитуриентов, принявших участие в тестировании, имеющих шансы поступить на специальности «Геология, горное,
нефтегазовое дело и геодезия».
Задание 3
Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
$$S=\frac{2+5}{2}\cdot4=14$$
Задание 4
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,1, а при каждом последующем – 0,9. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,95?
| Выстрел | Попал | Промахнулся |
| 1 | 0,1 | 0,9 |
| 2 | 0,9 | 0,1 |
| 3 | 0,9 | 0,1 |
| n | 0.9 | 0.1 |
Чтобы решить задание, мы будем рассматривать противоположное событие - мишень ниразу не поражена. То есть, если нам надо получить вероятность поражения больше, чем 0,95, то вероятность промаха будет меньше, чем 1-0,95=0,05. Первый выстрел промахивается с вероятностью 0,9, второй - 0,1. Значит, вероятность того, что два раза подряд промахнется 0,9*0,1, три раза = 0,9*0,1*0,1 и тд. А n раз $$= 0,9*0,1^{n-1}$$
$$0,9\cdot 0,1^{n-1}\leq 0,05$$
$$0,1^{n-1}\leq 0,0(5)$$
$$\Rightarrow n-1\leq 2$$
$$\Rightarrow n\leq 3$$
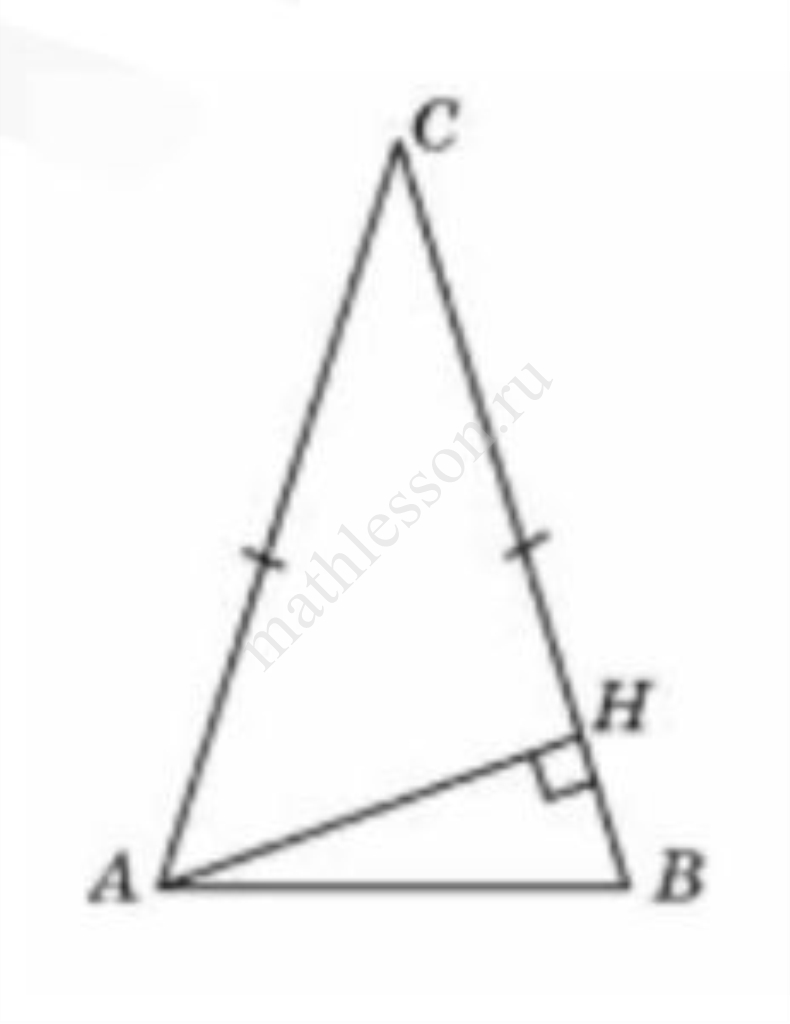
Задание 5
из $$\bigtriangleup ACH:$$ $$AH=\frac{AC}{2}=\frac{4}{2}=2$$ (катет напротив угла в $$30^{\circ}$$)
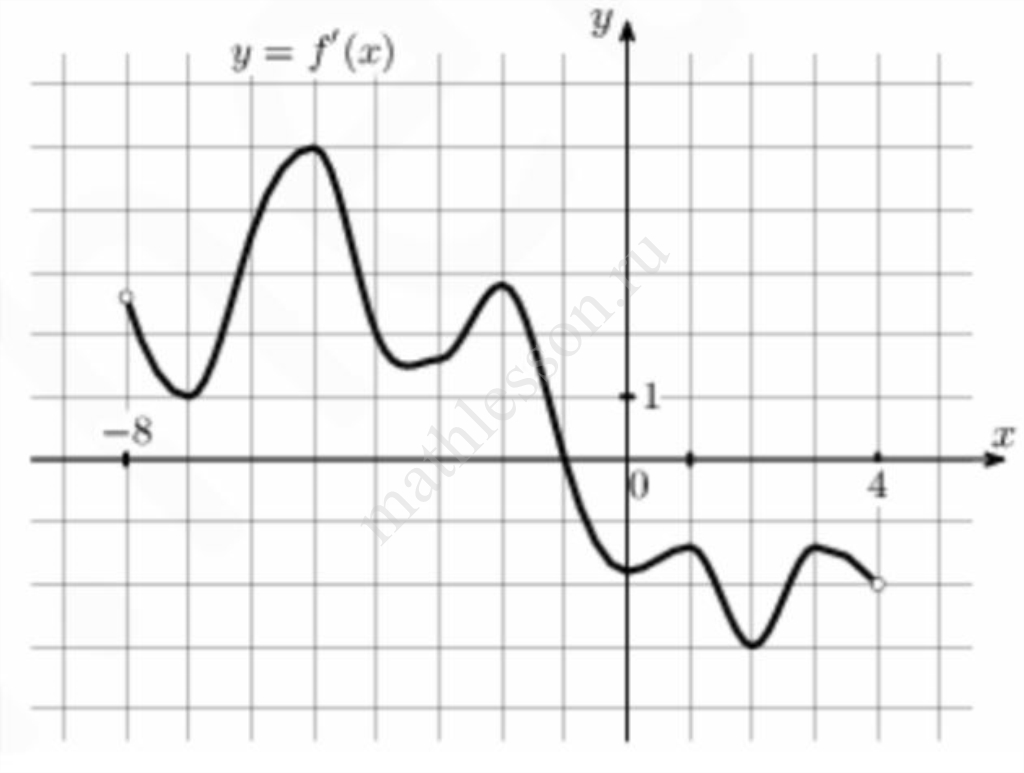
Задание 6
На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (-8;4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
На всем отрезке [-7; -3] f'(x) $$\Rightarrow$$ функция возрастает минимальное значение в начале отрезка $$\Rightarrow$$ -7
Задание 7
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Пусть х - третье ребро $$2\cdot3x+2\cdot4x+2\cdot3\cdot4=94$$ $$6x+8x+24=94$$ $$\Leftrightarrow$$ $$14x=70$$ $$\Leftrightarrow$$ $$x=5$$
Задание 8
Найдите значение выражения $$-18\sqrt{2}\sin (-135^{\circ})$$
$$-18\sqrt{2}\sin (-135^{\circ})=18\sqrt{2}\sin 135^{\circ}=$$ $$18\sqrt{2}\sin (90^{\circ}+45^{\circ})=18\sqrt{2}\cos 45^{\circ}=18\sqrt{2}\frac{\sqrt{2}}{2}=18$$
Задание 9
Высота над землeй подброшенного вверх мяча меняется по закону $$h(t)=1,6+8t-5t^{2}$$, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
$$h(t)=1,6+8t-5t^{2}\geq3$$ $$-5t^{2}+8t-1,4\geq0$$ $$5t^{2}-8t+1,4\leq0$$ $$D=64-28=36$$ $$t_{1}=\frac{8+6}{10}=1,4$$ $$t_{1}=\frac{8-6}{10}=0,2$$ $$1,4-0,2=1,2$$
Задание 10
На направление «Фундаментальная и прикладная лингвистика» от выпускников лицеев подано на 600 заявлений больше, чем от выпускников гимназий. Девушек среди выпускников лицеев в 5 раз больше, чем девушек среди выпускников гимназий. А юношей среди выпускников лицеев больше, чем юношей среди выпускников гимназий в n раз, причем 6 < n < 12 (n ‐ целое число). Определить общее количество заявлений, если среди выпускников гимназий юношей на 20 больше, чем девушек.
| Всего | Девушки | Юноши | |
| Лицеи: | х+600 | 5у | n(x-y) |
| Гимназии: | x | y | x-y |
$$6< n< 12$$
$$x-y-y=20$$ $$\Rightarrow x-2y=20\Rightarrow x=20+2y$$
$$5y+n(x-y)=x+600$$
$$5y+n(20+2y-y=20+2y+600$$
$$5y+20n+ny-20-2y-600=0$$
$$3y+ny=620-20n$$
$$y=\frac{620-20n}{3+n}$$
n принадлежит промежутку от 6 до 12 и является натуральными числом, при этом у тоже число натуральное. Подставим все числа из промежутка от 6 до 12 (без 6 и 12) в полученное выражение и проверим, где у получается натуральным. А получается при n=7, y=48. Тогда x=20+2*48=116 и всего учеников: x+x+600=116+116+600=832
Задание 11
Найдите наименьшее значение функции $$y=\sqrt{x^{2}+8x+25}$$
$$y=\sqrt{x^{2}+8x+25}$$ $$x_{0}=-\frac{8}{2}=-4$$ - вершина $$y_{min}=\sqrt{(-4)^{2}+8(-4)+25}=\sqrt{16-32+25}=\sqrt{9}=3$$
Задание 12
а) Решите уравнение $$\sin (2x+\frac{\pi}{2})=\cos(x+\frac{\pi}{2})+\sin(x+\frac{\pi}{2})$$
б) Укажите корни этого уравнения, принадлежащие отрезку [$$-\frac{3\pi}{2}; 0$$]
$$\sin (2x+\frac{\pi}{2})=\cos(x+\frac{\pi}{2})+\sin(x+\frac{\pi}{2})$$ [$$-\frac{3\pi}{2}; 0$$] $$\cos 2x=-\sin x+\cos x$$ $$\cos ^{2}x-\sin^{2} x+\sin x-\cos x=0$$ $$(\cos x-\sin x)(\cos x+\sin x)-(\cos x-\sin x)=0$$ $$(\cos x-\sin x)(\cos x+\sin x-1)=0$$ $$\left\{\begin{matrix}\cos x=\sin x\\\cos x+\sin x-1=0\end{matrix}\right.$$ $$\cos x=1-2\sin ^{2}\frac{x}{2}$$ $$\left\{\begin{matrix}1=\tan x\\1-2\sin^{2}\frac{x}{2}+2\sin\frac{x}{2}\cos \frac{x}{2}-1=0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{4}+\pi n (n\in Z)\\2\sin\frac{x}{2}(\cos\frac{x}{2}-\sin\frac{x}{2})=0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{4}+\pi n(n\in Z)\\\sin\frac{x}{2}=0\\\cos\frac{x}{2}-\sin\frac{x}{2}=0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{4}+\pi n(n\in Z)\\\frac{x}{2}=\pi n\\\tan\frac{x}{2}=1\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{4}+\pi n(n\in Z)\\x=2\pi n(n\in Z)\\\frac{x}{2}=\frac{\pi}{4}+\pi n\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{4}+\pi n(n\in Z)\\x=2\pi n(n\in Z)\\x=\frac{\pi}{2}+2\pi n(n\in Z)\end{matrix}\right.$$
Задание 13
Точки М, N и К принадлежат соответственно ребрам АD, AB и BC тетраэдра ABCD, причем АМ : МD = 2 :3, ВN : АN = 1 : 2, ВК = КС.
а) Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K.
б) Найдите отношение, в котором секущая плоскость делит ребро CD.
а) В и М $$\in$$ (ABD) - соединяем В и K $$\in$$ (ABC) - соединяем $$BK\cap AC=P$$ M и P $$\in$$ (ADC) - соединяем $$\Rightarrow$$ $$MP\cap DC=Q$$ $$\Rightarrow$$ MQKN - искомая плоскость.
б) 1. Проведем $$CO\parallel AB\Rightarrow \bigtriangleup BKN\sim \bigtriangleup COK$$ $$\Rightarrow$$ $$\frac{BN}{CO}=\frac{BK}{CK}=\frac{NK}{KO}$$ $$\bigtriangleup POK\sim \bigtriangleup PNA$$ $$\Rightarrow$$ $$\frac{PC}{CA}=\frac{CO}{AN}=\frac{PO}{PN}$$
2. Возьмем $$\frac{BN}{CO}=\frac{BK}{CK}$$ и $$\frac{PC}{PA}=\frac{CO}{AN}$$ и умножим $$\frac{BN}{CO}\cdot\frac{CO}{AN}=\frac{BK}{CK}\cdot\frac{PC}{AP}$$ $$\Rightarrow$$ $$frac{BN}{AN}=\frac{BK}{CK}\cdot\frac{PC}{AP}$$ $$\Rightarrow$$ $$\frac{y}{2y}=\frac{z}{z}\cdot\frac{PC}{AP}$$ $$\Rightarrow$$ $$\frac{PC}{AP}=\frac{1}{2}$$
3. Аналогично $$\frac{DM}{AM}=\frac{CP}{AP}\cdot\frac{DQ}{QC}$$ $$\Rightarrow$$ $$\frac{3x}{2x}=\frac{1}{2}\cdot\frac{DQ}{QC}$$ $$\Rightarrow$$ $$\frac{DQ}{QC}=\frac{3}{1}$$
Задание 15
Диагонали $$AC$$ и $$CE$$ правильного шестиугольника $$ABCDEF$$ разделены точками $$M$$ и $$N$$ так, что $$AM:AC=CN:CE$$ и точки $$B$$, $$M$$ и $$N$$ лежат на одной прямой.
Задание 16
Митрофан хочет взять в кредит 1,7 млн. рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Митрофан взять кредит, чтобы ежегодные выплаты были не более 300 тысяч рублей?
Задание 18
Три числа назовём хорошей тройкой, если они могут быть длинами сторон треугольника. Три числа назовём отличной тройкой, если они могут быть длинами сторон прямоугольного треугольника.