311 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
Решаем ЕГЭ 311 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №311 (alexlarin.com)
ВАЖНО: ТЕПЕРЬ РЕШЕНИЕ КАЖДОГО ЗАДАНИЯ РАСПОЛОЖЕНО ПОД ТЕКСТОМ САМИХ ЗАДАНИЙ! ВИДЕО НАЧИНАЕТСЯ С МОМЕНТА РЕШЕНИЯ САМОГО ЗАДАНИЯ. ЕСЛИ НУЖНО НАЧАТЬ ЗАНОВО, И ЛЕНЬ КРУТИТЬ, ПРОСТО ПЕРЕЗАГРУЗИТЕ СТРАНИЦУ. ТАК ЖЕ ДЛЯ НЕКОТОРЫХ ЗАДАНИЙ ПРЕДСТАВЛЕНЫ PDF РЕШЕНИЯ , ИНОГДА ОНИ НЕМНОГО ДОЛГО ГРУЗЯТСЯ
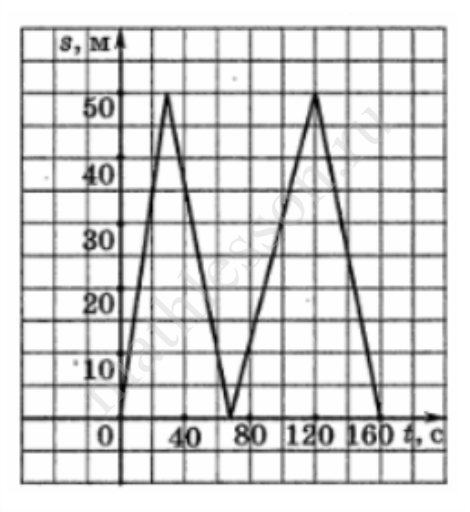
Задание 2
На тренировке в 50‐метровом бассейне пловец проплыл 200‐метровую дистанцию. На рисунке изображен график зависимости расстояния (в метрах) между пловцом и точкой старта от времени движения t (в секундах) пловца. Определите по графику, какое расстояние преодолел пловец за 2 мин 20
Задание 10
Водолазный колокол, содержащий $$\vartheta=3$$ моль воздуха при давлении $$p_{1}=1,8$$ атмосферы, медленно опускают на дно водоема. При этом происходит сжатие воздуха до конечного давления $$p_{2}$$. Работа, совершаемая водой при сжатии воздуха, определяется выражением $$A=\alpha \vartheta T\log_{2}\frac{p_{2}}{p_{1}}$$ , где $$\alpha=7,9$$ Дж/(моль*К) ‐ постоянная, T=300 K ‐ температура воздуха. Найдите, какое давление $$p_{2}$$ (в атмосферах) будет иметь воздух в колоколе, если при сжатии воздуха будет совершена работа в 14 220 Дж.
Задание 11
Поезд отправился со станции А, проследовал через станции В и С, прибыл на станцию D. Пусть ВС больше АВ на 1/4 часть АВ, а CD на 60% меньше ВС. Найдите среднюю скорость поезда на пути AD, если его скорость на АВ, ВС и CD равнялась соответственно 80 км/ч, 100 км/ч, 180 км/ч. Ответ дайте в км/ч.
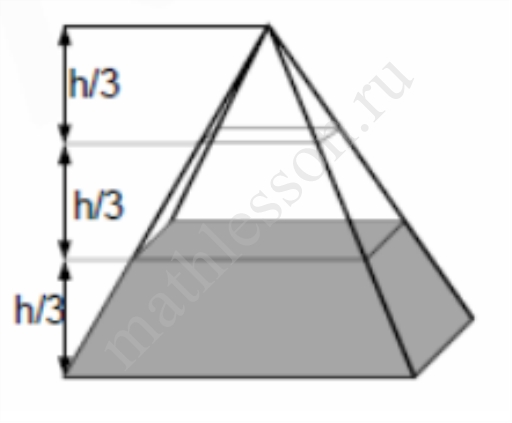
Задание 14
В правильной четырехугольной пирамиде плоскость $$\alpha$$, проведенная через сторону основания, делит двухгранный угол при основании пирамиды и боковую поверхность пирамиды пополам.
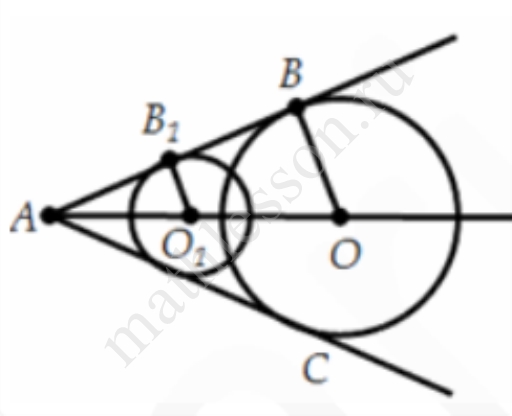
Задание 16
В трапеции ABCD (AD – нижнее основание) площади треугольников ABD и BDC равны соответственно 12 и 4, а точка G является серединой BD. Ниже прямой AD выбрана точка Е, АЕ=BD, а на отрезке ЕС выбрана точка F такая, что CF в 4 раза короче СЕ.
Задание 17
В июле планируется взять кредит в банке на сумму 1,6 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж в 2 раза больше наименьшего?
Задание 18
Найдите все значения параметра a, при каждом из которых наименьшее значение функции $$f(x)=-x^{4}+\frac{2ax^{3}}{9}+\frac{a^{2}x^{2}}{3}$$ на отрезке [-1;0] не превышает единицы и достигается на левом конце отрезка.
Задание 19
Имеются два многочлена от целочисленной переменной x :
Рассмотрим функцию $$f(x)=\frac{p(x)}{q(x)}$$ от целочисленной переменной x , определенную для тех значений x , для которых $$q(x)\neq 0$$