349 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Больше разборов на моем ютуб-канале
Задание 1
$$S=Vt$$
$$V_{ср}=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}$$
$$V_{ср}=\frac{200+180+140}{\frac{200}{90}+\frac{180}{40}+\frac{140}{120}}=80$$
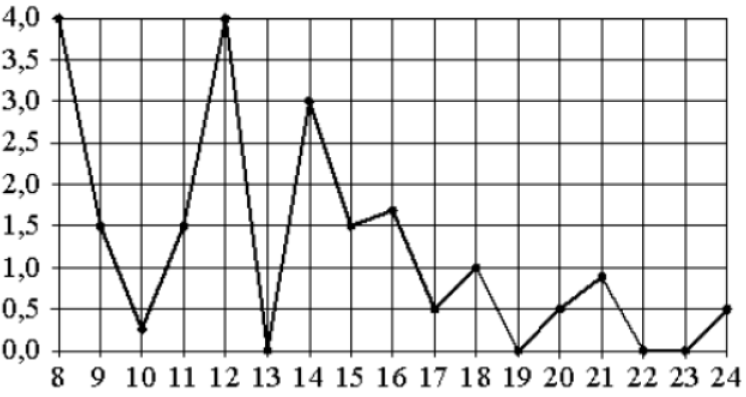
Задание 2
Находим слева 1,5 и двигаемся по прямой вправо, первая точка будет 9-го января.
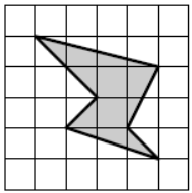
Задание 3
Легче всего здесь использовать формулу Пика.
$$S=В+\frac{Г}{2}-1$$, где B – кол-во точек внутри многоугольника, Г – кол-во точек на границе
$$В=4, Г=7$$
$$S=4+3,5−1=6,5$$
Задание 4
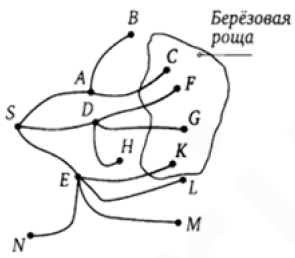
Стандартная лёгкая задача.
$$P(Z)=\frac{m}{n}$$, где m - количество положительных исходов, а n - всего
$$P(M)=\frac{1}{3}\cdot\frac{1}{4}=\frac{1}{12}\approx0,08$$
Задание 5
$$3^x\cdot7^{2x+3}=3\cdot7^{x-1}\cdot3^{x-1}\cdot7^{7-x}$$
$$3^{x-1}\cdot7^{2x+3}=3^{x-1}\cdot7^6$$
$$7^{2x+3}=7^6$$
$$2x+3=6$$
$$x=1,5$$
Задание 6
Параллельные прямые делят стороны угла на пропорциональные отрезки, значит
$$\frac{AP}{PK}=\frac{BO}{OK}$$ и $$\frac{KN}{NC}=\frac{OK}{BO}$$
Запишем
$$\frac{KN}{NC}=\frac{5}{4}=\frac{6}{NC}$$
$$NC=4,8$$
Задание 7
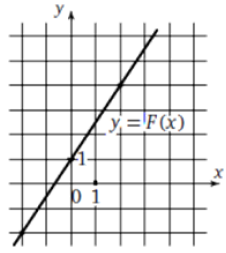
Пусть на рисунке изображена функция $$F(x)$$
По условию, $$f(x)=F'(x)$$
Т.е. нам дана производная функции
$$f(2)=F'(2)=k=\tg\alpha=\frac{3}{2}=1,5$$
Задание 8
$$V_1=πR^2h=π15^2h$$
$$V_2=π(\frac{15}{2})^2h$$
Видим, что объем второй кастрюли в 4 раза меньше объема первой, значит, нам потребуются 4 маленькие кастрюли.
Задание 9
$$\log_2^{\frac{1}{4}}4=4\log_2 4=8$$
$$\log_{13}39−\log^{−1}_3 13=\log_{13}39−\log_{13}3=\log_{13}13=1$$
Задание 10
$$v=2\cdot\sin\frac{2π7}{8}=2\sin\frac{7π}{4}=-2\frac{1}{\sqrt{2}}=-\sqrt{2}$$
$$E=\frac{0,38\cdot(-\sqrt{2})^2}{2}=0,38$$
Задание 11
5 ч 5 мин = 305 мин
12 ч 55 мин = 775 мин
4 ч 6 мин = 246 мин
Пусть товарный шёл $$t$$ ч до встречи $$\Rightarrow\left\{\begin{matrix} tV_1=246V_2\\ 775V_1=(t-305)V_2 \end{matrix}\right.$$
Поделим одно на другое.
$$\frac{t}{775}=\frac{246}{t-305}\Rightarrow t^2-305t=246\cdot775$$
$$t^2-305t-246\cdot775=0$$
$$\left\{\begin{matrix} \left[\begin{matrix} t_1=-310\\ t^2=615 \end{matrix}\right.\\ t>0 \end{matrix}\right.\Rightarrow t=615$$
$$615+775=1390$$
Задание 12
Найдем критические точки:
$$y'=\frac{3x}{\sqrt{3x^2+4}}-\frac{3x}{\sqrt{3x^2}}=0$$
Т.е. отрезок $$[0;3]$$, то
$$y'=\frac{3x}{\sqrt{3x^2+4}}-\sqrt{3}=0$$ – данное уравнение решений не имеет (проверьте сами)
Значит, наибольше значение будет достигаться на границах, очевидно, что в точке $$x=0$$
$$y(0)=2$$