346 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Больше разборов на моем ютуб-канале
Задание 1
Из условия составим систему:
$$\left\{\begin{matrix} С+Н=92\\ С+К=95\\ Н+К=97 \end{matrix}\right.$$
Нам нужно найти $$С+Н+К$$.
Сложим все уравнения и разделим на 2:
$$2С+2Н+2К=284$$
$$С+Н+К=142$$
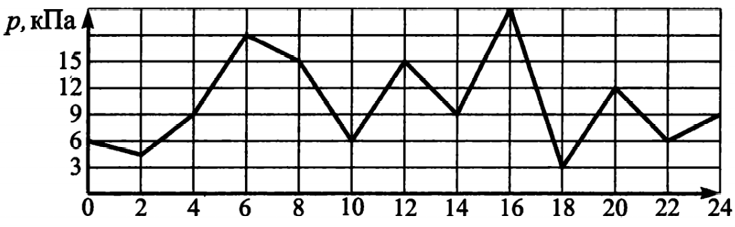
Задание 2
Минимально было 3 кПа, значит, ищем на графике 9 кПа, таких 8.
Задание 3
Пусть длина маленького отрезка $$x$$
Из прямоугольных треугольников
$$\tg a=\frac{6}{2+x}$$
$$\tg a=\frac{5}{2-x}$$
$$\frac{6}{2+x}=\frac{5}{2-x}$$
$$x=0,18$$
$$AO=2+0,18=2,18$$
Задание 4
Рассмотрим противоположное событие: что абонент позвонил в более чем 4 места.
$$P(B)=\frac{9}{10}\cdot\frac{8}{9}\cdot\frac{7}{8}\cdot\frac{6}{7}=0,6$$
(всего цифр 10, одна правильная цифра, 9 неправильных цифры – изначально).
Соответственно, когда абонент один раз набрал неправильный номер, то эту цифру исключаем, поэтому количество событий будет уменьшаться на 1.
$$P_{иск}=1-P(B)=0,4$$
Задание 5
ОДЗ рассматривать не надо, т.к. уже по условию корень равен положительному числу.
Возведем все в квадрат:
$$x^4-10x|x|+25=16$$
Тут стандартно рассматриваем два случая
1) $$x\geq0$$
$$x^4-10x^2+9=0$$ – решается стандартно, заменой $$x^2=t$$
$$x=-3,-1,1,3$$
2) $$x<0$$
$$x^4+10x^2+9=0$$ – тут $$D<0$$ нет корней
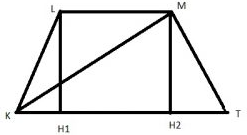
Задание 6
$$S=\frac{LM+KT}{2}\cdot MH_2$$
$$KH_1=TH_2=\frac{KT-LM}{2}$$ – по свойству р\б трапеции
$$KH_2=KT-TH_2=KT-\frac{KT-LM}{2}=\frac{LM+KT}{2}$$
Из $$KMH_2$$:
$$MH_2=\sin75°\cdot KM=8sin75°$$
$$KH_2=8\cos75°$$
$$S=KH_2\cdot MH_2=64\sin75°\cdot\cos75°=32\sin150°=32\sin(180°-30°)=$$
$$=32\sin30°=16$$
Задание 7
Точка минимума там, где производная меняет свой знак с – на +.
Таких точке на отрезке [2;-7] – 2 штуки (x=4, x=7). Но так как нас просят указать на интервале (-2;7), то x=7 отпадает.
Задание 8
Радиус шара совпадает с радиусом основания окружности в цилиндре.
$$V_ш=\frac{4}{3}πR^3=2021$$
$$V_ц=S_{осн}\cdot h=πR^2\cdot2R=2\pi R^3$$
Исходя из этого можно легко получить объем цилиндра (можно выразить πR3 из 1-го)
$$2\pi R^3=2021:\frac{2}{3}=3031,5$$
Задание 9
Так как тангенс и котагенс – взаимообратные функции, то
$$\tg^272°\cdot\ctg^254°=\tg^272\tg^254=\frac{\sin^272\cdot\cos^254}{\cos^272\cdot\sin^254}$$
Разберемся с $$\sin(54)=\sin(90−54)=\cos(36)$$
Аналогично $$\cos(54)=\sin(36)$$
$$\frac{sin^272\cdot\sin^236}{\cos^272\cdot\cos^236}$$
Заметим, что $$72=2\cdot36$$
Сделаем замену $$36=t$$ для удобства
$$\frac{\sin^22t\cdot\sin^2t}{\cos^22t\cdot\cos^2t}$$
Рассматривать будем выражение
$$\frac{\sin2t\cdot\sin t}{\cos2t\cdot\cos t}$$ – так как его потом можно легко возвести в квадрат и получить нужный нам ответ
Тут воспользуемся формулой двойных углов и получим
$$\frac{2(1−cos^2t)}{2cos^2t−1}$$, дальше упрощать бессмысленно
Если мы найдем $$\cos36$$, то можно смело подставлять, если вы помните чему он равен, то это замечательно.
$$\cos36=\frac{1+\sqrt{5}}{4}$$
Давайте попробуем вывести это
Рассмотрим $$\cos(180−α)=−\cosα$$
Пусть $$α=2t$$
$$180=5t$$
$$\cos(5t−2t)=−\cos2t$$
$$\cos(5t−t)=\cos(180−36)=−\cos2t$$
$$\cos3t=−\cos2t$$
$$4\cos^3t−3cos^2t=sin^2t−cos^2t$$
Обозначим $$\cos t=x, 0<x<1$$
$$4x^3−3x=1−2x^2$$
$$4x^3−3x+2x^2−1=0$$
Делители $$\pm1$$, проверкой можно выяснить, что $$x=−1$$ – является корнем уравнения
Тогда делим столбиком на $$x+1$$
$$(x+1)(4x^2−2x−1)=0$$
$$x=−1$$ – не подходит
Решая квадратное уравнение, получаем
$$x=\frac{1+\sqrt{5}}{4}$$
(это не единственный способ)
$$\cos^236=\frac{1+2\sqrt{5}+5}{16}$$
Подставляем это в наше выражение
После всех сокращений можно получить ответ
$$\frac{5-\sqrt{5}}{\sqrt{5}-1}=\sqrt{5}$$
$$(\sqrt{5})^2=5$$
Задание 10
Необходимо рассчитать значение $$t,$$ при котором $$l(t)=l_0+1,8\cdot10^{-3}$$ метров. Воспользуемся законом изменения длины рельс от температуры и выразим температуру, получим:
$$l_0+1,8\cdot10^{-3}=l_0+l_0at$$
$$l_0at=3\cdot10^{-3}$$
$$t=\frac{1,8\cdot10^{-3}}{l_0a}$$
$$t=\frac{1,8\cdot10^{-3}}{15\cdot1,2\cdot10^{-5}}=\frac{1,8\cdot10^{-3}}{18\cdot10^{-5}}=10$$
Задание 11
Пусть $$x$$ л вылили из бака
Тогда осталось $$64−x$$ л в баке, концентрация спирта $$\frac{64−x}{64}$$
Затем выливают еще $$x$$ л, в баке остается $$64−x−x\cdot\frac{64−x}{64}$$ л спирта
Тогда из условия составляем уравнение
$$64−x−x\cdot\frac{64−x}{64}=49$$
Решая квадратное уравнение
$$x=8$$
$$x=120$$ – больше чем 64, такого быть не может
$$x\cdot\frac{64−x}{64}$$ л спирта вылили во второй раз, подставляя $$x=8$$, получаем $$7$$ л.
Задание 12
Найдем критические точки:
$$y'=0$$
$$−4\cos x\cdot\sin x=0$$
$$−\sin2x=0$$
$$x=\frac{πn}{2}$$
Очевидно, что наиб значение будет при $$x=2π,4π,..,$$ т.к. косинус будет равен 1.
$$y(2\pi)=\frac{1}{2}(1+4)=2,5$$
Задание 14
Задание 16
Задание 17
Задание 19
б) Могут ли эти числа образовывать арифметическую прогрессию, если сумма первого, третьего и седьмого из них равна 90, а сумма всех чисел равна 810?
в) Могут ли первые восемь из этих чисел образовывать геометрическую прогрессию с целым знаменателем, если сумма этих восьми чисел равна $$103\cdot994$$?