242 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 242 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №242 (alexlarin.com)
Решаем ЕГЭ 242 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №242 (alexlarin.com)
Задание 1
Железнодорожный билет для взрослого стоит 820 руб. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 20 школьников и 2 взрослых. Сколько рублей стоят билеты на всю группу?
Стоимость билета школьника:820*0,5=410 Общая стоимость: 20*410+2*820=9840.
Задание 2
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8‐го класса по обществознанию в 2007 году. Среди указанных стран первое место принадлежит Японии. Определите, какое место занимает Словения.
1е место - Япония 2е место- Великобритания 3е место - Венгрия 4е место - Словения
Задание 3
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах.
Воспользуемся формулой пика. Узлов внутри(зеленые точки): 18, на сторонах( синие): 16
$$S=18+\frac{16}{2}-1=25$$.
Задание 4
Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,6. Сколько выстрелов потребуется чтобы мишень была поражена с вероятностью не меньше, чем 0,97.
Если вероятность поражения не менее 0,97, то вероятность промаха менее 1-0,97=0,03.
Вероятность промаха n раз подряд $$(1-0,6)^{n} \Rightarrow$$$$0,4^{n}< 0,03\Rightarrow n=4.$$
Задание 5
Точки А и В делят окружность на две дуги, длины которых относятся как 7:8. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
Пусть AB-большая , AB' меньшая дуга, тогда AB+AB'=360 . Пусть AB=8x , тогда AB'=7x:
8x+7x=360 $$\Leftrightarrow$$ 15x=369 $$\Leftrightarrow x=24$$, тогда AB=192, AB'=168
Центральный угол равен величине дуги, на которую он опирается.
Задание 6
На рисунке изображен график функции y=f(x) и отмечены точки ‐7, ‐3, 1, 5. В какой из этих точек значение производной этой функции наибольшее? В ответе укажите эту точку
Если f(x) возрастает , то f'(x)> 0 , если f(x) убывает, то f'(x)< 0 . В точках -3; 1; 5 f'(x)> 0. При этом касательная в точке 5 имеет большой угол $$\Rightarrow f'_{max}=f'(5).$$
Задание 7
В сосуд, имеющий форму конуса, налили 20 мл жидкости до половины высоты сосуда. Сколько жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Пусть $$V_{1}$$- объем жидкости,$$V_{2}$$- объем сосуда.$$r_{1}; h_{1}$$- радиус и высота первого и $$r_{2}; h_{2}$$- второго
Из подобия $$\Delta ABC$$ и $$AB_{1}C_{1}$$:
$$\frac{AB}{AB_{1}}=\frac{1}{2}\Rightarrow$$$$r_{1}=\frac{1}{2}r_{2}$$
$$h_{1}=\frac{1}{2}h_{2}$$
$$V_{1}=\frac{1}{3}\pi r_{1}^{2}h_{1}=$$$$\frac{1}{3}\pi (\frac{1}{2}r_{2})^{2}*\frac{1}{2}*h_{2}=$$$$\frac{1}{8}*\frac{1}{3}\pi r_{2}^{2}h_{2}=\frac{1}{8}V_{2}.$$
Следовательно, $$V_{2}=8V_{1}=160$$, а долить надо 160-20=140.
Задание 8
Найдите значение выражения $$\frac{b^{2}\sqrt[6]b}{\sqrt[10]b*\sqrt[15]b}$$, при b=6
$$\frac{b^{2}*\sqrt[6]{b}}{\sqrt[10]{b}*\sqrt[15]{b}}=$$$$\frac{b^{2}*b^{\frac{1}{6}}}{b^{\frac{1}{10}}*b^{\frac{1}{15}}}=$$$$b^{2+\frac{1}{6}-\frac{1}{10}-\frac{1}{15}}=b^{2}=6^{2}=36$$
Задание 9
По закону Ома для полной цепи сила тока равна $$I=\frac{\varepsilon}{R+r}$$ , где $$\varepsilon=12$$В ‐ ЭДС источника, r=1 Ом – его внутреннее сопротивление, R ‐ сопротивление цепи. При каком наименьшем сопротивлении цепи сила тока будет составлять не более 10% силы тока короткого замыкания $$I_{K3}=\frac{\varepsilon}{r}$$ ? Ответ дайте в Омах
$$I\leq 0,1I_{k3}\Rightarrow \frac{\varepsilon }{R+r}\leq \frac{1}{10}*\frac{\varepsilon }{r}\Leftrightarrow$$$$\frac{1}{R+r}\leq \frac{1}{10r}\Leftrightarrow $$$$R+r\geq 10r\Leftrightarrow R\geq 9r\Leftrightarrow R\geq 9$$.
Следовательно, минимальное значение составит 9 Ом
Задание 10
Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть x кг-масса первого, тогда никеля в нем 0,1x кг. Пусть y кг –масса второго, тогда 0,3y кг-масса никеля в нем. Получили сплав 200 кг(x+y=200) и никеля в нем 0,25*200(0,1x+0,3y=50) $$\left\{\begin{matrix}x+y=200\\0,1x+0,3y=50|*10 \end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}x+y=200\\x+3y=500\end{matrix}\right.$$ Вычтем из 2-го уравнения 1-го: $$x+3y=(x-y)=500-200$$ $$2y=300$$ $$y=150$$ Тогда масса 1-го: 200=150=50кг. Разница масс :150-50=100 кг.
Задание 11
Найдите точку минимума функции $$y=(2x-3)\cos x -1-2\sin x +10$$ принадлежащую промежутку $$(0; \frac{\pi}{2})$$
$$y=(2x-3)\cos x-2\sin x+10$$
Найдем производную заданной функции:
$$y'=(2x-3)'\cos x+(2x-3)(\cos x)'-2(\sin x)'=2\cos x-\sin x(2x-3)-2\cos x=0$$
Приравняем производную к нулю:
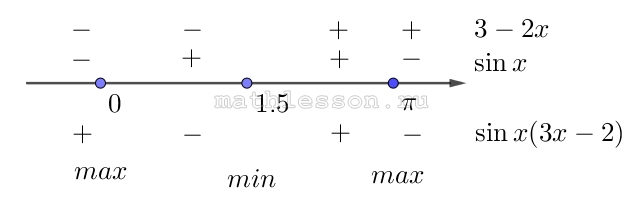
$$\sin x(3-2x)=0$$
Найдем точки экстремума:
$$\left[\begin{matrix}\sin x=0\\3-2x=0\end{matrix}\right.\Leftrightarrow$$$$ \left[\begin{matrix}x=\pi *n, n\in Z \\x=+1,5\end{matrix}\right.$$
Рассмотрим какие значения принимает производная на полученных промежутках:
Как видим, точка минимума соответсвует 1,5
Задание 12
а) $$\frac{4 \cos x-5}{2 \cos x -1}+\frac{1}{2 cos^{2}x-\cos x}=2|*(2 \cos^{2} x-\cos x)$$
Найдем ограничение по y:
$$\left\{\begin{matrix}2 \cos x-1\neq 0 \\2 \cos^{2} x-\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}\cos \neq \frac{1}{2} \\\cos x(2 \cos x-1)\neq 0\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}\cos x\neq \frac{1}{2}\\\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x\neq \pm \frac{\pi }{3}+2\pi n\\x\neq \frac{\pi }{2}+\pi n,n\in Z\end{matrix}\right.$$
$$(4 \cos x-5) \cos x+1=2(2 \cos^{2 }x -\cos x)$$
$$4 \cos^{2}x -5 \cos x+1-4 \cos^{2}x+2 \cos x=0$$
$$-3 \cos x+1=0$$
$$\cos x=\frac{1}{3}\Leftrightarrow$$$$x\pm \arccos\frac{1}{3}+2\pi n, n\in Z$$
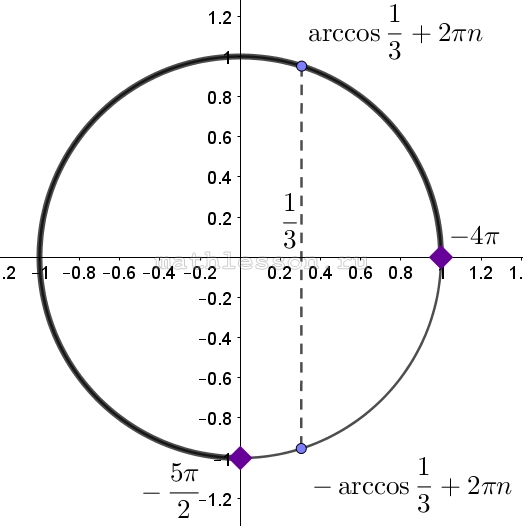
б) Отметим полученные корни, заданный промежуток на единичной окружности:
Как видим один корень попадает в заданный промежуток. Найдем его частный случай: $$-4\pi+\arccos \frac{1}{3}$$
Задание 13
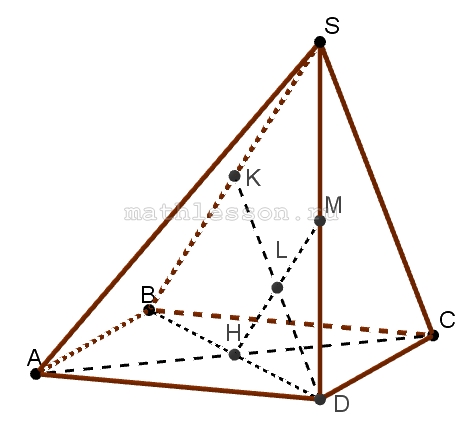
В основании пирамиды SABCD лежит квадрат ABCD со стороной 8. Боковое ребро SD перпендикулярно плоскости основания. Точка М‐середина высоты пирамиды. Плоскость ACM составляет угол 45 с плоскостью основания.
$$\angle MHD=45;SD\perp (ABC)$$
a)$$1)SD\perp (ABC)\Rightarrow SD$$-высота, тогда SM=MD.
2)ABCD-квадрат $$\Rightarrow AC\perp BD$$.
Пусть $$AC\cap BD=H$$,тогда $$DH\perp AC\Rightarrow MH\perp AC$$( по теореме о 3х перпендикулярах), тогда $$\angle MHD=45$$.
3)DH=HB(свойство диагоналей квдрата), тогда $$\Delta MHD\sim \Delta BSD\Rightarrow MH || SB\Rightarrow SB\left | \right |(AMC)$$.
б) 1)т.к. $$SB\left | \right | (AMC)$$,то d-расстояние от B до (AMC) равно расстоянию от SB до MH.
2) Опустим $$DK\perp SB, DK\cap MH=L\Rightarrow d=KL=\frac{1}{2}DK$$
3)из $$\Delta ABD: BD=\sqrt{8^{2}+8^{2}}=8\sqrt{2}$$.
4) $$\angle MHD=45\Rightarrow \Delta MHD$$ и $$\Delta BSD$$-равнобедренный $$\Rightarrow KD=BD*\sin B=8\sqrt{2}*\frac{\sqrt{2}}{2}=8$$.
5) $$KL=\frac{1}{2}KD=4.$$
Задание 14
Решите неравенство $$\log_{\frac{1}{3}} \frac{x-4}{x+4}-\log_{\frac{x+4}{x-4}} 3> 0$$
$$log_{\frac{1}{3}}\frac{x-4}{x+4}-log_{\frac{x+4}{x-4}}3> 0$$
ОДЗ:
$$\left\{\begin{matrix}\frac{x-4}{x+4} > 0& & \\\frac{x-4}{x+4}\neq 1 & &\end{matrix}\right.x\in (-\infty ;-4)\cup (4; +\infty )$$
$$log_{3}\frac{x+4}{x-4}-\frac{1}{log_{3}\frac{x+4}{x-4}}> 0$$
Введем замену:
$$log_{3}\frac{x+4}{x-4}=a$$
Получим:
$$a-\frac{1}{a}> 0\Rightarrow \frac{a^{2}-1}{a}> 0$$
$$\left[\begin{matrix}\left\{\begin{matrix}a>-1\\ a<0\end{matrix}\right.\\ a>1\end{matrix}\right.$$
Тогда:
$$\left[\begin{matrix}\left\{\begin{matrix}\log_{3} \frac{x+4}{x-4}>-1\\ log_{3}\frac{x+4}{x-4}<0\end{matrix}\right.\\ log_{3}\frac{x+4}{x-4}>1\end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}\left\{\begin{matrix}\frac{x+4}{x-4}>\frac{1}{3}\\ \frac{x+4}{x-4}<1\end{matrix}\right.\\ \frac{x+4}{x-4}>3\end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}\left\{\begin{matrix}\frac{2x+16}{x-4}>0\\ \frac{8}{x-4}<0\end{matrix}\right.\\ \frac{-2x+16}{x-4}>0\end{matrix}\right.$$
Отметим решение внутренней системы (первые два неравенства):
Отметим решение третьего неравенства:
Отметим решение всей совокупности:
С учетом ОДЗ видим, что конечное решение будет: $$(-\infty ; -8)\cup (4;8)$$
Задание 15
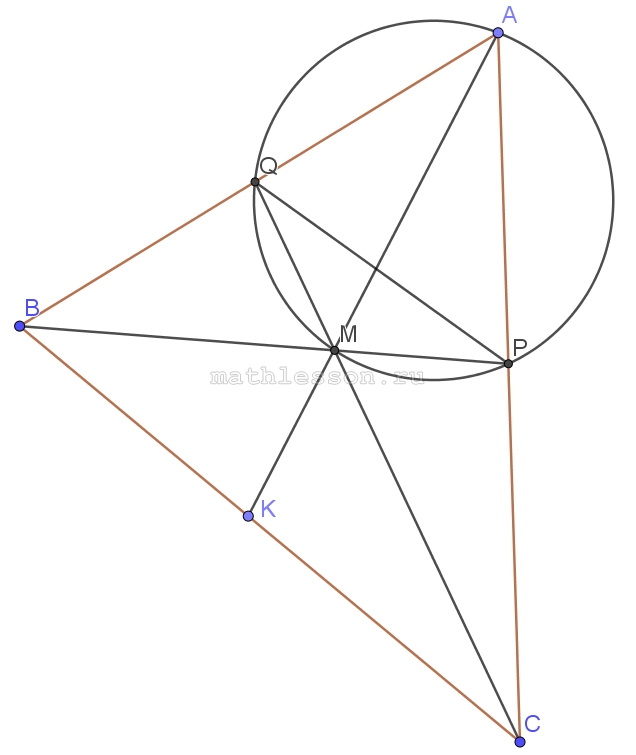
Точка M пересечения медиан треугольника ABC , вершина A и середины сторон AB и AC лежат на одной окружности.
a)1) Пусть $$CM\cap AB=Q; BM\cap AC=P$$, тогда QP-средняя линия $$\Rightarrow QP\left | \right |BC\Rightarrow \Delta QPM\sim \Delta BMC \angle BPQ=\angle PBC$$
2) $$\angle QPM=\angle QAM$$(вписанные и опираются на одну дугу)$$\Rightarrow \angle QAM=\angle MBK \angle BKA$$-общий $$\Rightarrow \Delta ABK\sim \Delta MBK$$.
b)1)Пусть MK=x,тогда по свойству имеем MA=2x.Из подобия $$\Delta ABK$$ и $$\Delta MBK$$
$$\frac{BK}{KM}=\frac{AK}{BK}\Rightarrow BK^{2}=AK*KM.$$
2)$$BK=\frac{1}{2}BC=3\sqrt{3}$$,тогда $$(3\sqrt{3})^{2}=3x*x\Rightarrow$$ x=3,тогда AK=9.
Задание 16
Фирма имеет возможность рекламировать свою продукцию, используя местные радио и телевизионную сети. Затраты на рекламу в бюджете фирмы ограничены величиной 1000$ в месяц. Каждая минута радиорекламы обходится в 5$, а каждая минута телерекламы ‐ в 100$. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения, но при этом фирма решила, что время радиорекламы не должно превышать двух часов. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определите оптимальное распределение финансовых средств, ежемесячно отпускаемых на рекламу, между радио‐ и телерекламой, если время можно покупать только поминутно.
Пусть x-эффективность радио 1 минуты ,тогда 25x-1 минуты теле При этом цена теле в $$\frac{100}{5}=20$$ раз выше. Получаем, что прирост эффективности к цене от радио к теле составит $$\frac{25}{20}$$ т.е. эффективность растет быстрее цены. Тогда $$t_{1}$$-время теле берем максимум $$\frac{1000}{100}=10$$ мин. , но 1 взять не можем, т.к. $$t_{2}$$-время радио должно быть в 2 раза больше. Т.к. $$t_{1}$$ и $$t_{2}\in N$$, возьмем $$t_{1}=9$$,тогда бюджет для $$t_{2:}1000-9*100=100$$. Тогда $$t_{2}=\frac{100}{5}=20$$. Все условия выполнены. Следовательно под радио отдадим 20*5=100$, а под теле 900$
Задание 17
При каких значениях параметра a система $$\left\{\begin{matrix}y=2ax-2x^{2}+6a-4\\ y=\frac{3*3^{x^{2}}}{27^{a}}-\frac{3^{ax}}{3}\end{matrix}\right.$$ имеет не менее двух решений?
$$\left\{\begin{matrix}y=2ax-2x^{2}+60-4 & & \\y=\frac{3*3^{x^{2}}}{27^{a}}-\frac{3^{ax}}{3}& &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}y_{1}=2(-x^{2}+ax+3a-2) & & \\y_{2}=3^{x^{2}-3a+1}-3^{2x-1} & &\end{matrix}\right.$$
Рассмотрим монотонность $$y_{2}$$:
$$3^{x^{2}-3a+1}-3^{ax-1}>0$$
$$3^{x^{2}-3a+1}>3^{ax-1}$$
$$x^{2}-3a+2>0$$
$$x^{2}-ax-3a+2>0$$
Пусть $$x^{2}-ax-3a+2=f$$. Тогда $$y_{1}=-2f$$. Получаем, если $$f>0$$,то $$y_{2}>0$$, но $$y_{1}<0$$ ,и наоборот . Тогда $$y_{1}=y_{2}$$ только при условии , что $$f=0$$.
$$x^{2}-ax-3a+2=0$$
$$D=a^{2}-4(2-3a)=a^{2}+12a-8>0$$
$$D=144+32=176$$
$$a_{1,2}=\frac{-12\pm \sqrt{176}}{2}=-6\pm \sqrt{44}=-6\pm 11$$, тогда
$$a\in (-\infty; -6;-\sqrt{11})\cup (-6; +\sqrt{11};+\infty )$$
Задание 18
В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2046.
a) По формуле арифм. прогрессии : $$a_{n}=\frac{a_{n-1}+a_{n+1}}{2}$$, тогда $$a_{2}=\frac{1+2046}{2}\notin N$$. Значит это не арифм. прогрессия. По формуле геоиетр. прогрессии: $$b_{n}=\sqrt{b_{n-1}*b_{n+1}}$$, тогда $$b_{2}=\sqrt{1*2046}\notin N$$. Значит это не геометр. прогрессия. б) $$a_{4}=a_{1}+d(4-1)=1+3d=2046$$ $$3d=2046\Rightarrow d\notin N$$ $$b_{4}=b_{1}*q^{4-1}=1*q^{3}=2046$$ $$q=\sqrt[3]{2046}\notin N$$ Так же необходимо рассмотреть случаи, когда первые три члена - арифметическая, а последние три - геометрическая прогрессии и наоборот. 1) Если сначала арифметическая, то имеем первые три члена: $$1, 1+d, 1+2d$$, тогда последние три: $$1+d, (1+d)q, (1+d)q^{2}$$(начали со второго умножать на q). Тогда получаем, что третий член выражается как $$1+2d$$ и $$(1+d)q$$, то есть $$1+2d=(1+d)q$$. Отсюда $$d=\frac{1-q}{q-2}=-1+\frac{-1}{q-2}$$. С учетом натуральности q и d, решений нет. Значит такая ситуация не подходит 2) Сначала геометрическая. Аналогично рассуждая, получим первые три члена: $$1, q, q^{2}$$, тогда последние три: $$q, q+d, q+2d$$. Тогда рассмотрим третий член: $$q^{2}=q+d$$. Данное уравнение не имеет решения в натуральный q и d. Значит, не подходит такая ситуация. в) Пусть дана арифм. прогрессия. $$a_{n}=a_{1}+d(n-1)=2046$$ $$1+d(n-1)=2046\Leftrightarrow d(n-1)=2046=1*5*409.$$ Т.е. $$d=409, n-1=5\Rightarrow n=6$$. Т.е. 6 членов, разность равна 409.