316 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
Задание 2
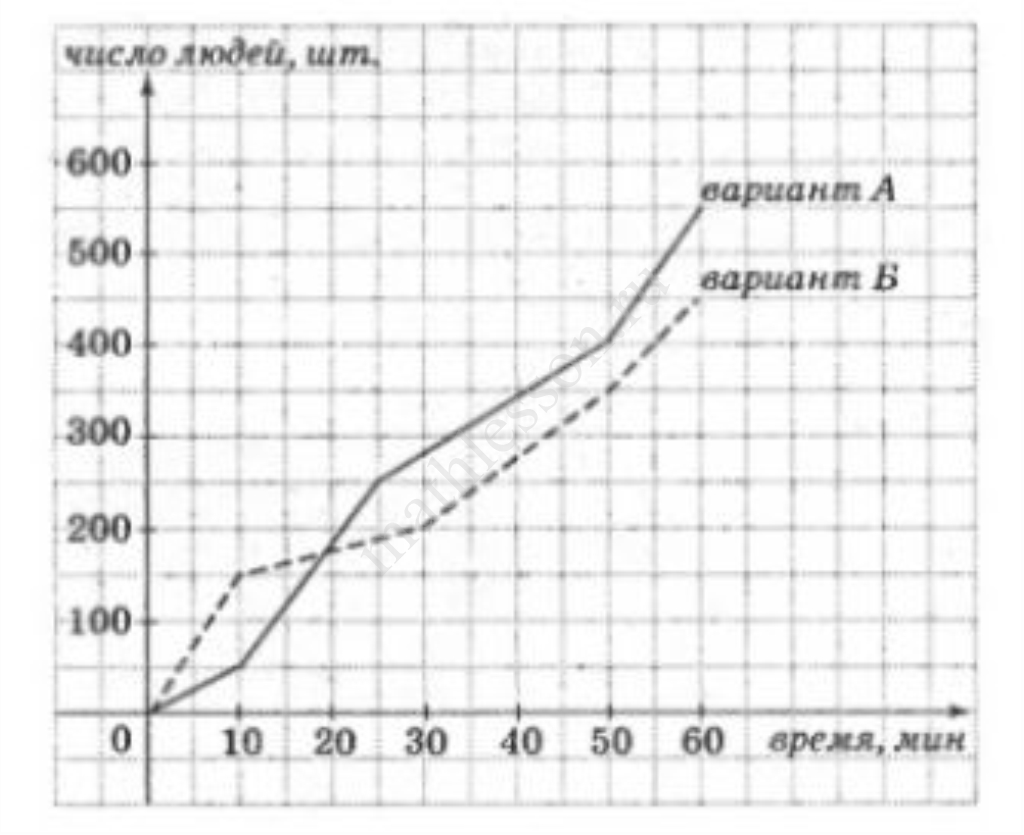
На улицах города в течение часа проводился социологический опрос, в ходе которого каждый из опрашиваемых должен был выбрать один из вариантов ответа: вариант А или вариант Б. На графиках показаны результаты этого опроса. (По горизонтальной оси откладывается время, прошедшее с начала опроса – в минутах, а по вертикальной – количество людей, выбравших за это время соответствующий вариант ответа). Какая часть людей от общего числа всех опрошенных проголосовала за последние 10 минут проведения этого опроса?
Задание 10
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объем и давление связаны соотношением $$pV^{1,4}=const$$, где $$p$$ ‐ давление газа (в атмосферах), $$V$$ ‐ объем газа (в литрах). Изначально объем газа равен 294,4 л, а давление газа равно одной атмосфере. До какого объема надо сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Задание 14
В правильной треугольной пирамиде SABC сторона основания АВ равна 6, а боковое ребро SA равно 4. Точки М и N – середины ребер SA и SB соответственно. Плоскость $$\alpha$$ содержит прямую MN и перпендикулярна плоскости основания пирамиды.
Задание 16
Точки А и В лежат на окружности с центром О и радиусом 6, а точка С равноудалена от точек А, В и О. Другая окружность с центром Q и радиусом 8 описана около треугольника АСО.
Задание 17
15 декабря планируется взять кредит в банке на 61 месяц. Условия его возврата таковы:
Задание 19
Натуральное число, являющееся полным квадратом, обладает следующим свойством: если все его цифры уменьшить на одно и то же натуральное число, то получится число, также являющееся полным квадратом.