399 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
Задание 1
Пусть гипотенуза x
$$BK_1=BK_2=\frac{5}{17}x$$
$$BC=\frac{5}{17}x+6$$
$$AK_1=AK_3=\frac{12}{17}x$$
$$AC=\frac{12}{17}x+6$$
$$r=\frac{S}{p}\Rightarrow 6=\frac{(6+\frac{12}{17}x)(6+\frac{5}{17}x)}{2x+12}$$
$$10x^2-289x-6\cdot289=0$$
$$x>0$$
$$\frac{289\pm\sqrt{289^2+240\cdot289}}{20}$$
$$\frac{289\pm\sqrt{289\cdot529}}{20}$$
$$x=\frac{289+17\cdot23}{20}=34$$
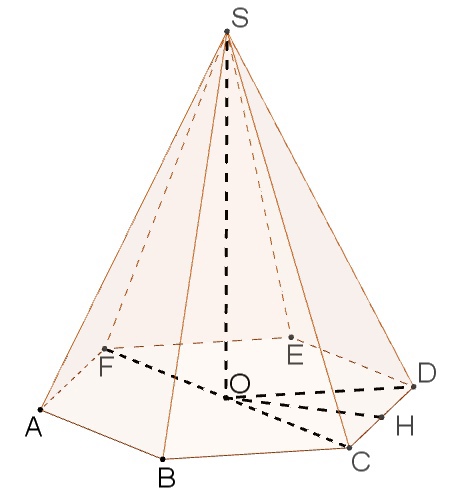
Задание 2
Пусть $$SO$$ - высота пирамиды; $$SH$$ - высота боковой грани $$SDC.$$ Тогда $$OH\perp CD$$ по теореме о трёх перпендикулярах.
$$\tg SHO=2\Rightarrow\cos SHO=\sqrt{\frac{1}{1+4}}=\frac{1}{\sqrt{5}}$$
Пусть $$CD=x\Rightarrow$$ из $$\Delta COD$$: $$OH=x\cdot\frac{\sqrt{3}}{2}$$
Тогда $$SH=x\cdot\frac{\sqrt{3}}{2}:\frac{1}{\sqrt{5}}=\frac{\sqrt{15}x}{2}$$
Из $$\Delta SHD$$: $$(\frac{\sqrt{15}x}{2})^2+(\frac{x}{2})^2=8^\Rightarrow\frac{16x^2}{4}=8^2\Rightarrow(2x)^2=8^2\Rightarrow2x=8\Rightarrow x=4$$
Задание 3
Вероятность события - это отношение количества "благоприятных" исходов ко всем возможным исходам.
Давайте посчитаем все возможные исходы:
Всего монет: $$10+11+12 = 33.$$ Вытаскиваем $$2$$ монеты из $$33.$$ Это можно сделать $$(33\cdot32)$$ способами
Теперь посчитаем "благоприятные" события. Для этого давайте поймем, какие варианты нас устраивают: $$1+1$$ - не устраивает; $$1+2 = 2+1$$ - не устраивает; $$2+2$$ - не устраивает;
$$1+5 = 5+1$$ - устраивает; $$2+5 = 5+2$$ - устраивает; $$5+5$$ - устраивает
Посчитаем количество каждого "благоприятного" варианта.
1 и 5: $$10\cdot12 = 120$$ (10 однорублевых на 1 месте и для каждого 12 пятирублевых на втором)
5 и 1: $$12\cdot10 = 120$$ (тут наоборот 12 пятирублевых на первом и 10 однорублевых на втором)
2 и 5: $$11\cdot12 = 132$$ (тут аналогично)
5 и 2: $$12\cdot11 = 132$$ (тут анадогично)
5 и 5: $$12\cdot11 = 132$$ (12 пятирублевых на 1 место и осталось 11 пятирублевых для второго)
Итого: $$120+120+132+132+132 = 636$$
Таким образом вероятность:
$$P = \frac{636}{33\cdot32} = \frac{212}{11\cdot32} = \frac{53}{88}\approx 0,602$$
Задание 4
Тут задача на условную вероятность.
Если бы в задаче не было оговорки про попадание 2 пуль. А просто посчитать из всех возможных вариантов. То тогда, раз события независимы (попадание каждого), то итоговая вероятность считается умножением вероятностей событий. То есть событие: (первый не попал; второй попал; третий попал) = $$P(не1)\cdot P(2)\cdot P(3) = 0,3\cdot0,75\cdot0,8 = 0,18$$
Но в задаче вводят дополнительное условие: "известно, что попали ровно 2 пули".
А это меняет условие: Надо посчитать вероятность, при условии, что попали 2 пули.
По определению: Вероятность События A при условии события B равна отношению вероятности (пересечения A и B) ко всем возможным событиям B.
По простому: Надо посчитать все возможные вероятности, когда попали ровно 2 раза - это знаменатель. И из них выбрать вероятность, когда попали только 2-й и 3-й
Считаем: попали ровно 2 раза
$$P(B) = P(1)\cdot P(2)\cdot P(не3) + P(1)\cdot P(3)\cdot P(не2) + P(2)\cdot P(3)\cdot P(не1)$$
$$P(B) = 0,7\cdot0,75\cdot0,2 + 0,7\cdot0,8\cdot0,25 + 0,75\cdot0,8\cdot0,3$$
$$= 0,105 + 0,14 + 0,18 = 0,425$$
А вероятность $$P(A\cap B)$$ - это пересечение, что 2 и3 попали и попало только двое (значит первый не попал) - это уже посчитано $$= 0,3\cdot0,75\cdot0,8 = 0,18$$
Таким образом требуемая условная вероятность
$$P(\frac{A}{B}) = \frac{P(A\cap B)}{P(B)}$$
$$P(\frac{A}{B}) = \frac{0,18}{0,425}\approx 0,42$$
Задание 5
$$\frac{28^x}{14^6}=7^{5x-2}\cdot2^{6x-2}\Leftrightarrow\frac{(7\cdot2^2)^x}{(7\cdot2)^6}=7^{5x-2}\cdot2^{6x-2}\Leftrightarrow7^{x-6}\cdot2^{2x-6}=7^{5x-2}\cdot2^{6x-2}\Leftrightarrow$$
$$\Leftrightarrow\frac{7^{x-6}}{7^{5x-2}}=\frac{2^{6x-2}}{2^{2x-6}}\Leftrightarrow7^{-4x-4}=2^{4x+4}\Leftrightarrow(\frac{1}{7})^{4x+4}=2^{4x+4}\Rightarrow4x+4=0\Rightarrow x=-1$$
Задание 6
$$\frac{5\sin a-6\cos a}{6\sin a-10\cos a}=\frac{\sin a}{\cos a}\Leftrightarrow5\sin a\cos a-6\cos^2 a=6\sin^2 a-10\sin a\cos a\Rightarrow$$
$$\Rightarrow15\sin a\cos a=6\sin^2 a+6\cos^2 a\Rightarrow7,5\sin2a=6\Rightarrow\sin2a=\frac{4}{5}=0,8$$
Задание 7

Задание 8
$$v=\sqrt{2la}$$
$$v^2=2la$$
$$l=\frac{v^2}{2a}=\frac{60^2}{2\cdot3600}=\frac{3600}{2\cdot3600}=0,5$$ км
Задание 9
Примем среднюю стоимость гостиничного номера в феврале месяце равной 1.
Соответственно среднюю стоимость гостиничного номера в августе месяце мы можем представить в виде:
$$1 + 1\cdot\frac{60}{100} = 1,6.$$
Обозначим через переменную $$k$$ количество процентов, на которое необходимо будет понизить стоимость гостиничного номера в течении осени.
Запишем уравнение и рассчитаем чему должно равняться $$k,$$ чтобы были выполнены условия:
$$1,6 - 1,6\cdot\frac{k}{100} = 1 + \frac{8}{100}$$
$$k = \frac{-0,52}{-1,6}\cdot100$$
$$k = 32,5$$
Задание 11
Найдем критические точки $$y′=0$$
$$3\pi\cdot\cos x−\frac{3x-\pi}{\pi}\cdot\sin x−\frac{3}{\pi}\cos x=0$$
$$-\frac{3x-\pi}{\pi}\cdot\sin x=0$$
$$\sin x=0$$ $$x=\pi n$$
$$x=\frac{\pi}{3}$$
Так как отрезок $$[0;2\pi],$$ то подозрительные точки:
$$x=0,\frac{\pi}{3},\pi,2\pi$$
Проверяем все
$$y(2\pi)=26$$
Задание 12
Задание 13
Задание 15
1. Если объём заказа не превышает 4000 единиц товара, то выручка фирмы не превышает $$4000\cdot300=1200000$$ руб.
2. Если объём заказа $$4000< x\leq 16000,$$ где x — количество единиц товара в заказе, то выручка S (в руб.) равна
$$S(x)=(300-\frac{x-4000}{50})\cdot x=\frac{1}{50}(19000-x)x.$$
Найдём, при каком значении x выражение S(x) принимает наибольшее значение.
Если раскрыть скобки, то S(x) окажется квадратичной функцией с отрицательным старшим коэффициентом. Она принимает своё наибольшее значение в точке $$x_0=\frac{x_1+x_2}{2}:$$
$$x_0=\frac{19 000-0}{2}=9500.$$
Найденное число удовлетворяет требуемому объёму заказа. Найдём $$S(x_0):$$
$$S(x_0)=\frac{1}{50}(19000-9500)\cdot9500=190\cdot9500=1 805 000$$ (руб.).
Найденная сумма превышает максимальную выручку при $$0< x\leq 4000,$$ значит, наибольшую выручку фирма получит при объёме заказа в 9500 единиц товара.