359 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
Пусть $$4^x=t$$, $$t>0$$
$$t−\frac{16}{t}−15=0$$ умножаем всё на $$t>0$$
$$t^2−15t−16=0$$
$$t=−1$$
$$t=16$$
Из ограничений $$t>0$$
$$t=16$$
$$4^x=16$$
$$x=2$$
Задание 2
Событие $$A$$ – кофе закончится в первом автомате
Событие $$B$$ – кофе закончится во втором автомате
События $$A$$ и $$B$$ – совместные
По условию:
$$P(A)=0,3$$
$$P(B)=0,3$$
$$P(AB)=0,12$$
Найдем противоположную искомой вероятность (кофе закончится хотя бы в одном автомате)
$$P(A+B)=P(A)+P(B)−P(AB)=0,3+0,3−0,12=0,48$$
Искомая вероятность $$1-0,48=0,52$$
Задание 4
Подставим сразу $$x=2$$ для удобства:
$$\sqrt{9-4\sqrt{5}}+\sqrt{14-6\sqrt{5}}=\sqrt{4-4\sqrt{5}+5}+\sqrt{9-6\sqrt{5}+5}=$$
$$=\sqrt{(2-\sqrt{5})^2}+\sqrt{(3-\sqrt{5})^2}=|2-\sqrt{5}|+|3-\sqrt{5}|=$$
$$=\sqrt{5}-2+3-\sqrt{5}=1$$
Задание 5
$$V_0=S_{осн}\cdot h=S_{осн}\cdot12=2000$$
Откуда $$S_{осн}=\frac{500}{3}$$
После погружения детали
$$V_1=S_{осн}\cdot21=?$$
Площадь основания не изменилась
$$V_1=\frac{500}{3}\cdot21=3500$$
$$V_{иск}=V_0−V_1=1500$$
Задание 7
$$1,4+14t−5t^2\geq8$$
$$t\in [\frac{3}{5};\frac{11}{5}]$$
Значит, время в течении которого мяч будет находится на высоте не менее 8 метров
$$t_{иск}=\frac{11}{5}−\frac{3}{5}=1,6$$
Задание 8
$$V_1=65,V_2=60$$
$$S_1=65\cdot\frac{24}{60}=26$$
$$S_2=60\cdot\frac{24}{60}=24$$
Значит, время за которое третий автомобиль догнал первый: $$t_1=\frac{S_1}{V_3−65}$$
Время за которое третий автомобиль догнал второй: $$t_2=\frac{S_1}{V_3−60}$$
По условию
$$t_1−t_2=\frac{40}{60}$$
$$\frac{26}{V_3−65}−\frac{24}{V_3−60}=\frac{2}{3}$$
Откуда легко найти $$V_3$$
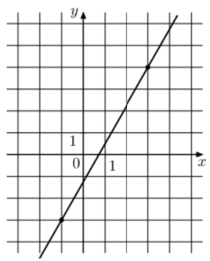
Задание 9
Найдем $$k$$ и $$b$$, на рисунке уже выделены две точки, которые можно подставить в функцию и найти неизвестные
$$\left\{\begin{matrix} 4=3k+b\\ -3=-k+b \end{matrix}\right.$$
Решаем систему.
$$f(x)=\frac{7}{4}x−\frac{5}{4}$$
$$f(−5)=−10$$
Задание 10
Первые два фломастера, которые мы вытащим, должны быть красные
$$P_{иск}=\frac{4}{6}\cdot\frac{3}{5}\cdot\frac{2}{4}=0,2$$
Задание 11
Перепишем функцию
$$y=x−6+\frac{36}{x}$$
$$y'=1−\frac{36}{x^2}$$
Найдем подозрительные точки:
$$y'=0$$
$$x=−6$$ – не входит в отрезок
$$x=6$$
По методу интервалов $$x=-6$$ – max, $$x=6$$ – min
$$y(6)=6-6+6=6$$
Задание 13
Задание 15
| Начало года | 2022 | 2023 | 2024 | 2025 | 2026 |
| Долг (в млн. рублей) | S | 0,8S | 0,5S | 0,3S | 0 |