263 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 263 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №263 (alexlarin.com)
Решаем ЕГЭ 263 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №263 (alexlarin.com)
Задание 1
Три чижа и два ужа весят 116 г. Два чижа и три ужа весят 144 г. Сколько граммов весит один уж?
Пусть x гр. –масса одного чижа, y - одного ужа, тогда: $$\left\{\begin{matrix}3x+2y=116 |*2\\2x+3y=144|*3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}6x+4y=232\\6x+9y=432\end{matrix}\right.$$
Вычтем из 2 уравнения 1: $$5y=200\Leftrightarrow$$ $$y=40$$
Задание 2
На рисунке жирными точками показана среднесуточная температура воздуха в Вене каждый день с 6 по 19 июня 1919 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, сколько дней из указанного периода среднесуточная температура не превышала 180 C .
Задание 3
По т. Пифагора : $$AC=\sqrt{AD_{1}^{2}+CD_{1}^{2}}=$$$$\sqrt{12^{2}+5^{2}}=13$$
Задание 4
У биатлониста Антона вероятность попадания в мишень при каждом выстреле одинакова. Вероятность, что при двух выстрелах Антон оба раза промахнется, равна 0,04. Какова вероятность, что при двух выстрелах Антон поразит ровно одну мишень?
Пусть x – вероятность одного промаха, тогда двух подряд: $$x^{2}=0,04\Leftrightarrow$$ $$x=0,2$$. Тогда вероятность попадания $$1-0,2=0,8$$. Одну мишень он поразит или $$0,8*0,2$$ (попал, не попал), или $$0,2*0,8$$ (не попал, попал). Тогда итоговая вероятность одного попадания и промаха: $$P=0,16+0,16=0,32$$
Задание 5
Найдите корень уравнения $$\log_{0,5} (x+5)=\log_{2} (x+5)$$
$$\log_{0,5}(x+5)=\log_{2}(x+5)\Leftrightarrow$$ $$\log_{2^{-1}}(x+5)=\log_{2}(x+5)\Leftrightarrow$$ $$(-1)\log_{2}(x+5)=\log_{2}(x+5)\Leftrightarrow$$ $$2\log_{2}(x+5)=0\Leftrightarrow$$ $$x+5=1\Leftrightarrow$$ $$x=-4$$
Задание 6
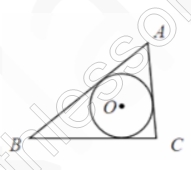
Точка О – центр окружности, вписанной в треугольник АВС. Найдите сумму углов ОАВ, ОВС и ОСА. Ответ дайте в градусах.
Центр вписанной окружности лежит в точке пересечения биссектрис $$\Rightarrow$$ $$\angle OAB =0,5 \angle A$$; $$\angle OBC=0,5 \angle B$$; $$\angle OCA=0,5 \angle C$$; Тогда: $$\frac{\angle A+\angle B+\angle C}{2}=\frac{180}{2}=90$$
Задание 7
Используя геометрический смысл определенного интеграла, вычислите $$\int_{-2}^{0}\frac{1}{\pi}\sqrt{4-x^{2}}dx$$
Рассмотрим функцию $$y=\sqrt{4-x^{2}}$$ - это полуокружность радиуса 2 с центром в начале координат . При этом по $$x \in [-2; 0]$$ получим четверть данной окружности : $$S=\frac{1}{4} \pi 2^{2}=\pi$$ . Геометрический смысл интеграла в нахождении площади криволинейного трапеции, тогда: $$\int_{-2}^{0} \frac{1 }{\pi }\sqrt{4-x^{2}}dx=$$$$\frac{1}{\pi}*\int_{-2}^{0}\sqrt{4-x^{2}}dx=$$$$\frac{1}{\pi}*\pi=1$$
Задание 8
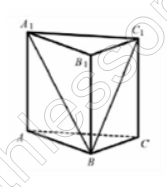
Дана правильная треугольная призма ABCA1B1C1, площадь основания которой равна 12, а боковое ребро равно 6. Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, C1.
- Найдем $$V_{A_{1}B_{1}C_{1}B}=$$$$\frac{1}{3}S_{A_{1}B_{1}C_{1}}*BB_{1}=$$$$\frac{1}{3}*12*6=24$$
- Найдем $$V_{ABCA_{1}B_{1}C_{1}}=12*6=72$$
- $$V_{ABCDA_{1}B_{1}}=$$$$V_{ABCA_{1}B_{1}C_{1}}-V_{A_{1}B_{1}C_{1}B}=$$$$72-24=48$$
Задание 9
Найдите значение выражения $$tg 199^{\circ}\cdot tg 289^{\circ}$$
$$tg 199*tg 289=$$$$tg(180+19)*tg(270+19)=$$$$tg 19 *(-ctg 19)=-1$$
Задание 10
Емкость высоковольтного конденсатора в телевизоре С = 4∙10‐6 Ф. Параллельно с конденсатором подключен резистор с сопротивлением R = 4∙106 Ом. Во время работы телевизора напряжение на конденсаторе U0 = 54 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением $$t=\alpha RC\log_{3} \frac{U_{0}}{U}$$ (с), где α = 0,9 – некоторая константа. Определите наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 28,8 с. Ответ дайте в кВ (киловольтах).
Подставим данные значения в формулу: $$28,8=0,9*4*10^{6}*4*10^{-6}\log_{3}\frac{54}{u}\Leftrightarrow$$ $$\log_{3}\frac{54}{u}=\frac{28,8}{0,9* 4^{2}}=2\Leftrightarrow$$ $$\frac{54}{u}=3^{2}=9\Rightarrow$$ $$u=\frac{54}{9}=6$$
Задание 11
Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 120 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Пусть x км\ч –скорость второго. Тогда время в часах , за которое первый опережает второго на S км. :$$ t=\frac{S}{120-x}$$, следовательно, $$\frac{10}{120-x}=\frac{20}{60}\Leftrightarrow$$ $$\frac{10}{120-x}=\frac{10}{30}\Leftrightarrow$$ $$120-x=30\Leftrightarrow$$ $$x=90$$
Задание 12
Найдите наибольшее значение функции $$f(x)=(x^{2}-4)e^{x}$$ на отрезке [0;2]
Найдем производную данной функции и приравняем к 0: $${f}'(x)={(x^{2}-4)}'e^{x}+{(e^{x})}'(x^{2}-4)=0\Leftrightarrow$$ $$2xe^{x}+e^{x}(x^{2}-4)=0\Leftrightarrow$$ $$e^{x}(x^{2}+2x-4)=0\Leftrightarrow$$ $$D=4+16=20$$; $$x_{1,2}=\frac{-2 \pm \sqrt{20}}{2}=-1 \pm \sqrt{5}$$
на отрезке [0; 2] есть точка минимума ($$x=-1+\sqrt{5}$$), следовательно, наибольшее значение функция принимает в одном из концов:
Задание 13
Дано уравнение $$4^{\cos^{2} (x+\frac{\pi}{4})}=2\cdot 2^{\cos x}$$.
A) $$4^{\cos ^{2} (x+\frac{\pi}{4})}=2*2^{\cos x }\Leftrightarrow$$ $$2 ^{2 \cos ^{2}(x+\frac{\pi}{4})}=2^{1+\cos x}\Leftrightarrow$$ $$2 \cos ^{2}(x+\frac{\pi}{4})= 1+\cos x\Leftrightarrow$$ $$2*\frac{1}{2}(1+\cos (2(x+\frac{\pi}{4})))=1+\cos x\Leftrightarrow$$ $$1+\cos(\frac{\pi}{2}+2x)=1+\cos x\Leftrightarrow$$ $$-\sin 2x-\cos x=0\Leftrightarrow$$ $$-2 \sin x \cos x-\cos x=0\Leftrightarrow$$ $$-\cos x(2 \sin x+1)=0\Leftrightarrow$$ $$\left[\begin{matrix}\cos x=0\\\sin x=-\frac{1}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi}{2}+\pi n , n \in Z\\x=-\frac{\pi}{6}+2 \pi k\\x=-\frac{5 \pi}{6}+2 \pi k , k \in Z\end{matrix}\right.$$
Б) На отрезке $$[4 \pi ; \frac{11 \pi}{2}]$$:
$$\frac{\pi}{2}+\pi n$$ : $$4\pi+\frac{\pi}{2}=\frac{9 \pi}{2}$$; $$5 \pi+\frac{\pi}{2}=\frac{11 \pi}{2}$$
$$-\frac{5\pi}{6}+2 \pi n$$ : $$5 \pi+\frac{\pi}{6}=\frac{31 \pi}{6}$$
Задание 14
В правильной треугольной пирамиде SABC точка Е – середина ребра АС, точка Р – середина ребра SВ.
Пусть SH\cap PE=N
A) 1) H-центр $$\Delta ABC \Rightarrow$$ $$BH: HE=2: 1\Rightarrow$$ $$\frac{HE}{EB}=\frac{1}{3}$$
2) для $$\Delta BPE$$ по т. Минелая : $$\frac{SN}{NH}*\frac{HE}{EB}*\frac{BP}{PS}=1\Leftrightarrow$$ $$\frac{SN}{NH}*\frac{1}{3}*\frac{1}{1}=1\Rightarrow$$ $$\frac{SN}{NH}=\frac{3}{1}$$
Б) 1) $$BE\perp AC\Rightarrow$$ $$PE\perp AC$$ (по т. о трех перпендикулярах ), аналогично $$SE\perp AC \Rightarrow$$ $$\angle PES$$ – искомый
2) из $$\Delta ABC$$: $$BE=BC*\sin C=6\sqrt{3}*\frac{\sqrt{3}}{2}=9$$. Из $$\Delta ASE$$: $$SE=\sqrt{AS^{2}-AE^{2}}=$$$$\sqrt{100-27}=\sqrt{73}$$
3) из $$\Delta BSE$$: $$\cos S=\frac{BS^{2}+SE^{2}-BE^{2}}{2 BS*SE}=$$$$\frac{23}{5\sqrt{73}}$$
Из $$\Delta SPE$$: $$PE=\sqrt{SP^{2}+SE^{2}-2 SP*SE*\cos S}=\sqrt{52}$$
Из $$\Delta SPE$$: $$\cos PES=\frac{PE^{2}+SE^{2}-SP^{2}}{2 PE*SE}=$$$$\frac{25}{\sqrt{949}}$$
$$\sin PES=\sqrt{1-\cos ^{2}PES}=$$$$\frac{18}{\sqrt{949}}\Rightarrow$$ $$tg PES=\frac{\sin PES}{\cos PES}=\frac{18}{25}$$
Задание 15
Решите неравенство $$\log_{2} (1-\frac{1}{x})+\log_{2} (10-x) \leq 2$$
ОДЗ: $$\left\{\begin{matrix}1-\frac{1}{x}>0\\10-x>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{x-1}{x}>0\\x<10\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left\{\begin{matrix}x>1\\x<0\end{matrix}\right.\\x<10\end{matrix}\right.\Leftrightarrow$$ $$x \in (-\infty ;0)\cup (1;10)$$
Решение: $$\log_{2}(1-\frac{1}{x})*(10-x)\leq \log_{2}4\Leftrightarrow$$ $$\frac{(x-1)(10-x)}{x}\leq 4\Leftrightarrow$$ $$\frac{10x-x^{2}-10+x-4x}{x}\leq 0\Leftrightarrow$$$$\frac{-x^{2}+7x-10}{x}\leq 0\Leftrightarrow$$ $$\frac{x^{2}-7x+10}{x}\geq 0\Leftrightarrow$$ $$\frac{(x-2)(x-5)}{x}\geq 0 \Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}x>0\\x\leq 2\end{matrix}\right.\\x\geq 5\end{matrix}\right.$$
С учетом ОДЗ: $$x \in (1; 2]\cup [5; 10)$$
Задание 16
Окружность, построенная на стороне BC треугольника ABC как на диаметре, пересекает стороны AB и AC в точках M и N соответственно. Прямые СМ и ВN пересекаются в точке Р. Точка О – середина АР.
A) 1) $$\angle BMC=90$$ (вписанный , опирается на диаметр) $$\Rightarrow$$ $$\angle AMP=90\Rightarrow$$ $$\Delta AMP$$ -прямоугольный $$\Rightarrow$$ $$MO=\frac{1}{2} AP$$(медиана в прямоугольном треугольнике к гипотенузе)
2) аналогично , $$ON=\frac{1}{2} AP\Rightarrow$$ $$OM=ON\Rightarrow$$ $$\Delta MON$$ - равнобедренный
Б) 1)$$\Delta AMN\sim \Delta ABC\Rightarrow$$ $$\frac{AM}{AC}=\frac{AN}{AB}\Rightarrow$$ $$AC=\frac{3*12}{4}=9\Rightarrow$$ $$NC=5$$
2) из $$\Delta BAN$$: $$BN^{2}=AB^{2}-AN^{2}=128$$. Из $$\Delta NCB$$: $$BC=\sqrt{NC^{2}+BN^{2}}=\sqrt{153}\Rightarrow$$ $$MK=KN=\frac{\sqrt{153}}{2}$$(радиусы)
3) $$\Delta AMN\sim \Delta ABC\Rightarrow$$ $$\frac{AM}{AC}=\frac{NM}{CB}\Rightarrow$$ $$NM=\frac{AM}{AC}*CB=\frac{\sqrt{53}}{3}$$
4) Пусть $$NM\cap OK=H$$ , т.к. $$OM=ON$$ , то OM и ON –касательные $$\Rightarrow$$ $$KM\perp OM$$; $$KN\perp ON$$ ; $$\Delta OMK=\Delta ONK$$ ; $$NH=HM=\frac{NM}{2}=\frac{\sqrt{153}}{6}$$
5) из $$\Delta HMK \sin K=\frac{HM}{MK}=\frac{1}{3}\Rightarrow$$$$\cos K=\frac{2\sqrt{2}}{3}\Rightarrow$$$$HK=MK*\cos K=\frac{\sqrt{153}}{2}*\frac{2\sqrt{2}}{3}=\sqrt{34}$$
6) MH – высота $$\Rightarrow$$ $$\Delta OMH \sim \Delta MHK\Rightarrow$$ $$\frac{OH}{HM}=\frac{HM}{HK}\Rightarrow$$$$OH=\frac{153}{36} :\sqrt{34}=\frac{17}{4\sqrt{34}}=\frac{\sqrt{34}}{8}$$
7) $$S_{NOM}=OH *HM=$$$$\frac{\sqrt{34}}{8}*\frac{\sqrt{153}}{6}=\frac{17\sqrt{2}}{16}$$
Задание 17
Предприниматель Ашот хочет открыть в своём городе несколько кафе. Он подсчитал, что жители города тратят 50 млн. рублей в год на питание в кафе, причём эта сумма делится поровну между всеми кафе, работающими в городе. Известно, что функционирование одного кафе обходится в 2 млн. рублей в год. Какую наибольшую прибыль (в млн. рублей в год) может получить Ашот, если в городе уже работает 9 кафе, открытых другими предпринимателями?
Пусть Ашот откроет x шт . кафе , тогда всего их в городе станет 9+x нет, и прибыль с одного будет составлять: $$\frac{50}{9+x}-2$$ . Тогда общая прибыль его составит : $$f(x)=x(\frac{50}{9+x}-2)$$
Найдем максимальное значение данной функции: $${f}'(x)={(\frac{50x}{9+x}-2x)}'=$$$$\frac{50(9+x)-50x}{(9+x)^{2}}-2=0\Leftrightarrow$$$$\frac{450+50x-50x-2(9+x)^{2}}{(9+x)^{2}}=0\Leftrightarrow$$ $$225-(9+x)^{2}=0\Leftrightarrow$$$$(9+x)^{2}=225\Leftrightarrow$$ $$\left[\begin{matrix}9+x =15\\9+x=-15\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=6\\x=-24\end{matrix}\right.$$
Тогда: $$f_{max}=f(6)=6*(\frac{50}{9+6}-2)=$$$$6(\frac{10}{3}-2)=6*\frac{4}{3}=8$$
Задание 18
Найти все а, при каждом из которых уравнение $$\lg (2-x)\sqrt{2ax-3a^{2}}=x\cdot \lg x$$ имеет ровно два различных корня.
ОДЗ: $$\left\{\begin{matrix}2-x>0\\2ax+3a^{2}\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x<2(1)\\2ax+3a^{2}\geq 0 (2)\end{matrix}\right.$$
Решение: $$\lg(2-x)(\sqrt{2ax+3a^{2}}-x)=0\Leftrightarrow$$ $$\left\{\begin{matrix}\lg(2-x)=0\\\sqrt{2ax+3a^{2}}=x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2-x=1\\\left\{\begin{matrix}2ax+3a^{2}=x^{2}\\x\geq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=1\\\left\{\begin{matrix}\left\{\begin{matrix}x_{2}=3a\\x_{3}=-a\end{matrix}\right.\\x\geq 0\end{matrix}\right.\end{matrix}\right.$$
Т.к. $$x\geq 0$$, то $$x_{2}$$ и $$x_{3}$$ будут одновременно существовать , если $$x_{2}=x_{3}=0\Rightarrow a=0$$, условие двух корней соблюдается. В противном случае решениями будут $$x_{1}$$ и $$x_{2 }$$ или $$x_{1}$$ и $$x_{3}$$. При этом , чтобы было два корня , должно выполняться ОДЗ:
$$\left\{\begin{matrix}\left\{\begin{matrix}x_{1}\in (2)\\x_{2} \in (1)\\x_{2}\geq 0\end{matrix}\right.\\\left\{\begin{matrix}x_{1}\in (2)\\x_{3}\in (1)\\x_{3}\geq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left\{\begin{matrix}2a*1+3a^{2}\geq 0\\0\leq 3a<2\end{matrix}\right.\\\left\{\begin{matrix}2a*1+3a^{2}\geq 0\\0\leq -a<2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left\{\begin{matrix}x \in (-\infty -\frac{2}{3}]\cup [0 +\infty )\\a \in [0 \frac{2}{3})\\\end{matrix}\right.\\\left\{\begin{matrix}a \in (-\infty -\frac{2}{3}]\cup [0 +\infty )\\-2<a\leq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$a \in (-2; -\frac{2}{3}]\cup [0; \frac{2}{3})$$
$$x_{1}$$ и так входит в [0 ;2) , потому проверяется только условие (2) для него , $$x_{2}$$ и $$x_{3}$$ и так получились из (2) , потому проверим (1) для них. При этом учитываем, что $$x_{1}\neq x_{2}$$ и $$x_{1}\neq x_{3}$$, иначе получим 1 корень $$\Rightarrow$$ $$3a\neq 1\Rightarrow$$ $$a\neq \frac{1}{3}$$ и $$-a\neq 1\Rightarrow$$ $$a\neq -1$$. Тогда: $$a \in (-2; -1)\cup (-1 ;-\frac{2}{3}]\cup(0 ;\frac{1}{3})\cup [\frac{1}{3}; \frac{2}{3}]$$
Задание 19
16 учеников пишут контрольную работу, составленную в нескольких вариантах. Их рабочие места расположены в виде квадрата 4х4. Будем называть пару учеников «подозрительной», если они сидят на соседних (по вертикали, горизонтали или диагонали) местах и пишут один и тот же вариант. (Ученик может входить в несколько «подозрительных» пар).
19) A) Да, возможно, например:
Б) Нет, т.к. в квадрате размерностью 2*2 однозначно попадает минимум 1 подозрительная пара:
В) Из Б следует, что в квадрате 4*4 мы можем расположить минимум 5 квадратов 2 *2 $$\Rightarrow$$ минимум 5 подозрительных пар:
Например: