405 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
Задание 1
$$S{ABC}=\frac{AC\cdot ВО}{2}=\frac{21\cdot12}{2}=126.$$
Тогда площадь параллелограмма равна:
$$S{ABCD}=2\cdot S_{ABC}=2\cdot126=252.$$
Задание 2
Осевым сечением конуса есть равнобедренный треугольник АВС с углов при вершине С равным 1200.
Высота конуса есть высота осевого сечения, которая в равнобедренном треугольнике есть биссектриса и медиана.
Тогда угол $$АСО = \frac{АСВ}{2} = \frac{120}{2} = 60^{\circ}, АО = ВО = \frac{АВ}{2}$$
В прямоугольном треугольнике АОС определим длину катета АО через угол и другой катет.
$$\tg AOC =\frac{AO}{OC}$$
$$AO = OC\cdot\tg60 = 4\cdot\sqrt{3} = 4\sqrt{3}$$
Катет АО есть радиус окружности в основании конуса, $$R = АО = 4\sqrt{3}$$
Тогда $$S_{осн}=\pi\cdot R^2=\pi\cdot(4\sqrt{3})^2=\pi\cdot48$$
$$\frac{\pi\cdot48}{\pi}=48$$
Задание 3
По условию вероятность поломки телефона в течение года работы равна $$0,2.$$ Значит, вероятность отсутствия поломки на протяжении года равна $$1-0,2 = 0,8.$$ Следовательно, вероятность того, что телефон не выйдет из строя до истечения трёх лет равна $$0,8\cdot0,8\cdot0,8 = 0,512.$$
Соответственно, искомая вероятность противоположного события, состоящего в том, что телефон сломается до того как пройдёт три года
$$1-0,512 = 0,488.$$
Задание 4
Событие A - батарейка неисправна и вероятность P(A) = 0,02
Событие неА - батарейка неисправна и вероятность P(неА) = 1 - 0,02 = 0,98
Обозначим событие Х - хотя бы 6 батареек исправно и вероятность P(X) ≥ 0,95
Не будем сильно мудрить, а просто решим проверкой:
Возьмем 6 батареек (тут явно исход не устроит, но проверим это)
P(X) = P(неА)⁶ = 0,98⁶ ≈ 0,886 < 0,95
Возьмем 7 батареек:
При этом устроят исходы, что все 7 исправны
Или 6 исправны и 1 не исправна. При этом таких вариантов будет равно 7 (количество возможных выборов 1 неисправной батарейки из 7)
Все данные исходы не совместны. Поэтому итоговая вероятность данных исходов равна сумме вероятностей этих исходов:
Вероятность 7 исправных: = P(неА)⁷ = 0,98⁷ ≈ 0,868
Вероятность 1 не исправная и 6 исправных = 7•P(A)•P(неА)⁶ = 7•0,02•0,98⁶ ≈ 0,124
P(X) ≈ 0,868 + 0,124 = 0,992 > 0,95
Таким образом при 7 батарейках получим вероятность выше заданной
Задание 5
$$2^{\log_3 x^2}\cdot5^{\log_3 x}=400$$
$$2^{2\log_3 x}\cdot5^{\log_3 x}=400$$
$$4^{\log_3 x}\cdot5^{\log_3 x}=400$$
$$(4\cdot5)^{\log_3 x}=20^2$$
$$\log_3 x=2$$
$$x=9$$
Задание 6
$$\sin(\alpha-\frac{\pi}{2})=-\sin(\frac{\pi}{2}-\alpha)=-\cos\alpha=-\frac{2}{3}\Rightarrow \cos\alpha=\frac{2}{3}$$
$$\Rightarrow\sin\alpha=-\sqrt{1-(\frac{2}{3})^2}=-\frac{\sqrt{5}}{3}$$
Тогда $$\sin2\alpha=2\sin\alpha\cos\alpha=2\cdot(-\frac{\sqrt{5}}{3})\cdot\frac{2}{3}=-\frac{4\sqrt{5}}{9}$$
$$\cos2\alpha=1-2\sin^2\alpha=1-2\cdot\frac{5}{9}=-\frac{1}{9}$$
Тогда $$\sqrt{5}\cdot\ctg2\alpha=\sqrt{5}\cdot(-\frac{1}{9}):(-\frac{4\sqrt{5}}{9})=\frac{\sqrt{5}\cdot9}{9\cdot4\sqrt{5}}=\frac{1}{4}=0,25$$
Задание 7
Приравняем уравнения и найдём $$a$$ через $$D,$$ так как общая точка касания одна, значит, одно решение и $$D=0.$$
$$ax^2-21x+3a=7x+28\quad\quad a>0$$
$$ax^2-21x+3a-7x+28=0$$
$$ax^2-28x+3a-28=0$$
$$\frac{D}{4}=(-14)^2-a\cdot(3a-28)=0,$$ т.к. одна точка касания
$$(-14)^2-a\cdot(3a-28)=0$$
$$196-3a^2+28a=0$$
$$-3a^2+28a+196=0$$
$$\frac{D}{4}=14^2-(-3)\cdot196=196+3\cdot196=4\cdot196=2^2\cdot14^2=28^2$$
$$a_1=\frac{-14+28}{-3}=\frac{-14}{3}\notin$$ т.к. $$a>0$$
$$a_2=\frac{-14-28}{-3}=14$$
Задание 8
Найдем расстояния до воды в колодце перед дождем.
Т.к. до дождя время падения камешков составляло 0,8 с, подставим эту величину в формулу, по которой рассчитывается расстояние до воды:
$$h = 5\cdot(0,8)^2 = 3,2$$ м.
Очевидно, что после дождя уровень воды поднимается, значит, время падения камешка уменьшается.
То есть становится равным $$0,8 - 0,3 = 0,5$$ с.
Вычислим расстояние до воды после дождя:
$$h = 5\cdot(0,5)^2 = 1,25$$ м
Уровень воды поднялся на $$3,2-1,25 = 1,95$$ м.
Задание 9
Пусть $$x$$ км - это расстояние, которое проехала вторая машина от места встречи, то есть половина расстояния от места встречи до пункта А. Тогда расстояние от места встречи до пункта А равно $$2x$$ км, а от места встречи до пункта В - $$(40-2x)$$ км. Пусть $$y$$ км/ч - скорость первой машины, тогда $$\frac{2x}{y}$$ ч - время, которое затратила первая машина от пункта А до места встречи, $$\frac{2x}{45}$$ ч - время, которое затратила вторая машина от пункта А до места встречи. Нам также известно, что вторая машина преодолела это расстояние на 20 минут, или на $$\frac{1}{3}$$ часа, быстрее первой. Получаем уравнение:
$$\frac{2x}{y}-\frac{2x}{45}=\frac{1}{3}\quad (1)$$
Теперь работаем со второй частью пути. Время, которое первая машина затратила на путь от места встречи до пункта В - $$\frac{40-2x}{y}$$ ч. За такое же время вторая машина преодолела $$x$$ км, то есть затратила $$\frac{x}{45}$$ ч. Получаем второе уравнение системы:
$$\frac{40-2x}{y}=\frac{x}{45}\quad (2)$$
Работаем со вторым уравнением, нам нужно выразить $$x.$$
$$\frac{40-2x}{x}=\frac{y}{45}$$
$$\frac{40}{x-2}=\frac{y}{45}$$
$$\frac{40}{x}=\frac{y}{45+2}$$
$$\frac{40}{x}=\frac{y+90}{45}$$
$$x=\frac{1800}{y+90}$$
Теперь подставим x в первое уравнение:
$$\frac{2\cdot\frac{1800}{y+90}}{y}-2\cdot\frac{\frac{1800}{y+90}}{45}=\frac{1}{3}$$
$$\frac{3600}{y\cdot (y+90)}-\frac{3600}{45\cdot(y+90)}=\frac{1}{3}$$
$$\frac{3600}{y\cdot (y+90)}-\frac{80}{y+90}=\frac{1}{3}$$
Домножим на $$y$$ и $$(y+90)$$
$$10800-240y=y^2+90y$$
$$y^2+330y-10800=0$$
Получили квадратное уравнение. Решаем через дискриминант.
$$D=330^2-4\cdot1\cdot(-10800)=108900+43200=152100$$
$$y_1=\frac{-330-\sqrt{152100}}{2\cdot1}=\frac{-330-390}{2}=\frac{-720}{2}=-390$$ - отрицательный корень не подходит.
$$y_2=\frac{-330+\sqrt{152100}}{2\cdot1}=\frac{-330+390}{2}=\frac{60}{2}=30$$ км/ч - скорость первой машины.
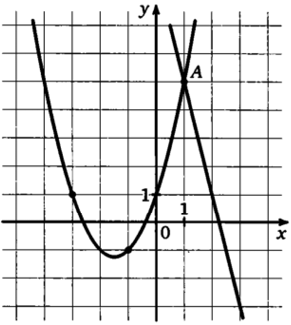
Задание 10
График g(x) проходит (-1;-1); (-3;1) и (0;1).
Получим:
$$\left\{\begin{matrix} -1=a(-1)^2+b(-1)+c\\ 1=a(-3)^2+b(-3)+c\\ 1=a\cdot0+b\cdot0+c \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a-b=-2\\ 9a-3b=0\\ c=1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=3\\ a=1\\ c=1 \end{matrix}\right.$$
Получили: $$g(x)=x^2+3x+1$$
Тогда $$x^2+3x+1=-4x+9\Leftrightarrow x^2+7x-8=0 \Rightarrow\left[\begin{matrix} x=-8\\ x=1 \end{matrix}\right.$$
Задание 11
$$((17-6\sqrt{x})e^{1-x})'=(17-6\sqrt{x})'e^{1-x}+(e^{1-x})'(17-6\sqrt{x})=$$
$$=-\frac{6}{2\sqrt{x}}e^{1-x}-e^{1-x}(17-16\sqrt{x})=-e^{1-x}(\frac{3}{\sqrt{x}})+17-6\sqrt{x})$$
Пусть $$\frac{3}{\sqrt{x}}+17-6\sqrt{x}=0.$$ Пусть $$\sqrt{x}=a>0:$$
$$\frac{3}{a}+17-6a=0\Rightarrow \frac{-6a^2+17a+3}{a}=0$$
$$D=289+72=361$$
$$a_1=\frac{-17+91}{-12}=-\frac{1}{6};\quad a_2=\frac{-17-91}{-12}=3.$$
Получим: $$\sqrt{x}=3\Rightarrow x=9.$$
При $$x=4: \frac{3}{2}+17-6\cdot2>0.$$ С учётом с $$-e^{1-x}$$ получим отрицательное значение y'.
При $$x=16: \frac{3}{4}+17-6\cdot4<0\Rightarrow y'>0.$$ Т.е. $$x=9$$ - точка минимума.