305 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.

Три числа относятся как 5:6:10. Если первое число уменьшить на 10%, а второе — на 20%, то на сколько процентов надо увеличить третье число, чтобы их сумма не изменилась?

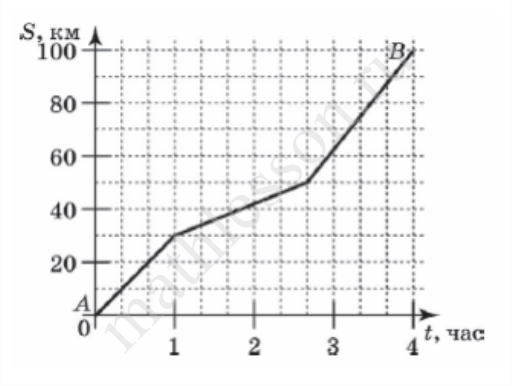
На рисунке изображен график, описывающий прямолинейное движение автобуса. По горизонтальной оси отложено время (в часах), по вертикальной — расстояние от пункта А (в километрах). Выехав из пункта A в пункт B, автобус через некоторое время должен был снизить скорость из‐за ремонта шоссе. Используя график движения автобуса, определите длину ремонтируемого участка шоссе (в километрах).

В параллелограмме ABCD известны координаты трех вершин: A(–1; 3), B(2; 4), C(7; 8). Найдите ординату точки D.

В первой коробке 20 ламп, из них 18 стандартных. Во второй коробке – 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найдите вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.

Решите уравнение $$\log_{30-3\cdot2^x}(2^x-3)^2=\log_{2^x-2}(2^x-3)^2$$. Если корней несколько, в ответе укажите их сумму.

Найдите длину общей касательной двух окружностей, радиусы которых равны 4 и 1, касающихся внешним образом

На рисунке изображен график некоторой функции $$y=f(x)$$. Одна из первообразных этой функции равна $$F(x)=-\frac{1}{3}x^{3}-\frac{5}{2}x^2-4x+2$$. Найдите площадь заштрихованной фигуры.

Площадь боковой поверхности конуса равна 16 см². Радиус основания конуса уменьшили в 4 раза, а образующую увеличили в 2 раза. Найдите площадь боковой поверхности получившегося конуса. Ответ дайте в см².

Найдите значение выражения $$\log_{\sqrt{ab}}\frac{\sqrt[5]{a}}{\sqrt[8]{b}}$$, если $$\log_{ab}a=5$$

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой m=6 кг и радиуса R=15 см, и двух боковых с массами M=1 кг и с радиусами R+h . При этом момент инерции катушки относительно оси вращения, выражаемый в кг ∙ см² , задаeтся формулой $$I=\frac{(m+2M)R^2}{2}+M(2RH+h^{2})$$. При каком максимальном значении h момент инерции катушки не превышает предельного значения 1300 кг ∙ см²? Ответ выразите в сантиметрах

В баке находится 100 литров смеси кислоты с водой. Из бака отлили часть смеси и добавили равное по объёму количество воды, которое на 10 литров превышает первоначальное количество кислоты в смеси. Затем снова отлили такое же количество смеси, как в первый раз, в результате чего количество кислоты в баке уменьшилось в четыре раза по сравнению с количеством её в исходной смеси. Определить количество воды в исходной смеси в литрах.

Найдите точку минимума функции $$y=5\frac{3}{4}+3x+\frac{x^2}{2}-x^{3}-\frac{x^{4}}{4}$$

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ АВ:BC:CC₁=1:2:3

Решите неравенство: $$-\log_{\frac{x}{6}}(\frac{\lg\sqrt{6-x}}{\lg x})>\lg\frac{|x|}{x}$$

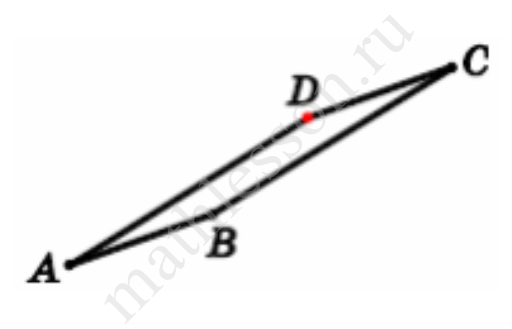
На основании АС равнобедренного треугольника АВС расположена точка D так, что AD=2, CD=1. Окружности, вписанные в треугольники ABD и DBC, касаются прямой BD в точках M и N соответственно.

15 января планируется взять кредит в банке на сумму 600000 рублей на 24 месяца. Условия его возврата таковы:

На сколько рублей увеличится сумма выплат, если взять кредит с теми же условиями на 30 месяцев?

Найдите все значения a , при которых уравнение $$x^{2}+2a=x+|x^2-a|$$ имеет три корня

В фирме имеется n отделов, в одном из которых работает 1/8 сотрудников, в другом ‐ 210 сотрудников, а численность каждого из оставшихся отделов составляет 1/9 от всей численности сотрудников фирмы.