250 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Решаем ЕГЭ 250 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №250 (alexlarin.com)
Решаем ЕГЭ 250 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №250 (alexlarin.com)
Задание 1
В салоне парфюмерии проходит акция: покупая флакон духов объёмом 100 мл, покупатель получает в подарок флакон духов объёмом 30 мл. Какой наибольший объём (в мл) духов можно получить за 7000 рублей во время этой акции, если флакон духов объёмом 100 мл стоит 1800 рублей, объёмом 50 мл – 1200 рублей, а объёмом 30 мл – 800 рублей?
На 7000 рублей можно купить 3 флакона по 100 мл. и 2 по 30 мл.
В итоге купил 350 мл. При этом в подарок получим : 3*30=90мл.
Итого: 360+90=450
Задание 2
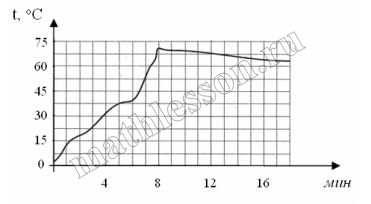
На графике показан процесс разогрева двигателя легкового автомобиля при температуре окружающего воздуха 5°С. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Когда температура достигает определённого значения, включается вентилятор, охлаждающий двигатель, и температура начинает понижаться. Определите по графику, сколько минут прошло с момента запуска двигателя до включения вентилятора?
С момента, когда включится вентилятор, температура двигателя должна понижаться (если у вас не автоваз). Понижение температуры начинается с 8 минуты
Задание 3
Найдем площадь сектора большого круга : $$S_{1}=\frac{\pi R^{2}}{360}\alpha$$, $$\alpha =45; R=2\Rightarrow$$ $$S_{1}=\frac{\pi*4}{360}*45 =\frac{\pi}{2}$$
Площадь сектора маленького круга : $$S_{2}=\frac{\pi*1}{360}*45 =\frac{\pi}{8}$$
Тогда площадь закрашенного: $$S=S_{B}-S_{M}-S_{1}+S_{2}$$, где
$$S_{B}=\pi *2^{2}=4 \pi$$ – площадь большого круга
$$S_{M}=\pi *1^{2}=\pi$$ - площадь малого круга
$$S=-4 \pi -\pi -\frac{\pi}{2}+\frac{\pi}{8}=\frac{21 \pi}{8}$$. При этом $$S_{B}=24$$. Тогда
$$4\pi-24$$
$$\frac{21 \pi}{8}-x$$
$$x=\frac{\frac{21 \pi}{8}*24^{3}}{4 \pi}=15, 75$$
Задание 4
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Общее количество исходов: $$N=6^{3}$$ исходы с выпадением 16 очков: 466;565;556;655;664;646 $$\Rightarrow$$ 6 исходов . Тогда вероятность: $$P=\frac{6}{6^{3}}=$$$$\frac{1}{6^{2}}=\frac{1}{36}\approx 0, 03$$
Задание 5
Найдите корень уравнения $$(\frac{1}{8})^{-3+x}=512$$
$$(\frac{1}{8})^{-3x+x}=512\Leftrightarrow$$$$(\frac{1}{8})^{-3x+x}=8^{3}\Leftrightarrow$$ $$(\frac{1}{8})^{-3x+x}=(\frac{1}{8})^{-3}\Leftrightarrow$$ $$-3x+x=-3\Leftrightarrow$$ $$x=0$$
Задание 6
В треугольнике АВС угол А равен 30, а угол С равен 105. Найдите АС, если $$BC=3\sqrt{2}$$ .
$$\angle B=180-105-30=45$$. По т. синусов: $$\frac{AC}{\sin B}=\frac{BC}{\sin A}\Rightarrow$$ $$AC=\frac{BC*\sin B}{\sin A}=$$$$\frac{3\sqrt{2} \frac{\sqrt{2}}{2}}{\frac{1}{2}}=6$$
Задание 7
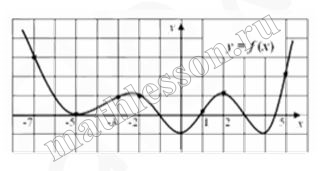
На графике функции у = f (x) отмечены семь точек с абсциссами ‐7, ‐5, ‐3, ‐2, 1, 2, 5. Определите по данному графику, в какой из этих точек значение производной f'(x) наибольшее. (В ответе укажите абсциссу этой точки).
Если f(x) возрастает , то $$f}(x)>0$$. Чем быстрее возрастает, тем больше $$f'(x)\Rightarrow$$ $$f'_{max}={f}'(5)$$
Задание 8
В правильной шестиугольной пирамиде PАВСDEF сторона основания равна 2, а боковое ребро равно$$\sqrt{6}$$. Найдите площадь сечения пирамиды плоскостью РАС.
Из $$\Delta ABC$$ : $$AC=\sqrt{AB^{2}+BC^{2}-2 BC*AB\cos B}=$$$$\sqrt{2^{2}+2^{2}-2*2*2*(-\frac{1}{2})}=\sqrt{12}$$ Из $$\Delta APC$$ : $$AP^{2}+PC^{2}=AC^{2}\Rightarrow$$$$\Delta APC$$ - прямоугольный и $$S_{APC}=\frac{1}{2}\sqrt{6}\sqrt{6}=3$$
Задание 9
Найдите значение выражения $$6x(3x^{12})^{3}:(3x^{9})^{4}$$ при x = 75
$$6x*(3x^{12})^{3}:(3x^{9})^{4}=$$$$\frac{6x*3^{3}*x^{36}}{3^{4}*36}=$$$$2x=2*75=150$$
Задание 10
При вращении ведёрка с водой на верёвке в вертикальной плоскости вода не выливается из него, если сила её давления на дно ведёрка неотрицательна во всех точках траектории. В верхней точке траектории сила давления воды на дно минимальна и равна $$P=m(\frac{v^{2}}{L}-g)$$, где m – масса воды в кг, v – скорость движения ведёрка в м/с, L – длина веревки в метрах, g = 10 м/с2 – ускорение свободного падения. С какой минимальной скоростью v надо вращать ведёрко, чтобы вода не выливалась из него, если длина веревки равна 57,6 см? Ответ дайте в м/с.
Раз вода не выливается , значит $$P\geq 0$$. При $$v\rightarrow max ; P\rightarrow 0$$, следовательно:
$$0=m*(\frac{v^{2}}{L}-g)\Leftrightarrow$$ $$\frac{v^{2}}{L}-g=0$$.
Расстояние в формуле дается в метрах, потому: L=57,6 см =0,576м
$$\frac{v^{2}}{0,576}-10=0\Leftrightarrow$$ $$v^{2}=5,76\Leftrightarrow v=2,4$$м\с
Задание 11
Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов теста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?
Пусть x- кол-во вопросов в тесте. Тогда : время Пети : $$t_{2}=\frac{x}{8}$$; Вани : $$t_{2}=\frac{x}{9}$$. При этом $$t_{1}-t_{2}=20$$ минут $$=\frac{1}{3}$$ часа.
$$\frac{x}{8}-\frac{x}{9}=\frac{1}{3}\Leftrightarrow$$ $$\frac{9x-8x}{8*9}=\frac{1}{3}\Leftrightarrow$$ $$\frac{x}{8*9}=\frac{1}{3}\Leftrightarrow$$ $$x=\frac{8*9}{3}=24$$ вопроса
Задание 12
Найдите наименьшее значение функции $$f(x)=x^{3}-3x^{2}-9x+31$$ на отрезке [-1;4]
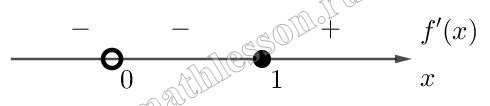
Найдем производную и приравняем ее к нулю: $$f'(x)=3x^{2}-6x-9=0\Leftrightarrow$$$$x^{2}-2x-3=0\Leftrightarrow$$$$\left\{\begin{matrix}x_{1}+x_{2}=2\\x_{1}*x_{2}=-3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=3\\x_{2}=-1\end{matrix}\right.$$
При этом х=3 - является точкой минимума (х=-1 - точка максимума). Тогда минимальное значение функции: $$f_{min}=f(3)=3^{3}-3*3^{2}-9*3+31=4$$
Задание 13
А) Замена : $$(\frac{6}{5})^{\cos 3x}=y>0\Rightarrow$$ $$(\frac{5}{6})^{\cos 3x}=\frac{1}{y}$$
$$y+\frac{1}{y}=2\Leftrightarrow$$ $$\frac{y^{2}-2y+1}{y}=0\Leftrightarrow$$ $$\frac{(y-1)^{2}}{y}=0\Leftrightarrow$$ $$y-1=0\Leftrightarrow$$ $$y=1$$
$$(\frac{6}{5})^{\cos 3x}=1\Leftrightarrow$$ $$\cos 3x=0 \Leftrightarrow$$ $$3x=\frac{\pi}{2}+\pi n , n \in Z \Leftrightarrow$$ $$x=\frac{\pi}{6}+\frac{\pi n }{3}, n \in Z$$
Б) На заданном промежутке имеем единтвенный корень: $$4 \pi +\frac{\pi}{6}=\frac{25 \pi}{6}$$
Задание 14
Правильная треугольная призма АВСА1В1С1 пересечена плоскостью, проходящей через середины ребер АВ, А1С1, ВВ1. Сторона основания призмы равна 2, а высота призмы равна $$\frac{\sqrt{7}}{7}$$ .
A) 1) Введем ортогональную систему координат, как на рисунке .
2) Зададим уравнение плоскости сечения. Для этого найдем координаты трех точек, лежащих в данной плоскости:
$$N_{x}=-\frac{1}{2}KA=-\frac{1}{2};$$ $$N_{y}=\frac{1}{2}KB=\frac{\sqrt{3}}{2}$$; $$N_{z}=0$$
$$K_{x}=0$$; $$K_{y}=0$$; $$K_{z}=CC_{1}=\frac{\sqrt{7}}{7}$$
$$M_{x}=0$$; $$M_{y}=KB=\sqrt{3}$$; $$M_{z}=\frac{1}{2}CC_{1}=\frac{\sqrt{7}}{14}$$
Тогда : $$\left\{\begin{matrix}-\frac{1}{2}a+\frac{\sqrt{3}}{2}b+d=0\\\frac{\sqrt{7}}7{c+d=0}\\\sqrt{3}b+\frac{\sqrt{7}}{14}=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{1}{2}a+\frac{\sqrt{3}}2{b+d=0}\\c=-\sqrt{7}d\\\sqrt{3}b-\frac{7d}{14}+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}-\frac{1}{2}a-\frac{1}{4}d+d=0\\c=-\sqrt{7}d\\b=-\frac{1}{2\sqrt{3}}d\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a=\frac{3}{2}d\\b=-\frac{1}{2\sqrt{3}}d\\c=-\sqrt{7}d\end{matrix}\right.$$
Тогда нормаль-вектор для $$(NMK_{1})$$: $$\bar{n}(\frac{3}{2};-\frac{1}{2\sqrt{3}}; -\sqrt{7})$$
Нормаль-вектор для (ABC)-ось OZ: $$\bar{m}(0;0;1)$$
3) $$\cos(\bar{n},\bar{m})=\frac{\left | \frac{3}{2}*0-\frac{1}{2\sqrt{3}}*0-\sqrt{7}*1 \right |}{\sqrt{(\frac{3}{2})^{2}+(-\frac{1}{2\sqrt{3}})^{2}+(-\sqrt{7})^{2}}\sqrt{1^{2}}}=$$$$\frac{\sqrt{3}}{2}\Rightarrow$$ $$\angle (\bar{n},\bar{m})=30$$, что так же является углом между плоскостями
Б) 1) AN=NB; $$\angle ANE=\angle MNB\Rightarrow$$ $$\Delta ANE=\Delta NMB$$ и $$AE=MB=\frac{1}{2} BB_{1}=\frac{\sqrt{7}}{14}$$
2) $$\Delta ALE\sim \Delta A_{1}EK_{1}\Rightarrow$$ $$\frac{AL}{A_{1}K_{1}}=\frac{AE}{A_{1}E}=\frac{1}{3}\Rightarrow$$ $$AL=\frac{1}{3}\Rightarrow$$$$S_{\Delta ALN}=\frac{1}{2}*\frac{1}{3}*1*\frac{\sqrt{3}}{2}=$$$$\frac{\sqrt{3}}{12}(\frac{1}{2}AL*AN\sin A)$$
3)Проведем из B прямую $$\left | \right |NL\Rightarrow BQ$$: $$\frac{AN}{NB}=\frac{AL}{LQ}\Rightarrow$$ $$LQ=AL=\frac{1}{3}\Rightarrow$$ $$QK=1-2*\frac{1}{3}=\frac{1}{3}$$
4) $$\Delta KCR\sim \Delta QCB($$R-проекция $$R_{1}$$, $$K_{1}R_{1}\left | \right |KR$$, но $$K_{1}R_{1}\left | \right |LN\Rightarrow$$ $$K_{1}R_{1}\left | \right |QB\Leftrightarrow$$ $$KR\left | \right |QB$$)$$\Rightarrow S_{KCR}=S_{QCB}$$($$\frac{CK}{CQ})^{2}$$. $$S_{QCB}=\frac{1}{2}*\frac{4}{3}*2*\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}$$. $$(\frac{CK}{CQ})^{2}=(\frac{1}{\frac{4}{3}})^{2}=\frac{9}{16}$$. $$S_{KCR}=\frac{2\sqrt{3}}{3}*\frac{9}{16}=\frac{3\sqrt{3}}{8}$$
5) $$S_{\angle NBRK}=S_{ABC}-S_{ALN}-S_{CKR}$$
$$S_{ABC}=\frac{1}{2}*2*2*\frac{\sqrt{3}}{2}=\sqrt{3}$$
$$S_{\angle NBRK}=\sqrt{3}-\frac{\sqrt{3}}{12}-\frac{3\sqrt{3}}{8}=\frac{13\sqrt{3}}{24}$$
Но LNBRK-проекция $$K_{1}LNMR_{1}$$ на $$(ABC)\Rightarrow S_{K_{1}LNMR_{1}}=$$$$\frac{S_{\angle NBRK}}{\cos\alpha }$$,где $$\alpha =30$$
$$S_{K_{1}LNMR_{1}}=\frac{13\sqrt{3}}{24}:\frac{\sqrt{3}}{2}=\frac{13}{12}$$
Задание 15
Решите неравенство: $$\frac{1}{4}x^{\frac{1}{2}\log_{2} x}\geq 2^{\frac{1}{4}\log_{2} ^{2} x}$$
ОДЗ: $$x>0$$
$$\frac{1}{4} * x^{\frac{1}{2}\log_{2}x}\geq 2 ^{\frac{1}{4} \log_{2}^{2}x}|:\frac{1}{4}\Leftrightarrow$$$$x^{\frac{1}{2}\log_{2}x}\geq 2^{2+\frac{1}{4}\log_{2}^{2}x}$$
Введем замену: $$\frac{1}{2}\log_{2}x=y\Rightarrow \log_{2}x=2y\Rightarrow x=2^{2y}$$
$$(2^{2y})^{y}\geq 2^{2+y^{2}}\Leftrightarrow 2^{2y^{2}}\geq 2^{2+y^{2}}\Leftrightarrow 2y^{2}\geq 2+y^{2}\Leftrightarrow y^{2}\geq 2\Leftrightarrow$$ $$\left[\begin{matrix}y\geq \sqrt{2}\\y\leq -\sqrt{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\frac{1}{2}\log_{2}x\geq \sqrt{2}\\\frac{1}{2}\log_{2}x\leq -\sqrt{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\log_{2}x\geq 2\sqrt{2}\\\log_{2} x \leq -2\sqrt{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x \geq 2^{2\sqrt{2}}\\x \leq \frac{1}{2^{2\sqrt{2}}}\end{matrix}\right.$$
С учетом ОДЗ: $$x \in (0, \frac{1}{2^{2\sqrt{2}}}]\cup [2^{2\sqrt{2}}, +\infty )$$
Задание 16
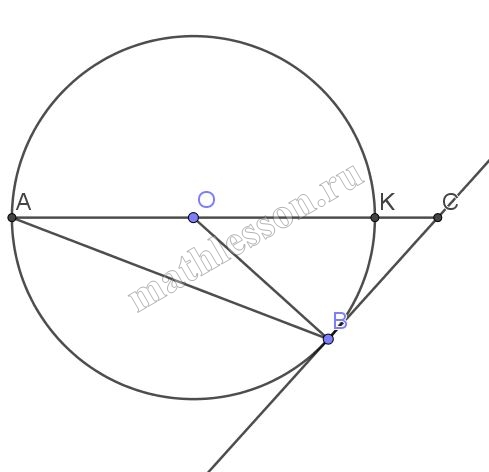
В окружности с центром в точке О радиуса 4 проведены хорда АВ и диаметр АК, образующий с хордой угол $$\frac{\pi}{8}$$ . В точке В проведена касательная к окружности, пересекающая продолжение диаметра АК в точке С.
A) 1) $$\angle KAB=\frac{1}{2}KOB\Rightarrow$$ $$\angle KOB=2*\frac{\pi}{8}=\frac{\pi}{4}$$ (вписанный и центральный, опирающиеся на одну дугу)
2) Радиус в точку касания, проведенный, перпендикулярен касательной: $$OB\perp BC\Rightarrow$$$$\Delta OBC$$ - прямоугольный$$\Rightarrow \angle OCB=\frac{\pi}{2}-\angle COB=\frac{\pi}{4}\Rightarrow$$ $$\Delta OCB$$ - равнобедренный
Б) 1) $$OB=BC=4\Rightarrow$$ $$\Delta OCB:OC=\sqrt{4^{2}+4^{2}}=4\sqrt{2}\Rightarrow$$ $$AC=4+4\sqrt{2}$$
2) $$CM=\frac{1}{2}CB=2\Rightarrow$$ из $$\Delta ACM:AM=\sqrt{AC^{2}+CM^{2}-2 AC*CM \cos C}=$$$$\sqrt{(4+4\sqrt{2})^{2}+2^{2}-2*2(4+4\sqrt{2})*\frac{\sqrt{2}}{2}}=$$$$\sqrt{36+24\sqrt{2}}=2\sqrt{9+6\sqrt{2}}$$
Задание 17
Производительность первого цеха завода не более 730 произведённых телевизоров в сутки. Производительность второго цеха завода до реконструкции составляла 75% от производительности первого цеха. После реконструкции второй цех увеличил производительность на 20% и стал выпускать более 640 телевизоров в сутки. Найдите, сколько телевизоров в сутки выпускает второй цех после реконструкции, если оба цеха выпускают в сутки целое число телевизоров.
Пусть x - число телевизоров в сутки 1-го цеха $$x\leq 730$$ . Тогда 0,75x - второй цех до реконструкции. После реконструкции : $$0,75*1,2=0,9 x$$. При этом $$0,9x>640$$
Получим: $$\left\{\begin{matrix}x\leq 730\\0,9x>640\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\leq 730\\x>711,(1)\end{matrix}\right.$$
При этом $$0,9x \in N$$ и $$0,75x \in N$$ (т.к. выпускается целое число телевизоров ). С учетом, что $$x \in [712; 730]$$ получаем, что $$0,9 x \in N$$ при x=729 или x=720. Но $$0,75x \in N$$ только при $$x =720\Rightarrow 720*09=648$$ - второй.
Задание 18
Найдите все значения параметра a при которых уравнение $$\sqrt[3]{\frac{1}{2}x^{3}+x+1}+\sqrt[3]{-\frac{1}{2}x^{3}+x-1}=\sqrt[3]{ax}$$ имеет ровно четыре корня
Вынесем $$\sqrt[3]{x}:$$ $$\sqrt[3]{x}(\sqrt[3]{1+\frac{1}{x}+\frac{x^{2}}{2}}+\sqrt[3]{1-\frac{1}{x}-\frac{x^{2}}{2}})=\sqrt[3]{x}*\sqrt[3]{a}$$
Следовательно, $$\sqrt[3]{x}=0\Leftrightarrow x=0$$ является корнем, значит надо еще три отличных от 0 корня.
Введем замену : $$\frac{x^{2}}{2}+\frac{1}{x}=t$$. Тогда: $$\sqrt[3]{1+t}+\sqrt[3]{1-t}=\sqrt[3]{a}$$
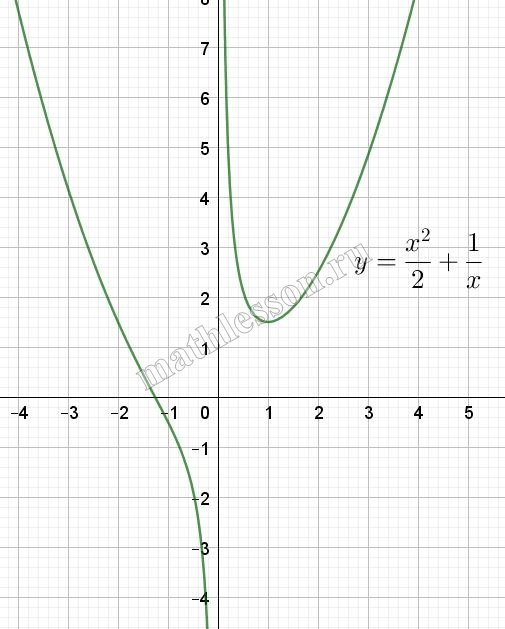
Рассмотрим замену: пусть $$f(x)=\frac{x^{2}}{2}+\frac{1}{x}$$ и g(x)=t. g(x)=t – прямая, параллельная Ox. При этом f(x)-совмещенный график параболы и обратной пропорциональности. Исследуем график:
$$f(x)=0\Leftrightarrow$$ $$\frac{x^{2}+2}{2x}=0\Leftrightarrow$$ $$x=-\sqrt[3]{2}$$
$$f'(x)=0\Leftrightarrow$$ $$x-\frac{1}{x^{2}}=0\Leftrightarrow$$ $$\frac{x^{3}-1}{x^{2}}=0$$
$$x=1$$ –точка минимума. При x=1: $$f(1)=\frac{1}{2}+1=1,5$$.
$$lim_{x\rightarrow -\infty} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$; $$lim_{x\rightarrow +\infty} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$
$$lim_{x\rightarrow -0} (\frac{x^{2}}{2}+\frac{1}{x})=-\infty$$; $$lim_{x\rightarrow +0} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$.
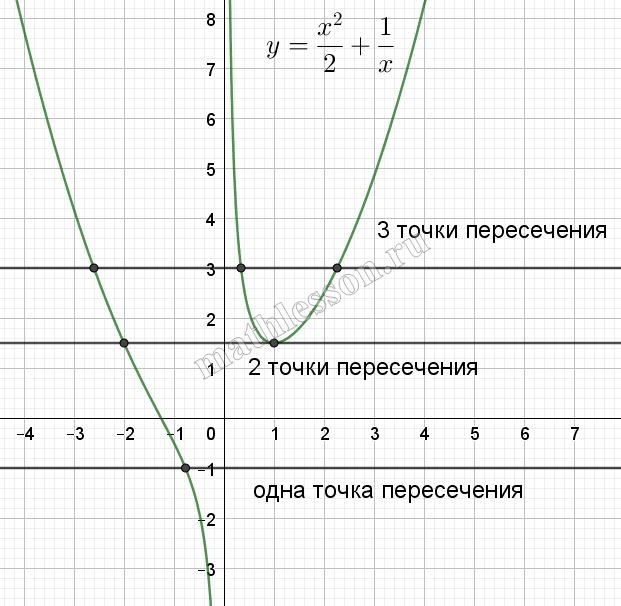
При x=1: $$f(1)=\frac{1}{2}+1=1,5$$. Построим эскиз :
Видим что при t<1,5-одно решение, при t=1,5-два решения , при t>1,5 – три решения.
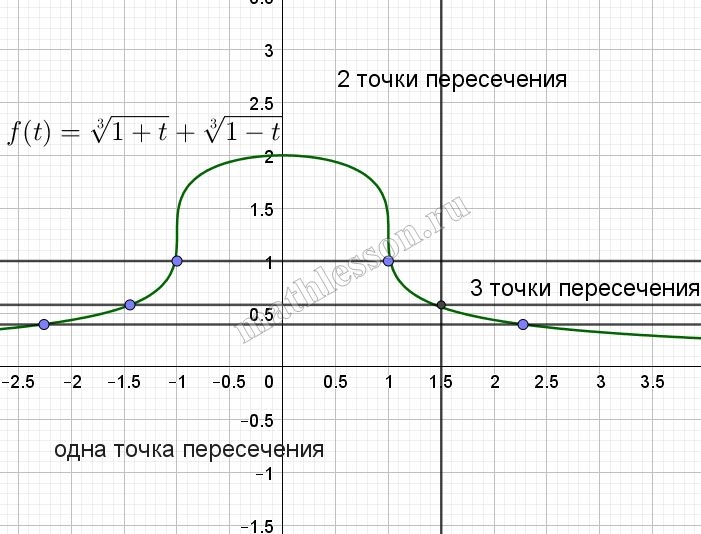
Рассмотрим уравнение: $$\sqrt[3]{t+1}+\sqrt[3]{1-t}=\sqrt[3]{a}$$. Пусть $$f(t)=\sqrt[3]{1+t}+\sqrt[3]{1-t}; g(t)=\sqrt[3]{a}$$
Построим график :
Каждое пересечение при t<1,5 , дает одно решение, при t>1,5 даёт три решения и т.е. есть всегда 1(при t<0) , то нас не устраивает .
При t=1,5 будет 2 решения, да еще одно ( область t<0)-следовательно, в общем получим 3, что и нужно .
Найдем a : $$\sqrt[3]{1+\frac{3}{2}}+\sqrt[3]{1-\frac{3}{2}}=\sqrt[3]{a}$$
$$\sqrt[3]{\frac{5}{2}}-\sqrt[3]{\frac{1}{2}}=\sqrt[3]{a}\Leftrightarrow$$ $$\frac{\sqrt[3]{5}-1}{\sqrt[3]{2}} =\sqrt[3]{a}\Leftrightarrow$$ $$a=\frac{(\sqrt[3]{5}-1)^{3}}{2}$$
Задание 19
A) Пусть $$n=10a+b$$ , тогда $$n +24=10(a+2)+(b+4)$$ или $$n+24=10(a+3)+(b+4-10)$$ (если n оканчивается на число $$\geq 6$$). Рассмотрим первый вариант. Одинаковый остаток при делении на 100 дадут 2 числа, одно из которых оканчивается на 1, второе на 9 ( 2 и 8; 3 и 7; 4 и 6) .Как видим, для первого варианта (b и b+4) устраивают окончания 3 и 7 . Тогда $$n=10a+3$$,
$$n+24=10(a+2)+7$$. Тогда $$n^{2}=100x^{2}+60x+9$$; $$(n+24)^{2}=100x^{2}+540x+729$$
При делении на 100 у $$n^{2}$$ остаток $$60x+9$$, у $$(n+24)^{2}$$: $$540x+729$$. При этом, они отличаются на натуральное число : $$\frac{540x+729}{100}=N+\frac{69x+9}{100}\Leftrightarrow$$$$N=\frac{480x+720}{100}=\frac{48x+72}{10}$$. Откуда $$x=1$$ или 6 .То есть число 13 или 63.
Б) Если остатки одинаковы, то разность этих чисел кратна 100: $$\frac{(n+24)^{2}-n^{2}}{100}\in N \Rightarrow$$ $$\frac{24(2n+24)}{100}\in N \Leftrightarrow$$ $$\frac{12(n+12)}{25}\in N$$. Т.к. n $$\in [100; 999]$$ , то $$n+12\in [112;1011]$$. При этом, кратных 25 там: $$\frac{1011-111}{25}=36$$ чисел.
B) $$m \in [10;99], n \in [100; 999]$$. Ищем аналогично Б): $$\frac{(n+m)^{2}-n^{2}}{100}\in N \Leftrightarrow$$ $$\frac{m(2n+m)}{100}\in N$$. В данном случае m-четное( иначе не будет кратно 100-четному) .Путсь $$m=2k : k \in [\frac{10}{2}, \frac{99}{2}]\Leftrightarrow [5;49]$$. $$\frac{2k(2n+2k)}{100}\Leftrightarrow$$ $$\frac{k(n+k)}{25}\in N$$
При k кратному 5 получаем, что n+k тоже кратно 5, а таких чисел больше. Тогда k-не кратно 5, следовательно , n+k кратно 25. С учетом , что $$n \in [100; 999]$$, то $$n+k \in [100+k; 999+k]$$, тогда кратных к 25 среди них: $$\frac{999+k-(99+k)}{25}=36$$. Т.е. все числа [5;49] не кратных 5 подойдут, а их 36.