246 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Если 30% в младшей, то 100-30=70% в средней и старшей школах. Найдем количество учеников там: 100*0,7=560 человек.

     Так как изучают 20%, то это значение составляет: 560*0,2=112 человек

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

На момент запуска (0 минут) давление составляло 1 атм

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

 Используя теоремы Пифагора, найдем стороны треугольника AOB из прямоугольных треугольников:

$$BO=\sqrt{1^{2}+3^{2}}=\sqrt{10}$$

$$OA=\sqrt{2^{2}+2^{2}}=\sqrt{8}$$

$$BA=\sqrt{5^{2}+1^{2}}=\sqrt{26}$$

     Из теоремы косинусов:

$$\Delta OAB \cos BOA=\frac{OB^{2}+OA^{2}-AB^{2}}{2*OB*OA}=$$$$\frac{10+8-26}{2*\sqrt{10}*\sqrt{8}}=\frac{-8}{2*4\sqrt{5}}=$$$$-\frac{1}{\sqrt{5}}$$

     По основному тригонометрическому тождеству:

$$\sin BOA=\sqrt{1-(-\frac{1}{\sqrt{5}})^{2}}=\frac{2}{\sqrt{5}}$$

     По определению тангенса:

$$tg BOA =\frac{2}{\sqrt{5}}:(-\frac{1}{\sqrt{5}})=-2$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Всего два конца из четырех возможно взять $$C_{m}^{n}=\frac{m!}{(m-n!)}=$$$$C_{4}^{2}=\frac{4}{(4-2)}=6=N$$ способами. По диагонали же $$n=2$$ способами

     Вероятность: $$P=\frac{n}{N}=\frac{2}{6}=0,(3)$$. Округлим до сотых: 0,33

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть $$\angle A=\alpha$$, тогда $$\angle AEB=90-\alpha$$. Но тогда $$\angle CED=\alpha$$, следовательно, треугольники ABE и CED подобны. Из подобия получаем отношение: $$\frac{AB}{BE}=\frac{ED}{CD}$$. Тогда $$CD=\frac{ED*BE}{AB}=\frac{5*8}{4}=10$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Чтобы прямая являлась касательной, тогда производные должны быть одинаковы:
$${y_{1}}'={y_{2}}'\Leftrightarrow$$ $$3=2ax+2\Leftrightarrow$$ $$x=\frac{1}{2a}(1)$$
     С другой стороны, функции тоже должны быть одинаковы:
$$y_{1}=y_{2}\Leftrightarrow$$ $$3x+1=ax^{2}+2x+3 (2)$$

     Подставим (1) в (2):

$$3*\frac{1}{2a}+1=a*(\frac{1}{2a})^{2}+2*\frac{1}{2a}+3\Leftrightarrow$$$$\frac{3}{2a}+1=\frac{a}{4a^{2}}+\frac{2}{2a}+3\Leftrightarrow$$ $$\frac{3}{2a}+1=\frac{1}{4a}+\frac{2}{2a}+3\Leftrightarrow$$$$\frac{3}{2a}-\frac{1}{4a}-\frac{2}{2a}=3-1\Leftrightarrow$$ $$\frac{6-1-4}{4a}=2\Leftrightarrow$$ $$\frac{1}{4a}=2\Leftrightarrow$$ $$a=\frac{1}{8}=0,125$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$AD_{1}^{2}=AH^{2}+HH_{1} ^{2}+H_{1}D_{1}^{2}=$$$$1^{2}+2^{2}+1^{2}=6$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$(b^{2}-49)(\frac{b+1}{b-2}-\frac{b-1}{b+7})-15b+7=$$$$(b^{2}-49)\frac{((b+1)(b+7)-(b-1)(b-7))}{(b-7)(b+7)}-15b+7=$$$$(b^{2}+8b+7-b^{2}+8b-7)-15b+7=$$$$16b-15b+7=b+7=123+7=130$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$F=qvB\ sin \alpha \Leftrightarrow$$ $$\sin \alpha =\frac{F}{qvB}$$

$$\sin\alpha =\frac{3*10^{-8}}{2*10^{-6}*6*5*10^{-3}}=$$$$\frac{10}{2*2*5}=\frac{1}{2}$$

$$\alpha=30$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Пусть x-количество оборотов в минуту первой, y- количество оборотов в минуту второй, тогда если оборот принять за 1:

$$\left\{\begin{matrix}\frac{1}{y}-\frac{1}{x}=\frac{5}{60} \\1*x-1*y=2 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{1}{y}-\frac{1}{x}=\frac{1}{12} \\x=2+y(2)\end{matrix}\right.$$

     Подставим (2) в первое уравнение:

$$\frac{1}{y}-\frac{1}{2+y}=\frac{1}{12}\Leftrightarrow$$ $$12(2+y-y)=2y+y^{2}\Leftrightarrow$$$$y^{2}+2y-24=0$$

$$\left\{\begin{matrix}y_{1}+y_{2}=-2 \\y_{1}*y_{2}=-24 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y_{1}=-6 \\y_{2}=4 \end{matrix}\right.$$

    Отрицательной скорость быть не может, следовательно, второе тело совершает 4 оборота в минуту

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     При x>0: $$\sqrt{4x^{4}=3x^{2}+9}>\sqrt{4x^{4}-8x^{2}+9}$$

     Пусть $$t=\frac{\sqrt{4x^{4}-3x^{2}+9}-\sqrt{4x^{4}-8x^{2}+9}}{x}=$$$$\frac{4x^{4}-3x^{2}+9-(4x^{4}-8x^{2}+9)}{x(\sqrt{4x^{4}-3x^{2}+9}+\sqrt{4x^{4}-8x^{2}+9})}=$$$$\frac{5x^{2}}{\sqrt{4x^{4}-3x^{2}+9}+\sqrt{4x^{4}-8x^{2}+9}}=$$$$\frac{5}{\sqrt{4x^{4}-\frac{9}{x^{2}}-3}+\sqrt{4x^{4}-\frac{9}{x^{2}}-8}}$$

     Учтем, что $$a^{2}+b^{2}\geq 2ab$$. Пусть $$a^{2}=4x^{2}, b^{2}=\frac{9}{x^{2}}$$. Тогда: $$4x^{2}+\frac{9}{x^{2}}\geq 2\sqrt{4x^{2}*\frac{9}{x^{2}}}=2*6=12(1)$$

     Следовательно $$\sqrt{4x^{4}-\frac{9}{x^{2}}-3}+\sqrt{4x^{4}-\frac{9}{x^{2}}-8}(2)$$ минимальна при выполнении (1):

$$\sqrt{12-3}+\sqrt{12-8}=3+2=5$$. Чем меньше (2), тем больше t и тем меньше: $$\log_{0,5}t\Rightarrow \log_{0,5}\frac{5}{5}=\log_{0,5}1=0$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

А)   $$\frac{2+\cos 4x-8\cos^{4}x }{4(\cos x+\sin x)}=\frac{1}{\sin x}$$

     Область определения D: $$\left\{\begin{matrix}\cos x+\sin x \neq 0\\\ \sin x\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}tg x\neq -1\\x\neq \pi n , n \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} x\neq -\frac{\pi}{4}+\pi n\\x\neq \pi n\end{matrix}\right.$$

     Рассмотрим числитель первой дроби:

$$\cos 4x=2 \cos^{2}2x-1=$$$$2(2 \cos ^{2}x-1)^{2}-1=2(4\cos ^{4}x-4\cos ^{2}x+1)=$$$$8\cos^{4}x-8 \cos ^{2}x+1=$$$$3+8\cos^{4}x-8 \cos ^{2}x+1-8\cos ^{4}x=4-8\cos ^{2}x$$

     Выполним преобразования:

$$\frac{4(1-2\cos^{2}x)}{4(\cos x+\sin x)}=\frac{1}{\sin x}\Leftrightarrow$$$$\frac{1-2 \cos ^{2}x}{\cos x+\sin x}=\frac{1}{\sin x}\Leftrightarrow$$$$\sin x-2 \cos^{2}x*\sin x=\cos x+\sin x\Leftrightarrow$$$$\cos x+2 \cos^{2}x \sin x=0\Leftrightarrow$$$$\cos x(1+2\cos x \sin x)=0\Leftrightarrow$$

     Произведение равно нулю, когда хотя бы один из множителей равен нулю: 

$$\left[\begin{matrix}\cos x=0\\1+\sin 2x=0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi}{2}+\pi n\\2x=-\frac{\pi}{2}+2\pi n\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi}{2}+\pi n\\x=-\frac{\pi}{4}+\pi n\notin D\end{matrix}\right.$$

Б)   Найдем корни, принадлежащие данному промежутку: $$\pi\approx 3,14\Rightarrow$$ $$\frac{\pi}{2}\approx 1,57$$. Тогда $$\frac{\pi}{2}+\pi=\frac{3 \pi}{2}\in [2 ;5]$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     (Чтобы построить сечение, нужно будет проводить $$N_{1}O$$ до пересечения с $$BC$$ в точке F, и соединять KF)

A)   1)$$\angle ACB=2 \arcsin \frac{4}{5}\Rightarrow$$ $$\sin \angle ACB =\sin (2 \arcsin \frac{4}{5})=$$$$2\sin (\arcsin \frac{4}{5})\cos(\arcsin \frac{4}{5})=$$$$2\frac{4}{5}-\sqrt{1-(\frac{4}{5})^{2}}=$$$$\frac{8}{5}*\frac{3}{5}=\frac{24}{25}$$. Учитываем, что угол $$\arcsin$$ которого составляет $$\frac{4}{5}$$ больше $$\in (45;90)$$. Следовательно, двойной угол будет $$\in (90;180)$$, то есть его косинус отрицательный: $$\cos \angle ACB=-\sqrt{1-(\frac{24}{25})^{2}}=-\frac{7}{25}$$

     2) $$A_{1}B_{1}=\sqrt{C_{1}A_{1}^{2}+C_{1}B_{1}^{2}-2C_{1}A_{1}*C_{1}B_{1}*\cos A_{1}C_{1}B_{1}}=$$$$\sqrt{2^{2}+2^{2}+2*2^{2}*\frac{7}{25}}=\frac{16}{5}$$

     3) $$AK=\frac{7}{16}AB=\frac{7}{16}*\frac{16}{5}=\frac{7}{5}$$; $$KB=\frac{9}{16}*\frac{16}{5}=\frac{9}{5}$$; $$B_{1}L=\frac{7}{5}$$; $$LA_{1}=\frac{9}{5}$$; $$K_{1}M_{1}=B_{1}M_{1}-LB_{1}=\frac{8}{5}-\frac{7}{5}=\frac{1}{5}=MK$$

$$LM_{1}\left | \right |KM$$ и $$MM_{1}\perp AB A_{1}B_{1}\Rightarrow$$ $$\Delta LM_{1}O_{1}=\Delta O_{1}MK\Rightarrow M_{1}O_{1}=O_{1}K$$, но $$LN_{1}\left | \right |KN\left | \right |OO_{1}\Rightarrow C_{1}O=OC$$

Б)   1) $$O_{1}L\perp N_{1}L$$ т.к. $$M_{1}L\perp N_{1}L$$ (теорема о трех перпендикулярах)

$$B_{1}L=\frac{7}{5}\Rightarrow$$ $$\frac{B_{1}L}{B_{1}M_{1}}=\frac{7}{5}*\frac{5}{8}=\frac{7}{8}\Rightarrow$$ $$N_{1}L=\frac{7}{8}C_{1}M_{1}=\frac{7}{8}OO_{1}\Rightarrow$$ $$S_{OO_{1}LN_{1}}=\frac{OO_{1}+\frac{7}{8}OO_{1}}{2}*O_{1}L=\frac{15}{16}OO_{1}*O_{1}L$$ (так как имеем прямоугольную трапецию)

$$O_{1}L\perp N_{1}L$$ т.к. $$M_{1}L\perp N_{1}L$$ (теорема о трех перпендикулярах)

     2) из $$\Delta LO_{1}A_{1}:$$ $$O_{1}M_{1}=\sqrt{LM_{1}*M_{1}A_{1}}=\sqrt{\frac{1}{5}*\frac{8}{5}}=\frac{2\sqrt{2}}{5}$$

$$K_{1}O_{1}=\sqrt{(\frac{1}{5})^{2}+(\frac{2\sqrt{2}}{5})^{2}}=\sqrt{\frac{1}{25}+\frac{8}{25}}=\frac{3}{5}$$

$$OO_{1}=C_{1}M_{1}=\sqrt{2^{2}-(\frac{8}{5})^{2}}=\sqrt{4-\frac{64}{25}}=\frac{6}{5}$$

     3) Тогда площадь всего сечения есть удвоенная $$S_{OO_{1}LN_{1}}$$: $$S=\frac{15}{16}*\frac{6}{5}*\frac{3}{5}*2=1,35$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\log_{8}(\frac{1}{3}-x)\log_{12x+\frac{1}{3}}(\frac{1}{3}-x)>\log_{2}\frac{(\frac{1}{3}-x)}{\sqrt[3]{(2x+\frac{1}{3})^{2}}}$$

     С учетом того, что $$\sqrt[3]{(2x+\frac{1}{3})^{2}} \geq 0$$ получаем следующую область определения $$D(x)$$:

$$\left\{\begin{matrix}\frac{1}{3}-x>0\\ |2x+\frac{1}{3}|>0\\ |2x+\frac{1}{3}|\neq 1\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x<\frac{1}{3}\\ 2x+\frac{1}{3}\neq 0\\ 2x+\frac{1}{3}\neq 1\\ 2x+\frac{1}{3}\neq -1\end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}x<\frac{1}{3}\\ x\neq -\frac{1}{6}\\ x\neq -\frac{1}{3}\\ x\neq -\frac{2}{3}\end{matrix}\right.$$

     Преобразуем правую часть неравенства: $$\log_{2}\frac{(\frac{1}{3}-x)}{\sqrt[3]{(2x+\frac{1}{3})^{2}}}=$$$$\log_{2}(\frac{1}{3}-x)-\log_{2}\sqrt[3]{(2x+\frac{1}{3})^{2}}=$$$$\log_{2}(\frac{1}{3}-x)-\frac{2}{3}\log_{2}|2x+\frac{1}{3}|$$

     Пусть $$a=\frac{1}{3}-x$$ и $$b=|2x+\frac{1}{3}|$$, тогда:

$$\frac{1}{3}\log_{2}a\log_{b}a-\log_{2}a+\frac{2}{3}\log_{2}b>0\Leftrightarrow$$$$\log_{2}a\log _{b}a(1-\frac{3}{\log_{b}a}+\frac{2 \log_{2}b}{\log_{2}a \log_{b}a})>0\Leftrightarrow$$$$\log_{2}a \log_{b}a(\frac{\log_{b}^{2}a-3\log_{b}a+2}{\log_{b}^{2}a})>0\Leftrightarrow$$$$\frac{\log_{2}a}{\log_{b}a}(\log_{b}^{2}a-3\log_{b}a+2)>0\Leftrightarrow$$$$\frac{\log_{a}b}{\log_{a}2}(\log_{b}a-2)(\log_{b}a-1)>0\Leftrightarrow$$$$\log_{2}b(\log_{b}a-\log_{b}b^{2})(\log_{b}a-\log_{b}b)>0\Leftrightarrow$$

     Воспользуемся методами рационализации для логарифмов:

$$(b-1)(a-b^{2})(b-1)(a-b)(b-1)>0\Leftrightarrow$$$$(b-1)(a-b^{2})(a-b)>0$$

     Вернемся обратно к заменам:

$$(\left | 2x+\frac{1}{3} \right |-1)(\frac{1}{3}-x-(2x+\frac{1}{3})^{2})(\frac{1}{3}-x-\left | 2x+\frac{1}{3} \right |)\Leftrightarrow$$$$(\left | 2x+\frac{1}{3} \right |-1)(36x^{2}+21x-2)(\left | 2x+\frac{1}{3} \right |-\left | \frac{1}{3}-x \right |)>0$$

     С учетом D(f): $$\frac{1}{3}-x>0$$, при всех Х. Тогда $$\frac{1}{3}-x$$ мы можем представить, как $$|\frac{1}{3}-x|$$, а так же $$1=|1|$$ и воспользоваться методами рационализации для модулей:

$$(2x+\frac{1}{3}-1)(2x+\frac{1}{3}+1)(x-\frac{1}{12})(x+\frac{2}{3})(2x+\frac{1}{3}-\frac{1}{3}+x)(2x+\frac{1}{3}+\frac{1}{3}-x)>0\Leftrightarrow$$$$(2x-\frac{2}{3})(2x+\frac{4}{3})(x-\frac{1}{2})(x+\frac{2}{3})(3x)(x+\frac{2}{3})>0\Leftrightarrow$$$$(x+\frac{2}{3})(x-\frac{1}{3})(x-\frac{1}{12})x>0$$

     Получаем, что (промежутки выделены синим цветом): $$\left[\begin{matrix}x< -\frac{2}{3}\\ \left\{\begin{matrix}x> 0\\ x<\frac{1}{2}\end{matrix}\right.\\ x> \frac{1}{3}\end{matrix}\right.$$

     С учетом $$D(x)$$: $$\left[\begin{matrix}x< -\frac{2}{3}\\\left\{\begin{matrix}x>0\\x<\frac{1}{12} \end{matrix}\right.\end{matrix}\right.$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

A)   1) Из $$\Delta ABC$$: $$AC=\sqrt{AB^{2}+BC^{2}-2AB*BC*\cos B}=$$$$\sqrt{9+9-2*5*\frac{1}{9}}=$$$$\sqrt{18-2}=4$$

     2)по свойству биссектрис: $$\frac{AM}{MP}=\frac{AC}{DC}=$$$$\frac{1,5}{4}=\frac{3}{8}\Rightarrow$$ $$MD=\frac{3}{11}AC=\frac{12}{11}$$

     3) Из $$\Delta MDQ\sim \Delta ADC\Rightarrow$$ $$\frac{MD}{AD}=\frac{DQ}{DC}=\frac{3}{11}\Rightarrow$$ $$DQ=\frac{1,5*3}{11}=\frac{9}{22}\Rightarrow$$ $$BQ=1,5+\frac{9}{22}=\frac{3}{2}+\frac{9}{22}=$$$$\frac{33+9}{22}=\frac{42}{22}=\frac{21}{11}$$

     4) Из $$\Delta PBQ\sim \Delta ABC\Rightarrow$$ $$\frac{PQ}{AC}=\frac{BQ}{BC}=$$$$\frac{21}{11}:3=\frac{21}{33}$$. Тогда $$PQ=\frac{21*4}{33}=\frac{84}{33}$$

     5)$$PM=PQ-QM=\frac{84}{33}-\frac{12}{11}=$$$$\frac{84-36}{33}=\frac{48}{33}=\frac{16}{11}$$

Б)   1) $$BP=BQ=\frac{21}{11}$$, $$p=\frac{\frac{21}{11}+\frac{21}{11}+\frac{84}{33}}{2}=$$$$\frac{42+28}{22}=\frac{70}{22}=\frac{35}{11}$$

     2) По формуле Герона: $$r=\frac{S}{p}=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}$$. Тогда: $$r=\sqrt{\frac{(\frac{35}{11}-\frac{21}{11})^{2}(\frac{35}{11}-\frac{28}{11})}{\frac{35}{11}}}=$$$$\sqrt{(\frac{14}{11})^{2}*\frac{7}{11}*\frac{11}{35}}=$$$$\frac{14}{11\sqrt{5}}=\frac{14\sqrt{5}}{55}$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

     Очевидно, что необходимо снимать деньги в тот год, когда увеличение цены на 2000 рублей будет меньше, чем увеличение на 10%, согласно ставке банка. Пусть n - год, в который это произойдет.

     Следует учитывать, что начисление 2000 рублей происходит в конце года, а снять и положить можно только в начале, потому результат мы должны будем увеличить на единицу (например, в конце пятого года цена бумаги позволяет ее перекладывать, то переложим мы только в шестом году).

     Если взять n-ый год, то стоимость бумаги составит: $$7000+2000n$$. Если бы мы ее положили под 10%, то на нее начислилась бы сумма $$0,1(7000+2000n)=700+200n$$. И эта сумма должна быть больше, чем 2000, чтобы был смысл перекладывать деньги в банк:

     $$700+200n>2000\Leftrightarrow$$$$200n>1300|:200\Leftrightarrow$$$$n>6,5$$.

     Так как n - число натуральное, то получаем, что $$n=7$$. То есть в конце 7 года цена бумаги станет такой, что 10% от ее стоимости, составят больше 2000, и тогда на 8 год (2008) мы ее продаем.

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

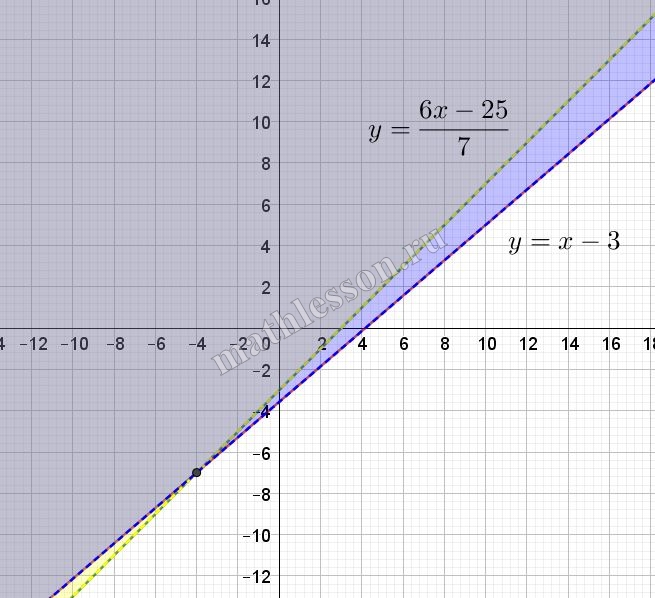
     Рассмотрим область определения данной системы. Так как даны логарифмы, то: $$\left\{\begin{matrix}3-x+y>0\\25-6x+7y>0\end{matrix}\right.\Rightarrow$$ $$\left\{\begin{matrix}y>x-3\\y>\frac{6x-25}{7}\end{matrix}\right.$$ (желтым выделено решение для первого неравенства, синим - для второго, серым - их пересечение)

     Рассмотрим первое уравнение системы:

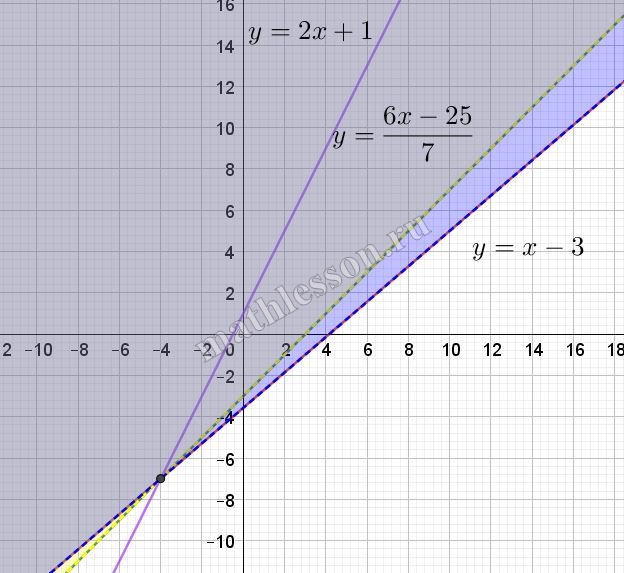
$$\log_{2}(8(3-x+y))=\log_{2}(25-6x+7y)\Leftrightarrow$$$$24-8x+8y=25-6x+7y\Leftrightarrow$$$$y=2x+1 (1)$$

     Построим график данной функции с учетом области определения:

     Как видим, чтобы было два пересечения, x должен быть больше 4 (иначе часть прямой лежит вне области определения)

     Подставим  (1) во второе:$$2+2x+1=(x-2a)^{2}+a+2x\Leftrightarrow$$$$(x-2a)^{2}=3-a$$

     Так как число в квадрате, то правая часть уравнения должна быть больше нуля (если равна нулю, то корень всего один): $$3-a>0\Rightarrow a<3$$

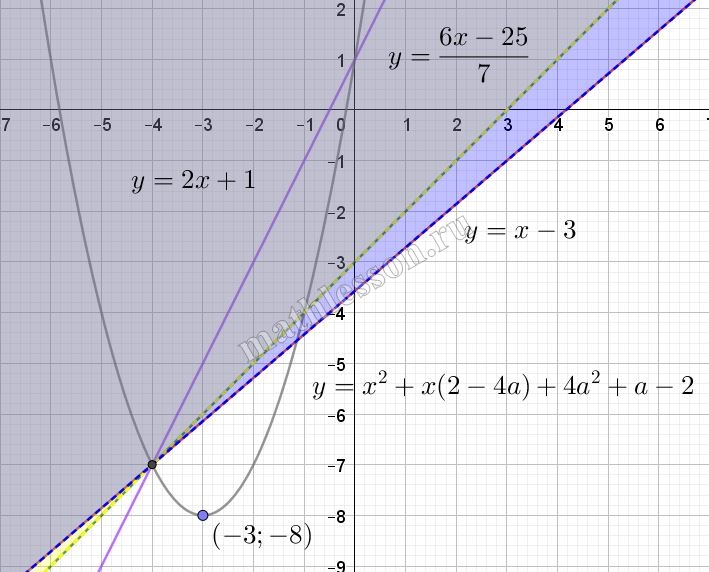
     Рассмотрим график второй функции:

$$y+2=x^{2}-4ax+2a^{2}+a+2x\Leftrightarrow$$$$y=x^{2}+x(2-4a)+4a^{2}+a-2$$

     Найдем вершину параболы:

$$x_{0}=-\frac{2(1-2a)}{2}=2a-1$$

$$y_{0}=4a^{2}-4a+1-2(2a-1)^{2}+4a^{2}+a-2=8a^{2}-3a-1-8a^{2}+8a-2=5a-3$$

     Рассмотрим возможное расположение графика с учетом области определения:

     Как видим, координата y вершины параболы должна быть больше -8, а х больше -3 (если будет левее, то отно пересечение точно не попадет в область определения) :

$$\left\{\begin{matrix}2a-1>-3\\5a-3>-8\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a>-1\\a>-1\end{matrix}\right.$$

     С учетом того, что $$a<3$$, получаем: $$a \in (-1;3)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

А)   Да.Есть два возможных расположения чисел 2 и 11 относительно других чисел. 

• если они идут рядом. Пусть числа идут в порядке возрастания (2,11). Тогда мы всегда сможем начать убывающую последовательно с 11. Из оставшихся 9 чисел в любом случае надется расположение двух, идущих друг за другом, в порядке убывания). Исключение составляет случай, когда все следующие будут расположены в порядке возрастания, но тогда из них мы сможем построить возрастающую последовательность. Аналогичное рассуждение для убывания.
• если между ними есть число. Тогда они в любом случае будут или возрастающей последовательностью (2,а,11) или убывающей (11, а, 2)

Б)   Нет. Достаточно привести пример: 7 5 2 9 6 11 4 10 3 8. (Смысл его построения сводится к тому, что в середину ставится 11, а далее через одно раскидываются больше оставшиеся, а промежутки заполняются меньшими. Подобное расположение не дает построить последовательность, будь то возрастающая или убывающая, более, чем из 4 чисел) 

В)   Да. Рассмотрим уже имеющуюся в пункте (Б) полседовательность. Для каждого числа из нее мы подберем пару чисел (a,b), где а - количество чисел максимально длинной возрастающей последовательности, начинающей с текущего числаб b - убывающей: 7(3,4)  5(3,3)  2(3,1)  9(2,4)  6(2,3)  11(1,3)  4(2,2)  10(1,2)  3(2,1)  8(1,1). Как видим среди встречающихся пар чисел нет повторяющихся. При этом, в пункте (Б) мы доказали, что a,b<5, то есть числа в парах могут быть только 1,2,3,4. Согласно комбинаторике, если $$a,b \in [1;3]$$, то число возможных пара (a,b) составляет $$3*3=9$$. А у нас пар числе 10. Это означает, что однозначно одна пара чисел будет содержать хоть одну 4. Следовательно, будет последовательность из 4 чисел.