265 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 265 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №265 (alexlarin.com)
Решаем ЕГЭ 265 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №265 (alexlarin.com)
Задание 1
Необходимо перевезти 50 скутеров весом 300 килограмм каждый. Сколько рейсов понадобится сделать для этого, используя машину грузоподъемностью 5 тонн?
В одну машину заходит максимум 16 скутеров: 4,8 тоны $$\Rightarrow$$ $$\frac{50}{16}\approx$$ 4 рейса
Задание 2
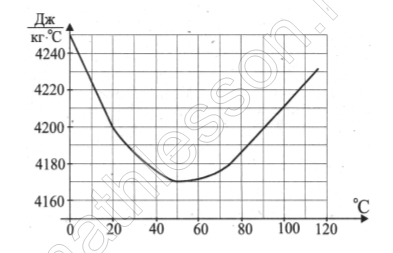
На графике показано изменение удельной теплоёмкости водного раствора некоторого вещества в зависимости от температуры. По горизонтали указывается температура в градусах Цельсия, по вертикали – удельная теплоёмкость в Дж/Кг*0С . Определите по рисунку, на сколько изменится удельная теплоемкость при нагревании раствора с 20° до 100°. Ответ дайте в Дж/Кг*0С .
При 20 градусах: 4200 ; при 100 градусах : 4210 ; Изменение :4210-4200-=10
Задание 3
Радиус большого круга R=2 клетки, малого $$r=\frac{R}{2}\Rightarrow$$ $$S_{1} =\pi (\frac{R}{2})^{2}=\frac{\pi R^{2}}{4}=\frac{S}{4}=4$$, где $$S$$ и $$S_{1}$$ площади большого и малого кругов соответственно , тогда S=4*4=16
Тогда площадь кольца: $$S-S_{1}=12$$. При этом уберем сегмент (его площадь $$\frac{1}{8}$$ от кольца) $$\Rightarrow$$ итоговая площадь $$12*\frac{7}{8} =10,5$$.
Задание 4
В классе учится 16 человек: 6 мальчиков и 10 девочек. Перед началом уроков классный руководитель случайным образом выбирает двух учащихся класса для дежурства в столовой. Какова вероятность, что дежурить в столовую отправятся мальчик с девочкой?
Вероятность выбрать сначала мальчика, потом девочку: $$\frac{6}{16}*\frac{10}{15}=\frac{1}{4}$$
Девочку, потом мальчика: $$\frac{10}{16}*\frac{6}{15}=\frac{1}{4}$$
Следовательно, вероятность, что попадут мальчик и девочка: $$\frac{1}{4}+\frac{1}{4}=0,5$$
Задание 5
Радиус окружности, описанной около правильного шестиугольника, равен $$\sqrt{3}$$ . Найдите радиус вписанной окружности
$$R=\frac{r}{\sin 60}$$, где R-описанной; r –вписанной $$\Rightarrow$$ $$r=R \sin 60 =\sqrt{3} *\frac{\sqrt{3}}{2}=1,5$$
Задание 6
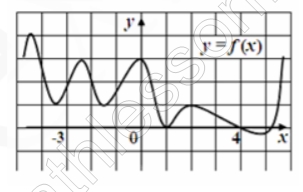
По графику функции у = f(x) определите количество точек на интервале (‐3; 4), в которых касательная к графику параллельна прямой у = 0,3х – 4 или совпадает с ней.
Если параллельна или совпадает , то $$f^{'}=(0,3x-4)^{'}=0,3$$. Тогда точки (отмечены на рисунке) находятся на промежутке возрастания , и их количество 5. (Можно построить схематичный график производной)
Задание 7
Объем правильной шестиугольной призмы равен 180. Сначала каждое ее боковое ребро увеличили в два раза, а затем каждую сторону каждого основания уменьшили в три раза. Найдите объем полученной призмы.
Пусть h –начальная высота $$\Rightarrow$$ $$h_{1}=2h$$, a –сторона основания $$\Rightarrow$$ $$a_{1} =\frac{a}{3}\Rightarrow$$ $$\frac{S}{S_{1}}=(\frac{3}{1})^{2}=\frac{9}{1}$$, где $$a_{1},h$$ и $$S_{1}$$ –сторона , высота и площадь основания новой призмы . $$\Rightarrow$$ $$\frac{V}{V_{1}}=\frac{Sh}{S_{1}h_{1}}=\frac{9}{2}=4,5$$$$\Rightarrow$$ $$V_{1}=\frac{V}{4,5}=40$$
Задание 8
Найдите значение выражения $$\log_{\frac{4}{25}} (\log_{4} 32)$$
$$\log_{\frac{4}{25}}\log_{4}32=$$$$\log_{(\frac{2}{5})^{2}} \log_{2^{2 }}2^{5}=$$$$\frac{1}{2} \log_{\frac{2}{5}}\frac{5}{2} \log_{2} 2=$$$$\frac{1}{2}\log_{\frac{2}{5}}\frac{5}{2}=-0,5$$
Задание 9
Максимальная высота подъёма тела, брошенного под углом к горизонту, вычисляется по формуле $$h=\frac{(v*\sin^{2} \alpha)^{2}}{2g}$$ , где v (м/c) – начальная скорость тела, α – угол, под которым тело брошено к горизонту, g – ускорение свободного падения (считать, что g=10 м/с2). С какой скоростью необходимо бросить мяч под углом 30º к горизонту, чтобы он поднялся на высоту 5 м?
Выразим из формулы скорость: $$h=\frac{(v \sin \alpha )^{2}}{2g}\Leftrightarrow$$ $$2gh=v^{2} \sin ^{2}\alpha \Leftrightarrow$$ $$\frac{2 gh}{\sin ^{2}\alpha }=v^{2}\Leftrightarrow$$ $$v=\frac{\sqrt{2gh}}{\sin \alpha }$$
Найдем скорость : $$v=\frac{\sqrt{2*10*5}}{\sin 30}=\frac{10}{\frac{1}{2}}=20$$
Задание 10
Сцепленные зубчатые колеса вместе в сумме делают 240 оборотов в минуту. Найдите количество зубьев у второго колеса, если у первого их 100, и делает оно на 80 оборотов в минуту больше, чем второе колесо.
Пусть x-количество оборотов второго колеса, тогда $$x+80$$ - первого и $$x+x+80=240\Leftrightarrow$$ $$2x=160$$$$\Leftrightarrow$$ $$x=80$$ - второе колесо, 160-первое.
Первое колесо за 160 оборотов пройдет $$160*100=16000$$ зубьев. Второе пройдет столько же, но за 80 оборотов, следовательно , у него $$\frac{16000}{80}=200$$ зубьев.
Задание 11
Найдите наибольшее значение функции $$y=(x-1)*2^{x}$$ на отрезке [2; 6]
1) Найдем производную функции и приравняем к 0 : $$y^{'}=(x-1)^{'}2^{x}+(x-1)(2^{x})^{'}=2^{x}+(x-1)2^{x}\ln 2=0\Leftrightarrow$$$$2^{x}(1+(x-1)\ln 2)=0\Leftrightarrow$$ $$1+(x-1)\ln 2=0\Leftrightarrow$$ $$x-1=\frac{-1}{\ln 2}\Leftrightarrow$$ $$x=-\frac{1}{\ln 2}-1=-\log_{2}e-1=$$$$\log_{2}\frac{1}{e}-1=$$$$\log_{2}\frac{1}{2e}<0\Rightarrow$$ на промежутке [2 ;6] $$y_{max}=y(6)=(6-1)2^{6}=320$$
2) Можно решить рассуждением:
На промежутке [2; 6] : y=(x-1) и возрастает $$y=2^{x} \Rightarrow$$ $$y=(x-1)2^{x}\Rightarrow$$ $$y_{max}=y(6)$$
Задание 12
A) $$3*2^{\cos x+3\sqrt{1-\sin ^{2}x}}+11 *2^{2 \cos x}-34=0\Leftrightarrow$$ $$3*2^{\cos x+3\sqrt{\cos ^{2}x}}+11*2^{2 \cos x}-34=0\Leftrightarrow$$ $$3*2^{\cos x+3\left | \cos ^{2}x \right |}+11*2^{2 \cos x}-34=0$$
1) при $$\cos x\geq 0$$$$\Leftrightarrow$$ $$x \in [-\frac{\pi}{2}+2 \pi n, \frac{\pi}{2}+2 \pi n], n \in Z$$: $$3*2^{4 \cos x}+11*2^{2 \cos x}-34=0$$
Пусть $$2^{2 \cos x}=y>0$$, тогда $$3y^{2}+11y-34=0$$: $$D=121+408=529$$
$$\left[\begin{matrix}y_{1}=\frac{-11+23}{6}=2\\y_{2}=\frac{-11-23}{6}<0\end{matrix}\right.\Leftrightarrow$$ $$2 ^{2 \cos x}=2\Leftrightarrow$$ $$2 \cos x=1\Leftrightarrow$$ $$\cos x=\frac{1}{2}\Leftrightarrow$$ $$x=\pm \frac{\pi}{3}+2 \pi n , n \in Z$$
2) при $$\cos x<0$$: $$3*2^{\cos x-3 \cos x}+11*2^{2 \cos x}-34=0\Leftrightarrow$$$$3*2^{-2\cos x}+11*2^{2 \cos x}-34=0$$
Пусть $$2^{2 \cos x}=y>0$$ , тогда $$\frac{3}{y}+11*y-34=0\Leftrightarrow$$ $$\frac{11y^{2}-34y+3}{y}=0\Leftrightarrow$$ $$11y^{2}-34y+3=0$$
$$D=1156-132=1024$$
$$\left[\begin{matrix}y_{1}=\frac{34+32}{22}=3\\y_{2}=\frac{34-32}{22}=\frac{1}{11}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}2^{2 \cos x}=3\\2 ^{2 \cos x}=\frac{1}{11}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}4^{\cos x}=3\\4^{\cos x}=\frac{1}{11}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\cos x=\log_{4}3>0\Rightarrow \varnothing\\\cos x=\log_{4}\frac{1}{11}<-1\Rightarrow \varnothing & &\end{matrix}\right.$$
Б) На промежутке $$[-\frac{\pi}{2};\frac{5\pi}{2}]$$:
$$\frac{\pi}{3}+2 \pi n$$: $$\frac{\pi}{3};\frac{7\pi}{3}$$
$$-\frac{\pi}{3}+2 \pi n$$: $$\frac{\pi}{3};\frac{5\pi}{3}$$
Задание 13
В основании пирамиды с вершиной S лежит прямоугольник, центр которого находится на высоте пирамиды. Плоскость пересекает боковые ребра пирамиды в точках P, Q, M и N так, что Р и М – противоположные вершины четырехугольника PQMN. Известно, что $$SP=7$$, $$SM=\frac{7}{6}$$, $$SQ+SN=\frac{25}{6}$$, $$SQ>SN$$
A) 1)Через P проведем плоскость параллельную (ABC): $$PQ_{1}M_{1}N{1})$$$$\Rightarrow$$ $$SP=SQ=SM_{1}=SN_{1}=7$$. Пусть H –центр ABCD $$\Rightarrow$$ SH –высота пирамиды; $$SH\cap (PQMN)=O$$, $$SH\cap (PQ_{1}M_{1}N_{1})=O_{1}$$ ; $$MM_{1}=SM_{1}-SM=\frac{35}{6}$$
2) Из $$\Delta SM_{1}P$$: $$M_{1}Q_{1}=O_{1}P\Rightarrow$$ по т. Менелая для $$\Delta MPM_{1}$$ : $$\frac{SO}{OO_{1}}*\frac{O_{1}P}{PM_{1}}*\frac{M_{1}M}{MS}=1\Leftrightarrow$$ $$\frac{SO}{OO_{1}}*\frac{1}{2}*\frac{35}{6}:\frac{7}{6}=1\Leftrightarrow$$ $$\frac{SO}{OO_{1}}=\frac{2}{5}$$
3) Рассмотрим $$\Delta SQ_{1}N_{1}$$: пусть $$SQ=x\Rightarrow$$ $$SN=\frac{25-x}{6}$$; Построим $$N_{2}Q_{2}\left | \right |N_{1}Q_{1}\Rightarrow$$ $$\Delta SON_{2}\sim \Delta SO_{1}N_{1}\Rightarrow$$ $$\frac{SN_{2}}{N_{2}N_{1}}=\frac{SO}{OO_{1}}=\frac{2}{5}$$. Т.е. $$SN_{1}=7$$, то $$SN_{2}=2=SQ_{2}$$, тогда $$N_{2}N=SN_{2}-SN=2-(\frac{25}{6}-x)=x-\frac{13}{6}$$; $$Q_{2}Q=SQ-SQ_{2}=x-2$$
По т. Менелая для $$\Delta NSQ$$: $$\frac{N_{2}O}{OQ_{2}}*\frac{Q_{2}Q}{QS}*\frac{SN}{NN_{2}}=1$$$$\Leftrightarrow$$ $$\frac{1}{1}*\frac{x-2}{x}*\frac{\frac{25}{6}-x}{x-\frac{13}{6}}=1$$$$\Leftrightarrow$$ $$(x-2)(\frac{25}{6}-x)=x(x-\frac{13}{6})|*6$$$$\Leftrightarrow$$ $$12x^{2}-50x+50=0\Leftrightarrow$$ $$6x^{2}-25x+25=0\Leftrightarrow$$ $$\left[\begin{matrix}x_{1}=\frac{5}{2}\\x_{2}=\frac{5}{3}\end{matrix}\right.$$
$$\frac{5}{3}$$ не подходит, т.к. $$\frac{25}{6}-\frac{5}{3}=\frac{5}{2}$$ и $$\frac{5}{3}<\frac{5}{2}$$, а по условию $$SQ>SN\Rightarrow$$ $$SQ=\frac{5}{2}$$; $$SN=\frac{5}{3}$$
Б) 1) Рассмотрим $$\Delta SHD$$: $$SQ_{2}=2$$; $$Q_{2}Q_{1}=5$$; $$Q_{1}D=SD-SQ_{1}=10-7=3\Rightarrow$$ $$Q_{2}D=5+3=8$$
2) $$\Delta SOQ_{2}\sim \Delta SHD\Rightarrow$$ $$\frac{SO}{OH}=\frac{SQ_{2}}{Q_{2}D}=\frac{2}{8}=\frac{1}{4}$$
Задание 14
Решите неравенство $$(\log_{3+x} (1-2x))(\log_{1-2x} x^{2})\leq (\log_{3+x} (1-3x))(\log_{1-3x} (2-x))$$
$$(\log_{3+x}(1-2x))(\log_{1-2x}x^{2})\leq (\log_{3+x}(1-3x))(\log_{1-3x}(2-x))$$
ОДЗ: $$\left\{\begin{matrix}1-2x>0\\3+x>0\\3+x\neq 1\\1-2x\neq 1\\x^{2}>0\\1-3x>0\\2-x>0\\1-3x\neq 1\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}x<0,5\\x>-3\\x\neq -2\\x\neq 0\\x<\frac{1}{3}\\x<2\end{matrix}\right.$$$$\Leftrightarrow$$ $$x \in (-3; -2)\cup (-2; 0)\cup (0; \frac{1}{3})$$
Решение: $$\frac{1}{\log_{1-2x}(3+x)}*\log_{1-2x}x^{2}\leq \frac{1}{\log_{1-3x}(3+x)}*\log_{1-3x}(2-x)\Leftrightarrow$$ $$\log_{3+x}x^{2}\leq \log_{3+x}(2-x)\Leftrightarrow$$ $$(3+x-1)(x^{2}-2+x)\leq 0\Leftrightarrow$$ $$(x+2)(x+2)(x-1)\leq 0\Leftrightarrow$$ $$\left[\begin{matrix}x+2=0\\x\leq 1\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=-2\\x\leq 1\end{matrix}\right.$$
С учетом ОДЗ: $$x \in (-3; -2) \cup (-2; 0)\cup (0; \frac{1}{3})$$
Задание 15
A) 1) $$\angle KBL=\angle ADL=45$$ (угол между диагональю и стороной квадрата);
$$\angle HBT=\angle TDA$$ (накрест лежащие )$$\Rightarrow$$ $$\angle KBT=\angle TDL$$;
$$\angle BTK=\angle LTD$$ (вертикальные )$$\Rightarrow$$ $$\Delta KBT\sim \Delta TDL$$$$\Rightarrow$$ $$\angle BKT=\angle TLD$$
2) из $$\angle KBT=\angle NDL\Rightarrow$$ $$BK\left | \right |LD$$ $$\Rightarrow$$ $$\angle BKT=\angle TLD$$, то они накрест лежащие $$\Rightarrow$$ $$KT\left | \right |TL$$ или $$K,T,L \in KL$$, но параллельны быть не могут (так как имеют общую точку) $$\Rightarrow$$ KL-секущая
Б) 1) Аналогично п. A $$\Delta RCT \sim TAN$$ ($$\angle C=90$$; $$\angle BCD=\angle TAD$$ - накрест лежащие )$$\Rightarrow$$ $$AN\left | \right |RC$$; $$\angle TNA=\angle TRC$$$$\Rightarrow$$ $$R,T,N \in RN$$
2) из подобия : $$\frac{AN}{RC}=\frac{NT}{TR}\Leftrightarrow$$ $$\frac{8}{3}=\frac{20}{x}\Rightarrow$$ $$x=\frac{3*20}{8}=7,5\Rightarrow$$ $$RN=27,5$$
Задание 16
В июле планируется взять кредит в банке на сумму 12 млн. рублей на 15 лет. Условия его возврата таковы:
Какую сумму нужно вернуть банку?
Пусть $$S=12*10^{6}$$ руб. –первоначальная сумма кредита, $$n=15$$ лет-срок кредита, $$a=12$$ % , $$b=4$$ % . Составим таблицу платежей (каждый платеж состоит из суммы по основному долгу $$\frac{S}{15}$$ (за 15 лет надо отдать S) и начисленные за год процентов) :
| № года | Долг на начало года | Сумма по начисленному проценту | Итоговый платеж (по основному долгу и проценту) |
| 1 | $$S$$ | $$\frac{Sa}{100}$$ | $$\frac{S}{15}$$+$$\frac{Sa}{100}$$ |
| 2 | $$\frac{14S}{15}$$ | $$\frac{14S}{15}*\frac{a}{100}$$ | $$\frac{S}{15}$$+$$\frac{14Sa}{1500}$$ |
| ... | ... | ... | ... |
| 8 | $$\frac{8S}{15}$$ | $$\frac{8S}{15}*\frac{a}{100}$$ | $$\frac{S}{15}$$+$$\frac{8Sa}{1500}$$ |
| 9 | $$\frac{7S}{15}$$ | $$\frac{7S}{15}*\frac{b}{100}$$ | $$\frac{S}{15}$$+$$\frac{7Sb}{1500}$$ |
| ... | ... | ... | ... |
| 15 | $$\frac{S}{15}$$ | $$\frac{S}{15}*\frac{b}{100}$$ | $$\frac{S}{15}$$+$$\frac{Sb}{1500}$$ |
Итого будет выплачено : $$\frac{S}{15}*15+\frac{Sa}{100}(1+\frac{14}{15}+..+\frac{8}{15})+\frac{8b}{100}(\frac{7}{15}+\frac{6}{15}+..+\frac{1}{15})$$
Подставим известные значения: $$S+Sa*\frac{92}{15}+8b*\frac{28}{15}=$$$$S(1+\frac{92a}{15}+\frac{28b}{15})=$$$$12*10^{6}(1+\frac{91*12}{15*100}+\frac{28*4}{15*100})=21728000$$
Задание 17
Найдите все значения параметра а, при которых уравнение $$(\cos x -1)^{2}=a(\cos x+4\sin^{2} x-8)$$ имеет на промежутке $$(0;\frac{\pi}{2}]$$ единственный корень.
$$(\cos x-1)^{2}=a(3 \cos x+4 \sin ^{2}x-8)\Leftrightarrow$$ $$(\cos x-1)^{2}=a(3 \cos x+4-4\cos^{2}x-8)\Leftrightarrow$$ $$(\cos x-1)^{2}=a(3\cos x-4 \cos ^{2}x-4)$$
Рассмотрим правую часть : -$$4 \cos^{2}x-4 \in [-8 ;-4]$$ $$(\cos ^{2}x \in [0 ;1] )\Rightarrow$$ $$3 \cos x-4 \cos ^{2}x-4\leq -1$$ при любом x) , при этом $$(\cos x-1)^{2}\geq 0\Rightarrow$$ чтобы выполнялось решение должно быть $$a<0$$ (при a=0 получим, что $$\cos x-1=0 \Rightarrow$$ $$\cos x=1\Rightarrow$$ $$x=2 \pi n \notin (0 \frac{\pi}{2}]$$)
При этом, чтобы было решение на $$(0 ;\frac{\pi}{2}]$$, то $$\cos x \in [0; 1)$$
Сделаем замену $$\cos x=t \in [-1; 1]$$: $$(t-1)^{2}=a(3t-4t^{2}-4)\Leftrightarrow$$ $$\frac{(t-1)^{2}}{a}=-4t^{2}+3t-4$$
Рассмотрим функции : $$f_{1}(t)=\frac{(t-1)^{2}}{a}$$ и $$f_{2}(t)=4t^{2}+3t-4p$$
- $$f_{2}(t): t_{0}=-\frac{3}{-8}=\frac{3}{8}\Rightarrow$$ $$f_{2}(t_{0})=-\frac{55}{16}$$ - парабола, ветви вниз, вершина $$(\frac{3}{8};-\frac{55}{16})$$, сужение к оси симметрии
- $$f_{1}(t)$$: парабола, вершина (1; 0) , ветви в зависимости от a ($$a<0 \Rightarrow$$ вниз )
При этом необходимо единственное решение на $$x \in (0 ;\frac{\pi}{2}]\Rightarrow$$ $$\cos x \in [0; 1) \Rightarrow$$ $$t \in [0; 1)$$ -единственное решение на данном промежутке.
Решение такое будет при $$f_{1}(0)\leq -4$$ $$\Rightarrow$$ $$\frac{(01)^{2}}{a}\leq -4\Rightarrow$$ $$\frac{1}{a}\leq -4\Leftrightarrow$$ $$\frac{1+4a}{a}\leq 0\Rightarrow$$ $$a\in [-\frac{1}{4};0)$$
Задание 18
Пусть $$n=100a+10b+c$$, где $$a \in [1; 9]\in N, b,c \in [0; 9]\in Z$$
A) $$\frac{a^{2}+b^{2}+c^{2}}{100a+10b+c}>1\Rightarrow$$ $$a^{2}+b^{2}+c^{2}>100a+10b+c\Rightarrow$$ $$a^{2}-100a+b^{2}-10b+c^{2}-c>0\Leftrightarrow$$ $$(a-50)^{2}-2500+(b-5)^{2}-25+(c-\frac{1}{2})^{2}-0,25>0\Leftrightarrow$$ $$(a-50)^{2}+(b-5)^{2}+(c-\frac{1}{2})^{2}>2525,25$$
$$(a-50)^{2}=(1-50)^{2}=49^{2}=2401$$. При этом $$max(b-5)^{2}=max(0-5)^{2}=25$$; $$max(c-\frac{1}{2})^{2}=72,25$$. При этом сумма этих максимальных значений : $$2401+25+72,25=2498,25$$, что меньше , чем $$2525,25$$ $$\Rightarrow$$ не может
Б) Аналогично п.А : может , например 199: $$\frac{1^{2}+9^{2}+9^{2}}{199}>\frac{1}{2}\Leftrightarrow$$ $$\frac{163}{199}>\frac{1}{2}$$
B) Рассмотрим $$\frac{a^{2}+b^{2}+c^{2}}{100a+10b+c}\rightarrow max$$. Очевидно , что a=1 (иначе в знаменателе прибавится сотня),а c=9 $$\Rightarrow$$ $$\frac{^{2}+b^{2}+9^{2}}{100+10b+9}=\frac{82+b^{2}}{109+10b}\rightarrow max$$
Найдем производную: $$\frac{(82+b^{2})^{'}(109+10b)-(109+10b)^{'}(82+b^{2})}{(109+10b)^{2}}=$$$$\frac{2b(109+10b)-10(82+b^{2})}{(109+10b)^{2}}=$$$$\frac{10b^{2}+218b-820}{(109+10b)^{2}}=0\Leftrightarrow$$ $$5b^{2}+114b-410=0$$: $$D=20081\approx 141\Rightarrow$$ $$b_{1}=\frac{-114+141}{2*5}=2,7$$; $$b_{2}=\frac{-114-141}{10}=-25,5\rightarrow$$ 2,7-точка минимума $$\Rightarrow$$ $$\frac{82+b^{2}}{109+10b}\rightarrow$$ $$max$$ при $$b=0$$ или при $$b=9$$:
- $$b=0$$: $$\frac{82+0^{2}}{109+10*0}=\frac{82}{109}$$;
- $$b=9$$ :$$\frac{82+9^{2}}{109+10*9}=\frac{163}{199}$$;
$$\frac{163}{199}>\frac{82}{109}\Rightarrow$$ максимальное значение $$\frac{163}{199}$$