262 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 262 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №262 (alexlarin.com)
Решаем ЕГЭ 262 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №262 (alexlarin.com)
Задание 1
В магазине «Сделай сам» мебель продается в разобранном виде. Если покупателю необходимо, он может купить собранную мебель, но в таком случае он должен оплатить сборку, которая составляет 15% от стоимости покупки. Сколько стоит собранный кухонный шкаф, если без сборки он продается за 3200 руб.?
Пусть x руб. – стоимость собранно шкафа, тогда :
$$x=\frac{3200*115}{100}=3680$$ рублей.
Задание 2
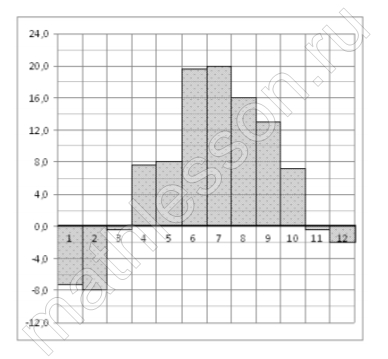
На диаграмме показана среднемесячная температура воздуха в Санкт‐Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной среднемесячной температурой.
Отрицательная была : январь, февраль , март, ноябрь, декабрь - 5 месяцев .
Задание 3
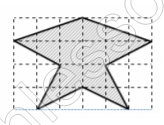
Разобьем данною фигуру на несколько других:
Тогда площадь данной составляет сумму площадей найденных: $$S=S_{1}+S_{2}+S_{3}=3+4+4=11$$
Задание 4
На чашке с ампицилином в среднем из 100 бактерий 1–го вида выживает 20, а из 100 бактерий 2‐го вида выживает 5. Какова вероятность выживания бактерии в условиях этого эксперимента, если соотношение бактерий 1‐го и 2‐го видов в посеве 1:2?
Пусть x-кол-во первого вида, тогда 2x-второго вида. Выживут из первого : $$\frac{20}{100}x=0,2x$$. Из второго: $$\frac{5}{100}*2x=0,1x$$. Всего бактерий: $$2+2x=3x$$. Всего выживут: $$0,2+0,1x=0,3x$$. Вероятность выживания: $$P=\frac{0,3x}{3x}=0,1$$
Задание 5
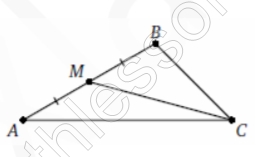
В треугольнике ABC, в котором $$\angle A=30^{\circ}, \angle B=105^{\circ}$$ проведена медиана CM. Найдите $$\angle MCA$$. Ответ дайте в градусах.
- $$\angle C=180-\angle A-\angle B=45$$
- Пусть BN – высота $$\Rightarrow$$ из $$\Delta ABN$$: $$\angle ABN=60\Rightarrow$$ $$\angle NBC=45$$ $$\Rightarrow$$ из $$\Delta BNC$$: $$\angle NCB=45$$ $$\Rightarrow$$ $$BN=NC=\alpha$$
- из $$\Delta ABN$$: $$AB=\frac{BN}{\sin 30}=\frac{x}{\frac{1}{2}}=2x\Rightarrow$$ $$NM=\frac{AB}{2}=x$$ (медиана в прямоугольном треугольнике)
- из $$\Delta MBN$$: $$\angle MNB =60\Rightarrow$$ $$\angle MNC=60+90=150\Rightarrow$$ $$\angle MCA=\frac{180-150}{2}=15$$
Задание 6
Прямая, параллельная оси абсцисс, касается графика функции $$f(x)=-2x^{2}+6x-7$$ . Найдите ординату точки касания.
Пусть y=a - прямая, параллельная Ox $$\Rightarrow$$ $${y}'=0$$. Раз касается f(x) , то и $${f}'(x)=0$$ ( в точке касания ): $$-4x+6=0 \Rightarrow$$ $$x=1,5$$. Найдем ординату точки касания: $$f(1,5)=-2*1,5^{2}+6*1,5-7=-2,5$$
Задание 7
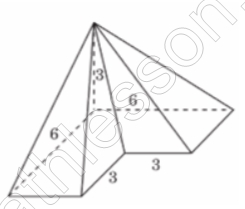
Найдите объём пирамиды, изображённой на рисунке. Её основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых рёбер перпендикулярно плоскости основания и равно 3.
Найдем объем пирамиды без учета выреза: $$V_{1}=\frac{1}{3}*6*6*3=36$$
Найдем объем вырезанной: $$V_{2}=\frac{1}{3}*3*3*3=9$$
Найдем объем оставшейся: $$V=V_{1}-V_{2}=27$$
Задание 8
Найдите значение выражения $$\frac{(\sqrt[7]{8}*\sqrt[3]{81})^{21}}{18^{12}}$$
$$\frac{(\sqrt[7]{8}*\sqrt[3]{81})^{21}}{18^{12}}=$$$$\frac{(8^{\frac{1}{7}}*81^{\frac{1}{3}})^{21}}{(2*3^{2})^{12}}=$$$$\frac{8^{3}*81^{7}}{2^{12}*3^{24}}=$$$$\frac{((2^{3})^{3})*(3^{4})^{7}}{2^{12}*3^{24}}=$$$$\frac{2^{9}*3^{28}}{2^{12}*3^{24}}=\frac{3^{4}}{2^{3}}=10,125$$
Задание 9
В дне цилиндрического бака имеется кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в сантиметрах, меняется по закону $$H(t)=at^{2}+bt+c$$ , где $$a=0,6$$ см/мин2, b (см/мин)– постоянные параметры, t – время в минутах, прошедшее с момента открытия крана. Известно, что через 10 минут после открытия крана вся воды вытечет из бака. Каким будет уровень воды в баке через 6 минут после открытия крана? Ответ выразите в см.
Найдем b : $$H(10)=0=0,6*10^{2}+b*10+96\Leftrightarrow$$ $$60+10b+96=0\Leftrightarrow$$ $$b=15,6$$
Тогда через 6 минут: $$H(6)=0,6*6^{2}-15,6*6+96=117,6-93,6=24$$
Задание 10
Товарный поезд каждую минуту проезжает на 500 метров меньше, чем скорый, и на путь в 120 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
За минуту на 500м =0,5 км. , следовательно, за час: 0,5*60=30км. Пусть x км\ч – скорость товарного, тогда x+30 км\ч – скорость скорого. $$\frac{120}{x}$$ - время товарного , $$\frac{120}{x+30}$$ – время скорого.
$$\frac{120}{x}-\frac{120}{x+30}=2\Leftrightarrow$$ $$\frac{60}{x}-\frac{60}{x+30}=1\Leftrightarrow$$$$60x+1800-60x=x^{2}+30x\Leftrightarrow$$ $$x^{2}+30x-1800=0$$
$$\left\{\begin{matrix}x_{1}+x_{2}=-30\\x_{1}*x_{2}=-1800\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x_{1}=-60\\x_{2}=30\end{matrix}\right.$$.
Скорость не может быть отрицательной $$\Rightarrow$$ 30 км/ч
Задание 11
Найдите точку максимума функции $$y=x^{2}e^{x}$$
$$y=x^{2}*e^{x}\Rightarrow$$ $${y}'={(x^{2})}'e^{x}+{e^{x}}'*x^{2}=$$$$2xe^{x}+e^{x}*x^{2}\Leftrightarrow$$ $$e^{x}(2x+x^{2})=0$$
Т.к. $$e^{x}>0$$ при любом x $$\Rightarrow$$ $$x(2+x)=0\Leftrightarrow$$ $$\left\{\begin{matrix}x=0 \rightarrow min\\x=-2\rightarrow max\end{matrix}\right.$$
Задание 12
А) ОДЗ: $$\sin x\neq 0 \Leftrightarrow$$ $$x\neq \pi n , n \in Z$$
$$\sqrt{7} \cos x(\sqrt{3} ctg x-1-\frac{1}{\sin x})=0\Leftrightarrow$$$$\left\{\begin{matrix}\cos x=0(1)\\\sqrt{3} ctg x-1-\frac{1}{\sin x}=0 (2)\end{matrix}\right.$$
1) $$\cos x=0\Leftrightarrow$$ $$x=\frac{\pi }{2}+\pi n , n \in Z$$
2) $$\frac{\sqrt{3}\cos x}{\sin x}-\frac{1}{\sin x}-1=0\Leftrightarrow$$ $$\frac{\sqrt{3 } \cos x-\sin x-1}{\sin x}=0\Leftrightarrow$$ $$\sqrt{3} \cos x-\sin x=1 \Leftrightarrow$$ $$\frac{\sqrt{3}}{2} \cos x-\frac{1}{2}\sin x=\frac{1}{2}\Leftrightarrow$$ $$\sin \frac{\pi}{3} \cos x-\cos \frac{\pi}{3}\sin x=\frac{1}{2}\Leftrightarrow$$ $$\sin x \cos \frac{\pi}{3}-\cos x \sin \frac{\pi}{3}=-\frac{1}{2}\Leftrightarrow$$ $$\sin (x-\frac{\pi}{3})=-\frac{1}{2}\Leftrightarrow$$ $$\left[\begin{matrix}x-\frac{\pi}{3}=-\frac{\pi}{6}+2 \pi k , k \in Z\\x-\frac{\pi}{3}=-\frac{5 \pi}{6}+2 \pi k\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi}{6}+2 \pi k\\x=-\frac{\pi}{2}+2 \pi k , k \in Z\end{matrix}\right.$$
Б) На промежутке $$[-\pi;\pi]$$:
Задание 13
Основанием пирамиды SABC является правильный треугольник, длина стороны которого равна $$\sqrt{3}$$. Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника АВС. Расстояние от точки О до стороны АС равно 1. Синус угла ОВА относится к синусу угла ОВС как 2:1. Площадь грани SAB равна $$\sqrt{\frac{5}{6}}$$.
A) 1) Пусть $$OL \perp CB$$; $$OM\perp AB$$; $$OK\perp AC$$ .
Из $$\Delta MOB$$: $$\sin \angle OBA=\frac{OM}{OB}$$
Из $$\Delta OLB$$: $$\sin \angle OBL =\frac{OL}{OB}$$
По условию $$\frac{\sin \angle OBA}{\sin \angle OBL}=2\Rightarrow$$ $$OM=2OL$$. Пусть $$OM=2x\Rightarrow$$ $$OL=x$$
2) $$S_{ABC}=S_{AOB}+S_{AOC}+S_{COB}\Leftrightarrow$$ $$\frac{1}{2} AC^{2} \sin 60=\frac{1}{2} AB(OM+OL+OK)\Leftrightarrow$$ $$\sqrt{3} \frac{\sqrt{3}}{2}=1+x+2x\Leftrightarrow$$ $$3x=\frac{1}{2}\Leftrightarrow$$ $$x=\frac{1}{6}\Rightarrow$$ $$OM=\frac{1}{3}; OL=\frac{1}{6}$$
3) $$S_{ABS}=\frac{\sqrt{5}}{\sqrt{6}}=\frac{1}{2}AB*SM$$ ($$OM\perp AB$$; $$SO\perp (ABC)$$$$\Rightarrow$$ $$AM\perp AB$$), тогда : $$SM=\frac{\sqrt{5}}{\sqrt{6}}*\frac{2}{1}*\frac{1}{\sqrt{3}}=\frac{\sqrt{10}}{3}$$
4) из $$\Delta MOS$$: $$SO=\sqrt{SM^{2}-OM^{2}}=1$$
5) $$V_{ABC}=\frac{1}{3} S_{ABC}*SO=$$$$\frac{1}{3}*\frac{3\sqrt{3}}{4}*1=\frac{\sqrt{3}}{4}$$
Б) 1) Аналогично (3): $$SL\perp CB$$. Пусть $$ON\perp SL\Rightarrow$$ $$ON$$ – расстояние от O до (SBC). Пусть $$AL_{1}\left | \right |AL$$ и $$AN_{1}$$ - расстояние от A до (SBC) , тогда $$\Delta AL_{1}N_{1}\sim \Delta OLN$$ и $$\frac{AN_{1}}{ON}=\frac{AL_{1}}{OL}$$
2) из $$\Delta OSL$$: $$SL=\sqrt{OS^{2}+OL^{2}}=\frac{\sqrt{37}}{6}$$; $$ON=\frac{OS*OL}{SL}=\frac{1}{\sqrt{37}}$$
3) из $$\Delta ABC$$ : $$AL_{1} =AB \sin 60=\frac{3}{2}\Rightarrow$$ $$AN_{1} :\frac{1}{\sqrt{37}}=\frac{3}{2}:\frac{1}{6}\Rightarrow$$ $$AN_{1}=\frac{9}{\sqrt{37}}$$
Задание 14
Решите неравенство $$\log_{(x+1)^{2}}8+3\log_{4}(x+1)\geq \frac{37}{4}$$
ОДЗ: $$\left\{\begin{matrix}(x+1)^{2}>0\\(x+1)^{2}\neq 1\\x+1>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x+1\neq 0\\x+1\neq 1\\x\neq 1=-1\\x>-1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq -1\\x\neq 0\\x\neq -2\\x>-1\end{matrix}\right.\Leftrightarrow$$$$x \in (-1; 0)\cup (0; +\infty )$$
Решение: $$\log_{(x+1)^{2}}2^{3}+3\log_{2^{2}}(x+1)\geq \frac{37}{4}\Leftrightarrow$$$$\frac{3}{2}\log_{\left | x+1 \right |}2+\frac{3}{2}\log_{2}(x+1)\geq \frac{37}{4}$$
С учетом, что $$x+1>0$$: $$\left | x+1 \right |=x+1$$: $$\frac{1}{\log_{2}(x+1)}+\log_{2}(x+1)\geq \frac{37}{6}$$
Пусть $$\log_{2}(x+1)=y$$: $$\frac{1}{y}+y-\frac{37}{6}\geq 0\Leftrightarrow$$ $$\frac{6y^{2}-37y+6}{y}\geq 0\Leftrightarrow$$ $$\frac{6(y-6)(y-\frac{1}{6})}{y}\geq 0$$
$$\left[\begin{matrix}\left\{\begin{matrix}y>0\\x\leq \frac{1}{6}\end{matrix}\right.\\y\geq 6\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}\log_{2}(x+1)>0\\\log_{2}(x+1)\leq \frac{1}{6}\end{matrix}\right.\\\log_{2}(x+1)\geq 6\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}x+1>1\\x+1\leq \sqrt[6]{2}\end{matrix}\right.\\x+1\geq 64\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}x>0\\x\leq \sqrt[6]{2}-1\end{matrix}\right.\\x\geq 63\end{matrix}\right.$$
С учетом ОДЗ: $$x \in (0; \sqrt[6]{2}-1]\cup [63; +\infty )$$
Задание 15
Окружность, вписанная в равнобедренный треугольник АВС, касается основания АС в точке D и боковой стороны АВ в точке Е. Точка F – середина стороны АВ, а точка G – точка пересечения окружности и отрезка FD, отличная от D. Касательная к окружности, проходящая через точку G, пересекает сторону АВ в точке Н. Известно, что FH:HE=2:3.
А) 1) $$\angle HGE$$ - угол между хордой EG и касательной HG$$\Rightarrow$$ $$\angle HGE=\frac{\smile EG}{2}$$
2) $$\angle EDG$$ - вписанный $$\Rightarrow$$ $$\angle EDG=\frac{\smile EG}{2}\Rightarrow$$ $$\angle HGE=\angle EDG$$
Б) 1) $$AF=FD$$ (по условию ) $$AD=DC\Rightarrow$$ FD-средняя линия и $$FD=\frac{AB}{2}=\frac{BC}{2}$$; $$\angle HAD=\angle FDA$$
2) Пусть $$H \in BE$$; $$\angle A=\angle C=\alpha \Rightarrow$$ $$\angle FDA=\alpha$$; $$FH=2x\Rightarrow$$ $$HE=3x$$
3) из $$\Delta AFD$$: $$\angle AFD=180-2\angle A=180-2\alpha$$; Из AEOD: $$\angle O=180-\angle A=180-\alpha$$; $$\angle DGE=\frac{\smile ED}{2}=\frac{\angle O}{2}=90-\frac{\alpha }{2}$$
Из $$\Delta EFG$$: $$\angle FEG +\angle EFG=\angle DGE\Rightarrow$$ $$\angle FEG=\angle DGE-\angle EFG=\frac{3\alpha }{2}-90$$
4) $$\Delta EGH$$ – равнобедренный (образован касательными) $$\Rightarrow$$ $$\angle HGE=HEG=\frac{3\alpha }{2}-90\Rightarrow$$ $$\angle GHF=2\angle HGE=3\alpha -180$$(внешний угол $$\Delta EGH$$)
5) $$\Delta FGH=180-\angle GHF-\angle F=180-\alpha$$ (из $$\Delta EGH$$)
6) из $$\Delta FHG$$: по т. Синусов: $$\frac{FH}{\sin \angle FGH}=\frac{HG}{\sin \angle GHF}$$, но $$HG=HE\Rightarrow$$ $$\frac{2x}{\sin (180-\alpha )}=\frac{3x}{\sin (180-2\alpha )}\Leftrightarrow$$ $$\frac{2}{\sin \alpha }=\frac{3}{\sin 2\alpha }\Leftrightarrow$$ $$2 \sin 2\alpha -3 \sin \alpha =0\Leftrightarrow$$ $$4 \sin \alpha \cos \alpha -3 \sin \alpha =0 \Leftrightarrow$$ $$\sin \alpha (4 \cos \alpha -3)=0 \Leftrightarrow$$ $$\cos \alpha =\frac{3}{4}\Rightarrow$$ $$\alpha =arccos \frac{3}{4}$$($$\sin \alpha$$ не может быть 0 )
Задание 16
Два одинаковых поля требуется вспахать тремя тракторами. При работе в одиночку первый трактор вспашет одно поле втрое быстрее, чем второй, а третьему на ту же работу потребуется времени на два часа больше, чем первому. Работая вместе, все три трактора могут вспахать одно поле за семь часов двенадцать минут. Найти наименьшее время, за которое можно вспахать оба поля при условии, что все тракторы начинают работу одновременно, а для переезда с одного поля другое трактору требуется сорок минут.
Пусть объем всего поля равен 1. x - производительность 1-го трактора (часть объема в час) , y, z - второго и третьего, t - время первого в часах . Раз первый вспахает втрое быстрее , то $$y=\frac{x}{3}$$. Получим ( раз втроем вспахивают за 7 ч 12 мин.):
$$\frac{1}{x+y+z}=7\frac{12}{60}\Leftrightarrow$$ $$\frac{1}{x+\frac{x}{3}+z}=\frac{36}{5}\Leftrightarrow$$ $$5=\frac{4x}{3}*36+36z\Leftrightarrow$$ $$z=\frac{5-48x}{36}$$
Так как третий на 2 часа больше, то : $$\left\{\begin{matrix}\frac{1}{x}=t\\\frac{1}{z}=t+2\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{1}{x}=t\\\frac{36}{5-48x}=\frac{1}{x}+2\end{matrix}\right.$$
$$\frac{36}{5-48x}=\frac{1+2x}{x}\Leftrightarrow$$ $$36x=5+10x-48x-96x^{2}\Leftrightarrow$$ $$96x^{2}+74x-5=0\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=\frac{1}{16}\\x_{2}<0\end{matrix}\right.$$
Пусть три трактора работают x часов на каких-то полях, тогда они выполняют $$\frac{5}{36}x$$ объема. Затем один или несколько переезжают (чтобы ускорить другое поле и закончить оба одновременно), тогда производительность оставшихся S и выполнят они $$S*\frac{2}{3}$$ объема . Потом все трое дорабатывают вместе y часов: $$\frac{5}{36}x+\frac{2}{3}S+\frac{5}{36}y=2\Leftrightarrow$$ $$\frac{5}{36}(x+y)=2-\frac{2}{3}S$$
Очевидно, что $$x+y\rightarrow min$$, при $$S\rightarrow max$$: $$S_{max}=\frac{1}{16}+\frac{1}{18}=\frac{17}{144}$$. Тогда : $$x+y=(2-\frac{2}{3}*\frac{17}{144})*\frac{36}{5}=$$$$\frac{415}{216}*\frac{36}{5}=\frac{83}{6}$$
Тогда общее время: $$\frac{83}{6}+\frac{2}{3}=14,5$$
Задание 17
Найдите все значения параметра a, при которых уравнение $$\left | \frac{x(3^{x}-1)}{3^{x}+1} -2a\right |=a^{2}+1$$ имеет нечетное число решений.
Пусть $$(x)=\frac{x(3^{x}-1)}{3^{x}+1}$$ и $$g(x)=a^{2}+1$$
1) $$f(x) \geq 0$$ при любом x. Найдем промежутки возрастания и убывания: $${f}'(x)=\frac{(x{(3^{x}-1)}'(3^{x}+1)-{(3^{x}+1)}'(x(3^{x}-1)))}{(3^{x}+1)^{2}}=0|* (3^{x}+1)^{2}\Leftrightarrow$$$$((3^{x}-1)+x*3^{x}\ln 3)(3^{x}+1)-3 ^{x}\ln 3* x(3^{x}-1)=0\Leftrightarrow$$ $$3 ^{2x}-1+3^{2x}*x\ln 3+x*3^{x}\ln 3-x*3^{2x}\ln 3 +3 ^{x}*x\ln 3=0\Leftrightarrow$$ $$3 ^{2x}-1+2x*3^{2x}\ln 3=0\Leftrightarrow$$ $$3^{2x}+2x*3 ^{x}\ln 3=1\Leftrightarrow$$ $$1-2x\ln3=3^{x}$$
Пусть $$m(x)=1-2x\ln 3$$ и $$n(x) =3^{x}$$: m(x) - линейная убывающая и n (x)-степенная возрастающая $$\Rightarrow$$ одна точка пересечения x=0
Для f(x): x=0 - точка минимума $$\Rightarrow$$ $$(-\infty ; 0)$$ – убывает монотонно, $$(0; +\infty )$$ - возрастает . При этом
$$\left | \frac{x(3^{x}-1)}{3^{x}+1}-2a \right |=f_{1}(x)$$ - это график f(x), у которого вся часть графика под Ox отражается симметрично относительно Ox. g(x) –прямая, параллельная Ox ($$a^{2}+1>0$$, при любом a ). Тогда возможен только один вариант нечетного числа корней, когда $$\left | 2a \right |=a^{1}+1\Leftrightarrow$$ $$a^{2}-\left | 2a \right |+1=0\Leftrightarrow$$ $$(\left | a \right |-1)^{2}=0\Leftrightarrow$$ $$a=\pm 1$$
2) Возможно решение с использованием инвариантности: доказать четность левой функции (f(-x)=f(x)), тогда нечетное количество решений будет лишь в том случае, когда один из корней равен 1. Подставить вместо х в начальное уравнение 1 и получим сразу уравнение отностильно а
Задание 18
В последовательности 19752... каждая цифра, начиная с пятой, равна последней цифре суммы предыдущих четырёх цифр. Встретится ли в этой последовательности:
А) Рассмотрим последовательность: 19752.. Сначала идет сумма 4 нечетных , что даст четное. Затем получим 19752d , где d –нечетное (т.к. получается из суммы трех нечетных (9,7,5) и четного) Далее , аналогично , из 19752defgh, цифры e,f,g-нечетные и h-четные . Т.е. будет всегда на 4 нечетных и 1 четное , тогда 1234 и 3269 не получается никак.
Б) Докажем, что четверка цифр однозначно и единственно определяет последующее и предыдущее . Пусть дано a b c d. Допустим, что не определяет, тогда есть числа m и n такие, что $$\frac{m+a+b+c}{10}$$ и $$\frac{n+a+b+c}{10}$$ в остатке даст d. Тогда $$m-n$$ кратно 10 , но m и n цифры от 0 до 9 и не могут в разности быть кратны 10. Значит доказано. Но последовательность вида a b c d не могут быть больше 10^{4} (каждая цифра от 0 до 9 - 10 штук и всего их 4), то есть они могут повториться в силу единственности определения последующего $$\Rightarrow$$ 1975 снова появится.
В) Раз 1975 снова появятся , то перед ним однозначно будет 8, т.к. $$\frac{8+1+9+7}{10}$$ в остатке дает 5.