268 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 268 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №268 (alexlarin.com)
Решаем ЕГЭ 268 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №268 (alexlarin.com)
Задание 1
Показания счётчика электроэнергии 1 февраля составляли 71 181 кВт ∙ ч, а 1 марта ‐ 71 326 кВт ∙ ч. Сколько нужно заплатить за электроэнергию за февраль, если 1 кВт ∙ ч электроэнергии стоит 5 рублей 20 копеек? Ответ дайте в рублях.
Наработка электроэнергии за февраль составила : 71326-71181=145 кВт*ч Заплатить необходимо : 145*5,2=754 рублей
Задание 2
На рисунке точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности точки на рисунке соединены линией. Определите по рисунку, сколько дней во второй половине данного периода выпало менее 1 мм осадков.
Вторая половина с 15 числа . Менее 1 или осадков было 17,19-24, что составляет 7 дней.
Задание 3
Найдем ее как сумму площадей двух треугольников: $$S=\frac{1}{2}*7*3+\frac{1}{2}*7*4=$$$$\frac{1}{2}*7*7=24,5$$
Задание 4
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 спортсменов из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким‐либо бадминтонистом из России.
Кроме Руслана есть еще 9 спортсменов из России. Всего же участников кроме него 25 человек .Тогда вероятность игры с участниками из России составит $$P=\frac{9}{25}=0,36$$
Задание 5
Найдите корень уравнения $$\frac{1}{\log_{4} (2x+1)}=-2$$
$$\frac{1}{\log_{4}(2x+1)}=-2\Leftrightarrow$$ $$\left\{\begin{matrix}\log_{4}(2x+1)=-\frac{1}{2}\\2x+1>0\\2x+1\neq 1\end{matrix}\right.$$$$\Leftrightarrow$$ $$2x+1=4-\frac{1}{2}\Leftrightarrow$$ $$2x+1=\frac{1}{2}\Leftrightarrow$$ $$2x=-\frac{1}{2}\Leftrightarrow$$ $$x=-0,25$$
Задание 6
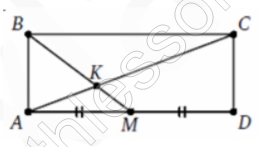
Стороны прямоугольника AB=9 и BC =24. Точка M —середина стороны DA. Отрезки AC и MB пересекаются в точке K. Найдите BK.
1) Из $$\Delta ABM$$: $$BM=\sqrt{AB^{2}+AM^{2}}=15$$
2) $$\angle KBC=\angle BMA$$ (накрест лежащие ); $$\angle BKC=\angle AKM$$ (вертикальные )$$\Rightarrow$$ $$\Delta BKC\sim \Delta AKM$$$$\Rightarrow$$ $$\frac{BK}{AM}=\frac{BK}{KM}=\frac{BC}{AM}=\frac{2}{1}$$$$\Rightarrow$$ $$BK=\frac{2}{3}BM=10$$
Задание 7
На рисунке изображен график y=F(x) одной из первообразных некоторой функции f(x) , определенной на интервале (−6; 8). Определите количество целых чисел xi, для которых f(xi) положительно.
Если y=F(x)-первообразная для y=f(x), то y=f(x)-производная для y=F(x). Тогда f(x)>0 если F(x) –возрастает $$\Rightarrow$$ $$x\in (-3 ;0)\cup (3,5; 6)$$ .На этих промежутках 4 целых значений (-2; -1; 4; 5)
Задание 8
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 9. Найдите объём пирамиды.
1) $$BC\perp DC\Rightarrow$$ по теореме о трех перпендикулярах $$SC\perp DC\Rightarrow$$ $$\angle SCB=60$$; аналогично : $$\angle SBC=60\Rightarrow$$ $$\Delta SCB$$ - равносторонний
2) Пусть $$SH\perp BC\Rightarrow$$ $$SH=9\Rightarrow$$ из $$\Delta SCH$$: $$SC=\frac{SH}{\sin SCH}=\frac{9}{\frac{\sqrt{3}}{2}}=$$$$\frac{18}{\sqrt{3}}\Rightarrow$$ $$SC=BC=\frac{18}{\sqrt{3}}$$
3) из $$\Delta SHM$$: $$MH=\frac{SH}{tg SMH}=$$$$\frac{9}{\sqrt{3}}=AB$$
4) $$V_{ABCD}=\frac{1}{3} S_{ABCD}SH=$$$$\frac{1}{3}*\frac{18}{\sqrt{3}}*\frac{9}{\sqrt{3}}*9=162$$
Задание 9
Найдите значение выражения $$\log_{9} (\log_{3}\sqrt[3]{3})$$
$$\log_{9}\log_{3}\sqrt[3]{3}=$$$$\log_{9}(\frac{1}{3} log_{3}3)=$$$$\log_{3^{2}}3^{-1}=-\frac{1}{2}=-0,5$$
Задание 10
При вращении бидона с водой на верёвке в вертикальной плоскости вода не выливается из него, если сила её давления на дно бидона неотрицательна во всех точках траектории. В верхней точке траектории сила давления воды на дно минимальна и равна $$P=m(\frac{v^{2}}{L}-g)$$ (Н), где m – масса воды в кг, v – скорость движения бидона в м/с, L – длина веревки в метрах, g = 10 м/с2 – ускорение свободного падения. С какой минимальной скоростью v надо вращать бидон, чтобы вода не выливалась из него, если длина веревки равна 48,4 см? Ответ дайте в м/с.
Давление при этом равно 0, тогда $$\frac{v^{2}}{L}-g=0$$ (т.к. $$m\neq 0$$). Получим ( с учетом , что 48,4 см =0,484 м ): $$\frac{v^{2}}{0,484}-10=0\Rightarrow$$ $$v^{2}=4,84\Rightarrow$$ $$v=\pm 2,2$$ м\с. Отрицательной быть не может $$\Rightarrow$$ 2,2
Задание 11
Для консервирования 10 кг баклажан необходимо 0,5 л столового уксуса (10%‐й раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80%‐й раствор уксусной кислоты). Сколько миллилитров уксусной эссенции понадобится хозяйке для консервирования 20 кг баклажан?
Для консервирования 20 кг понадобится 1 л 10 % раствора. В данном растворе содержится 1*0,1=0,1 л уксусной кислоты . При этом в эссенции ее 80% тогда:
$$x=\frac{0,1*100}{80}=0,125$$ л необходимо 80% раствора или 125 мл
Задание 12
Найдите наименьшее значение функции $$y=-\frac{4x^{2}+4x+7}{4x^{2}+4x+3}$$
Преобразуем данную функцию: $$y=-\frac{4x^{2}+4x+7}{4x^{2}+4x+3}=$$$$-(1+\frac{4}{4x^{2}+4x+3})=$$$$-1-\frac{4}{4x^{2}+4x+3}$$
Найдем производную: $$y^{'}=-\frac{4^{'}(4x^{2}+4x+3)-(4x^{2}+4x+3)^{'}*4}{(4x^{2}+4x+3)^{2}}=0$$$$\Rightarrow$$ $$\frac{(8x+4)*4}{4x^{2}+4x+3}=0$$$$\Rightarrow$$ $$8x+4=0\Rightarrow$$ $$x=-\frac{1}{2}$$
$$y(-2)=-\frac{4*\frac{1}{4}+4(-\frac{1}{2})+7}{4*\frac{1}{4}+4(-\frac{1}{2})+3}=$$$$-\frac{6}{2}=-3$$
Задание 13
А) Учтем, что: $$\sin \frac{x}{2}+\sin \frac{3x}{2}=$$$$2\sin \frac{\frac{x}{2}+\frac{3x}{2}}{2}\cos \frac{\frac{x}{2}-\frac{3x}{2}}{2}=$$$$2 \sin x \cos x$$
Выразим: $$2 \sin x cos \frac{x}{2}=$$$$\sin (-x)\Leftrightarrow$$ $$2 \sin x \cos \frac{x}{2}+\sin x=0\Rightarrow$$ $$\sin x(2\cos \frac{x}{2}+1)=0\Leftrightarrow$$ $$\left[\begin{matrix}\sin x=0\\2 \cos \frac{x}{2}+1=0\end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}\sin x=0\\\cos \frac{x}{2}=-\frac{1}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\pi n , n \in Z\\\frac{x}{2}=\pm \frac{2\pi}{3}+2 \pi k,k \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\pi n,n\in Z\\x=\pm \frac{4 \pi}{3}+4 \pi k, k \in Z\end{matrix}\right.$$
ОДЗ: $$\left\{\begin{matrix}\sin (-x)>0\\\sin (-x)\neq 1\\2 \sin x \cos \frac{x}{2}>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\sin x <0\\\sin x \neq -1\\\sin x \cos \frac{x}{2}>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x \in (-\pi +2 \pi n , 2 \pi n) (2)\\x \neq -\frac{\pi}{2}+2 \pi n \\\sin x \cos \frac{x}{2}>0 (1)\end{matrix}\right.$$
С учетом (2) $$x =\pi n$$ не подходит, $$x=-\frac{4 \pi}{3} +4 \pi n$$ не подходит. Подставим $$x= \frac{4 \pi}{3} + 4 \pi k$$ в (1) : $$\sin (\frac{4 \pi}{3})\cos \frac{\frac{4\pi}{3}}{2}=$$$$-\frac{\sqrt{3}}{2}\cos \frac{ \pi}{3}=$$$$-\frac{\sqrt{3}}{2}*(-\frac{1}{2})>0$$$$\Rightarrow$$ $$\frac{4 \pi}{3}+2 \pi k, k \in Z$$-корень
Б) На промежутке $$[-2 \pi ; 2 \pi]$$: $$-2 \pi\leq \frac{4 \pi}{3}+2 pi k \leq 2 \pi\Leftrightarrow$$ $$-\frac{20 \pi}{3}\leq 4 \pi\leq k\leq \frac{2 \pi}{3}\Leftrightarrow$$ $$-\frac{10}{12}\leq k\leq \frac{1}{6}\Rightarrow$$ $$k=0\Rightarrow$$ $$\frac{4 \pi}{3}+0*\pi =\frac{4 \pi}{3}$$
Задание 14
В правильной четырехугольной пирамиде SABCD с вершиной S длина перпендикуляра, опущенного из основания Н высоты пирамиды SH на грань SDC равна $$\sqrt{6}$$ , а угол наклона бокового ребра SB к плоскости основания равен 60.
A) 1) Пусть $$AB=x$$, $$\Delta ADC$$: $$AC=\sqrt{AD^{2}+DC^{2}}=x\sqrt{2}\Rightarrow$$ $$AH=\frac{x\sqrt{2}}{2}$$
2) из $$\Delta SAH$$: $$\angle ASH=90-\angle SAH=30\Rightarrow$$ $$AS=2AH=x\sqrt{2}\Rightarrow$$ $$\Delta SAC$$ - равносторонний
3) Пусть O - центр сферы $$\Rightarrow$$ OA – радиус , но это и радиус описанной около $$\Delta ASC$$.
4) из $$\Delta SAH$$: $$SH=SA*\sin SAH=x\sqrt{2}*\frac{\sqrt{3}}{2}=\frac{x\sqrt{6}}{2}$$; $$SO=\frac{2}{3}SH$$ $$\Rightarrow$$ $$SO=\frac{2}{3}*\frac{x\sqrt{6}}{2}=\frac{x\sqrt{6}}{3}$$
5) из $$\Delta SHF$$: $$HF=\frac{1}{2} AD=\frac{x}{2}\Rightarrow$$ $$SF=\sqrt{SH^{2}+HF^{2}}=$$$$\sqrt{\frac{x^{2}*6}{4}+\frac{x^{2}}{4}}=$$$$\frac{x}{2}*\sqrt{7}$$
6) $$HM*SF=SH*HF\Leftrightarrow$$ $$\sqrt{6}*\frac{x\sqrt{7}}{2}=$$$$\frac{x\sqrt{6}}{2}*\frac{x}{2}\Rightarrow$$ $$\frac{x}{2}=\sqrt{7}\Rightarrow$$ $$x=2\sqrt{7}$$
7) $$SO=\frac{2\sqrt{7}*\sqrt{6}}{3}=\frac{2\sqrt{42}}{3}$$
Б) 1) Пусть $$A _{1}B_{1}C_{1}D_{1}$$ – сечение пирамиды, т.к. проведено через середину высоты и параллельно основанию, то $$\frac{S_{A_{1}B_{1}C_{1}D_{1}}}{S_{ABCD}}=\frac{1}{4}$$; $$S_{ABCD}=x^{2}=28\Rightarrow$$ $$S_{A_{1}B_{1}C_{1}D_{1}}=7$$
2) $$SO=\frac{2}{3} SH$$; $$SL=\frac{1}{2}SH$$ , где L-середина SH , тогда $$SL=\frac{3}{4} SO$$. Пусть S-площадь диаметрального сечения сферы, $$S_{1}$$-сечение через L. Пусть ON-радиус , при этом $$LN\perp OS$$ , тогда $$OL=SO-SL =\frac{1}{4} SO\Rightarrow$$ из $$\Delta OLN$$: $$LN=\sqrt{ON^{2}-OL^{2}}=$$$$\sqrt{SO^{2}-(\frac{SO}{4})^{2}}=$$$$\frac{\sqrt{15}}{4}SO\Rightarrow$$ $$LN=\frac{\sqrt{15}}{4}*\frac{2\sqrt{42}}{3}=$$$$\frac{\sqrt{5}*\sqrt{14}}{2\sqrt{3}}$$ $$\Rightarrow$$ $$S_{1}=\frac{15*14 \pi}{4*3}=\frac{35 \pi}{2}$$
3) $$\frac{S_{1}}{S_{A_{1}B_{1}C_{1}D_{1}}}=\frac{35 \pi}{2}:7=\frac{5 \pi}{2}$$
Задание 15
Решите неравенство $$\log_{5-4x-x^{2}}(5-9x-2x^{2})\leq \log_{1-x}(1-2x)$$
ОДЗ: $$\left\{\begin{matrix}5-9x-2x^{2}>0\\1-2x>0\\5-4x-x^{2}>0\\5-4x-x^{2}\neq 1\\1-x >0\\1-x\neq 1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>-5\\x<\frac{1}{2}\\x>-5\\x<1\\x\neq -2 \pm 2\sqrt{2}\\x<1\\x\neq 0\end{matrix}\right.$$$$\Leftrightarrow$$ $$x \in (-5; -2 -2\sqrt{2})\cup (-2-2\sqrt{2}; 0)\cup (0 ;\frac{1}{2})$$
Учтем, что $$5-9x-2x^{2}=(x+5)(1-2x)$$; $$5-4x-x^{2}=(x+5)(1-x)$$. Пусть $$x+5=a$$ , $$1-2x=b$$, $$1-x=c$$
$$\log_{ac}ab\leq \log_{c}b\Leftrightarrow$$ $$\frac{\ln ab}{\ln ac}\leq \frac{\ln b}{\ln c}\Leftrightarrow$$ $$\frac{\ln a+\ln b}{\ln a+\ln c}-\frac{\ln b}{\ln c}\leq 0\Leftrightarrow$$ $$\frac{\ln a \ln c+\ln b \ln c-\ln a \ln b -\ln b \ln c}{\ln c (\ln a+\ln c)}\leq 0\Leftrightarrow$$ $$\frac{\ln a(\ln c-\ln b)}{\ln c(\ln a+\ln c)}\leq 0\Leftrightarrow$$ $$\log_{c}a \frac{\ln \frac{c}{b}}{\ln ac}\leq 0\Leftrightarrow$$ $$\log_{c}a \log_{ac}\frac{c}{b}\leq 0\Leftrightarrow$$ $$(a-1)(c-1)(\frac{c}{b}-1)(ac-1)\leq 0$$
Обратная замена: $$(x+5-1)(1-x-1)(\frac{1-x}{1-2x}-1)((x+5)(1-x)-1)\leq 0\Leftrightarrow$$ $$(x+4)(-x)(\frac{x}{1-2x})*(-x^{2}-4x+4)\leq 0\Leftrightarrow$$ $$x^{2} \frac{x+4}{1-2x}*(x-(-2+2\sqrt{2}))(x-(-2-2\sqrt{2}))\leq 0\Leftrightarrow$$$$\left[\begin{matrix}x=0\\\frac{(x+4)(x-(-2+2\sqrt{2}))(x-(-2-2\sqrt{2}))}{1-2x}\leq 0\end{matrix}\right.\Leftrightarrow$$$$x \in (-\infty; -2-2\sqrt{2}]\cup [-4 ;\frac{1}{2})\cup [-2 +2\sqrt{2} ;+\infty )$$
С учетом ОДЗ: $$(-5; -2-2\sqrt{2})\cup [-4 ;\frac{1}{2})$$
Задание 16
Отрезок KB является биссектрисой треугольника KLM. Окружность радиуса 5 проходит через вершину KB, касается стороны LM в точке B и пересекает сторону KL в точке A . Известно, что $$ML=9\sqrt{3}$$, $$KA:LB=5:6$$
A) 1) Пусть KC пересекает окружность в C.
2) По свойству хорды и секущей $$\angle ABL=\angle AKB$$; $$\angle BKC=\angle CAB$$; т.к. KB – биссектриса, то $$\angle AKB=\angle BKC \Rightarrow$$ $$\angle ABL=\angle BAC\Rightarrow$$ $$LM\left \| \right \|AC$$
3) Пусть $$AK=5x$$ $$\Rightarrow$$ $$LB=6x$$, $$AL=y$$, тогда свойству секущей и хорды : $$AL*LK=LB^{2}\Rightarrow$$ $$y(y+5x)=(6x^{2})\Rightarrow$$ $$y^{2}+5xy-36y^{2}\Rightarrow$$ $$D=(5x)^{2}+4*36x^{2}=(13x)^{2}\Rightarrow$$ $$y_{1}=4x , y_{2}<0$$
4) $$\frac{AK}{AL}=\frac{5}{4}\Rightarrow$$ $$\frac{AK}{KL}=\frac{5}{9}=\frac{AC}{LM}\Rightarrow$$ $$AC=\frac{5}{9} *9\sqrt{3}=5\sqrt{3}$$
5) из $$\Delta AKC$$: $$\frac{AC}{\sin \angle AKC}=2 R$$ , $$R =5\Rightarrow$$ $$\sin \angle AKC=\frac{5\sqrt{3}}{2*5}=$$$$\frac{\sqrt{3}}{2}\Rightarrow$$ $$\angle AKC=60$$ или 120 (120 не может, т.к. $$\frac{AK}{AL}$$ должно быть тогда < 1)
Б) 1) Пусть $$KC=5t\Rightarrow$$ $$CM=4t\Rightarrow$$ по свойству биссектрисы $$BM=6t\Rightarrow$$ $$ML=6(x+t)=9\sqrt{3}\Rightarrow$$ $$x+t=\frac{3\sqrt{3}}{2}$$
2) из $$\Delta KLM$$: $$LM^{2}=LK^{2}+KM^{2}-2 LM*KM*\cos LKM\Leftrightarrow$$ $$(6(x+t))^{2}=81x^{2}+81t^{2}-81xt\Leftrightarrow$$ $$36x^{2}+36t^{2}+72xt=81x^\Leftrightarrow$$ $$2+81t^{2}-81xt\Leftrightarrow$$ $$5x^{2}+5t^{2}-17 xt=0\Leftrightarrow$$ $$5(x+t)^{2}=27xt\Leftrightarrow$$ $$5(\frac{3\sqrt{3}}{2})^{2}=27xt\Leftrightarrow$$ $$xt=\frac{5}{4}$$
3) $$S_{LKM}=\frac{1}{2} LK*KM*\sin LKM\Rightarrow$$ $$S_{LKM}=\frac{1}{2}*9x*9t*\frac{\sqrt{3}}{2}=$$$$\frac{81xt\sqrt{3}}{4}=\frac{405\sqrt{3}}{16}$$
Задание 17
Малое предприятие выпускает изделия двух типов. Для изготовления изделия первого типа требуется 9 часов работы станка А и 11 часов работы станка Б. Для изготовления изделия второго типа требуется 13 часов работы станка А и 3 часа работы станка Б (станки могут работать в любой последовательности). По техническим причинам станок А может работать не более 130 часов в месяц, а станок Б—не более 88 часов в месяц. Каждое изделие первого типа приносит предприятию 22 000 д. е. прибыли, а каждое изделие второго типа—26 000 д. е. прибыли. Найдите наибольшую возможную ежемесячную прибыль предприятия и определите, сколько изделий первого типа и сколько изделий второго типа следует выпускать для получения этой прибыли.
Пусть выпускается xизделий 1-го типа и y изделий второго типа ($$x , y \in Z$$ и $$x, y >0$$). Составим таблицу:
Получим систему : $$\left\{\begin{matrix}9x+13y\leq 30\\11x+3y\leq 88\\1000(22x+26y)\rightarrow max\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y\leq \frac{130-9x}{13}(1)\\y\leq \frac{88-11y}{3}(2)\\2000 (11x+13y)\rightarrow max\end{matrix}\right.$$
Построим график (решение ) для (1) и (2)
Получим заштрихованную плоскость . При этом необходимо рассматривать точки ближе к прямым (1) и (2) и с целыми координатами. Так же учтем, что изделие 2 выгоднее: (1;10; (1;9); (2;8); (4;7); (5;6); (6;5);(7;3) .
Видим , что $$x+y\rightarrow max$$ при (4;7) ; (5;6) и (6;5) .Т.к. второе выгоднее то берем с большей ординатой $$\Rightarrow (4;7)$$ . То есть 4 изделия 1,7 изделие 2 и прибыль : $$2000(11*4+13*7)=270000$$.
Задание 18
Найдите все значения параметра a, при каждом из которых система $$\left\{\begin{matrix}x^{3}-(a+3)x^{2}+(3a+2)x-2a\geq 0\\ x^{3}-(a+3)x^{2}+3ax\leq 0\end{matrix}\right.$$ имеет единственное решение
Рассмотрим $$f(x) =x^{3}-(a+3)x^{2}+3ax$$, тогда в первом неравенстве записано $$f(x) +2x-2a\geq 0\Rightarrow$$ $$f(x)\geq 2a-2x$$. Пусть $$2a-2x=g(x)$$ , тогда имеем $$\left\{\begin{matrix}f(x)\geq g(x)\\g(x)\leq 0\end{matrix}\right.$$ и оно должно иметь единственное решение . При этом g(x) – прямая, функция убывает. Рассмотрим $$f(x)$$:
$$x^{3}-(a+3)x^{2}+3ax=$$$$x(x^{2}-(a+3)x+3a)=$$$$x(x^{2}-ax-3x+3a)=$$$$x(x(x-a)-3(x-a))=x(x-a)(x-3)$$
Изобразим схематичное решение системы:
Очевидно , чтобы выполнялось условие единственного решения при $$f(x) \leq 0$$ необходимо, чтобы $$g(x_{0})=0$$. Если $$g(x_{0})>0$$ - решений нет, если $$g(x_{0})<0$$ решением будет множество точек из $$[g_{0} ;x_{0}]$$. При этом $$f(x)=0$$ при $$x=0 ;3 ;a$$.
Есть три варианта расположения а:
1) $$a<0$$: тогда $$g(3)=0\Rightarrow$$ $$2a-2*3=0\Rightarrow$$ $$a=3$$ - не подходит
2) $$0\leq a\leq 3$$ : $$g(3) =0\Rightarrow$$ $$a=3$$ - решение
3) $$a>3 \Rightarrow$$ $$g(a)=0\Rightarrow$$ $$2a-2a=0$$ – верное числовое равенство $$\Rightarrow$$ $$a>3$$
Тогда $$a \in [3; +\infty )$$
Задание 19
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три непустые группы. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
A) да могут, например 1-ая группа 2-ая группа 4;6 $$\Rightarrow$$ среднее арифметическое равно 5.
Б) Учтем, что сумма всех чисел 61. Пусть группа составляет из x,y,z элементов ($$x,y,z, \in N$$ ) , тогда $$x+y+z=10$$. Пусть среднее арифметическое для них равно k ,тогда $$kx+ky+kz=61\Rightarrow$$ $$k(x+y+z)=61\Leftrightarrow$$ $$10k=61\Rightarrow$$ $$k=6,1$$. Но тогда $$6,1x$$ - целое число(т.к. это сумма целх чисел) $$\Rightarrow$$ x кратно 10, но при этом $$x\leq 8$$, т.к. в двух остальных группах минимум 1 число $$\Rightarrow$$ не может.
B) Рассмотрим разбиение (6) ; (3;9) ; (1;2;4;5;7;8;16) .Среднее арифметическое для первых двух групп равно 6, для третьей $$\frac{43}{7}$$. Очевидно, что среднее арифметическое одной из групп больше 6 , иначе бы сумма всех чисел не превосходила бы 60. Тогда не меньше $$6k+1$$ для к чисел , и среднее арифметическое для нее не меньше , чем $$\frac{6k+1}{k}=6+\frac{1}{k}$$. Чем меньше $$\frac{1}{k}$$ , тем больше k. Минимальное количество чисел в двух других группах равно 2. Если одно из чисел больше или равно 7 , то $$\frac{43}{7}<7$$ , следовательно, не рассматриваем (т.к. нужно минимальное среднее).Иначе меньше или равно 5 , тогда среднее арифметическое для оставшихся $$\frac{(61-(5+6))}{8}=\frac{50}{8}$$ больше или равно $$\frac{50}{8}$$ , но $$\frac{50}{8}>\frac{43}{7}$$, не подходит . При $$k\leq 7$$ же среднее арифметическое больше или равно $$\frac{43}{7}\Rightarrow$$ минимум $$\frac{43}{7}$$