388 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.

$$4^x-2^x-2=0$$

$$2^2x-2^x-2=0$$

$$2^x=t, t>0$$

$$t^2-t-2=0$$

$$t=-1$$ и $$t=2$$

$$2^x=-1$$

$$\varnothing$$

$$2^x=2$$

$$x=1$$

$$P(л.б.)=P(л.б., з.1)+P(л.б., з.2)=0,025\cdot0,2+0,015\cdot0,8=0,017$$

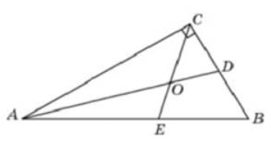
Острый угол пересечения биссектрис можно найти по формуле:

$$\angle AOE=\frac{1}{2}(\angle A+\angle C)=\frac{90^{\circ}+32^{\circ}}{2}=61^{\circ}.$$

$$g(6-x)=\sqrt[11]{(6-x)(12-(6-x))}=\sqrt[11]{(6-x)(6+x)}$$

$$g(6+x)=\sqrt[11]{(6+x)(12-(6+x))}=\sqrt[11]{(6+x)(6-x)}$$

$$\frac{g(6-x)}{g(6+x)}=\frac{\sqrt[11]{(6-x)(6+x)}}{\sqrt[11]{(6+x)(6-x)}}=1$$

$$D=\sqrt{a^2+a^2}=\sqrt{2a^2}=a\sqrt{2}=2\sqrt{2}$$

$$V=\frac{\pi D^2}{4}\cdot H=\frac{\pi\cdot4\cdot2}{4}\cdot\frac{2}{\pi}=4$$

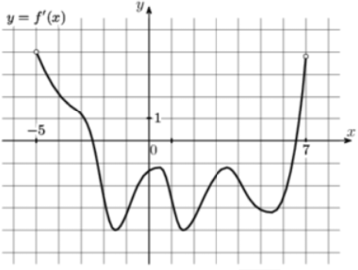
Функция убывает там, где $$f'(x)<0,$$ т.е. график производной под $$Ox$$: тогда целые от $$-2$$ до $$6$$ включительно.

$$-2-1+0+1+2+3+4+5+6=18$$

$$5\sin\pi t\geq2,5$$

$$\sin\pi t\geq0,5$$

$$​\frac{\pi}{6}+2\pi n\leq\pi t\leq\frac{5\pi}{6}+2\pi n$$​

Так как просят в течении первой секунды, то $$​n=0​$$

$$​\frac{1}{6}\leq t\leq\frac{5}{6}​$$

$$\tau=\frac{\frac{5}{6}-\frac{1}{6}}{1}=\frac{2}{3}\approx0,67$$

Пусть $$a_1=10$$ км прошел турист в первый день;

$$n = 6$$ дней,

$$a_3$$ – в третий день,

$$a_6$$ – в последний ($$n$$-ый) день.

Тогда за 6 дней турист прошел 120 км.

$$S_n=\frac{(a_1+a_n)n}{2}$$

$$120=\frac{(10+a_6)6}{2}$$

$$\frac{120}{3}=10+a_6$$

$$a_n=a_1+(n-1)d$$

$$30=10+(6-1)d$$

$$d=4$$ км - ежедневная прибавка

$$a_3=10+(3-1)4=18$$ км - в третий день

Первая прямая проходит через $$(2;-1)$$ и $$(3;1).$$

Тогда: $$\left\{\begin{matrix} -1=2k+b\\ 1=3k+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -1=4+b\\ 2=k \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=-5\\ k=2 \end{matrix}\right.$$

Получим: $$y=2x-5.$$

Вторая проходит через точки $$(0;1)$$ и $$(1;-2).$$

Тогда: $$\left\{\begin{matrix} 1=0\cdot k+b\\ -2=1\cdot k+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=1\\ k=-3 \end{matrix}\right.$$

Получим: $$y=-3x+1.$$

Тогда: $$2x-5=-3x+1\Leftrightarrow 5x=6\Leftrightarrow x=1,2$$

Если сделано 2 броска, то общее количество исходов 4 штуки (ОО; ОР; РО; РР) и только один с двумя орлами, то есть $$\frac{1}{4}$$ - вероятность 2 орлов за 2 броска.

Далее за 3 считаем: всего исходов 8, с 2 орлами 3 (ООР; ОРО; РОО), но ООР мы не считаем, так как если бы первыми двумя бросками выпали орлы, то третий не делали бы. Значит $$2\Rightarrow P=\frac{2}{8}=\frac{1}{4}.$$

За 4 броска: всего 16 исходов, 2 орла: ОРРО; РОРО; РРОО (такие как ООРР или РООР исключаем). Итого $$P=\frac{3}{8}.$$

И так далее. Получается:

При этом математическое ожидание есть сумма всех произведений количества бросков на соответствующую вероятность:

$$M(x)=\sum^{\infty}_{n=2}n\cdot\frac{n-1}{2^n}=4$$

$$y' = (2x – 3)'·\cos x + (2x – 3)·(\cos x)' – (2\sin x)´$$

$$y' = 2\cos x – (2x – 3)\sin x – 2\cos x = – (2x – 3)\sin x$$

$$y' = – (2x – 3)\sin x$$

$$y' = 0$$

$$– (2x – 3)\sin x = 0$$

$$(3 – 2x)\sin x = 0$$

$$3 – 2x = 0$$    и    $$\sin x = 0$$

Решим 1 уравнение:

$$3 – 2x = 0$$

$$x = \frac{3}{2}$$

$$x = 1,5$$

Решим 2 уравнение:

$$\sin x = 0$$

$$x = 0$$ не принадлежит промежутку $$(0;\frac{\pi}{2})$$

Отметим точку $$x = 1,5$$ на числовой прямой, учитывая промежуток $$(0;\frac{\pi}{2})$$ и найдем знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)

В точке $$x = 1,5$$ производная функции меняет знак с положительного на отрицательный, значит, это искомая точка максимума.