317 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
Задание 1
Полвека назад валовой внутренний продукт (ВВП) страны А был на 20 % больше, чем у страны В. С тех пор страна А увеличила ВВП на 55 %, а страна В ? увеличила на 50 %. Найдите на сколько процентов ВВП страны А стал больше, чем у страны В.
Пусть x - ВВП A, y - ВВП B. Тогда $$x=1,2*y$$.
Далее $$x \to 1,55*y, y \to 1,5*y$$.
Получим: $$1,5*y-100%;1,55*x-a%$$
При этом: $$1,55*x=1,55*1,2*y=1,86*y$$
Тогда $$a= \frac{1,86*y*100\%}{1,5*y}=124\% \to$$ на $$24\%$$
Задание 2
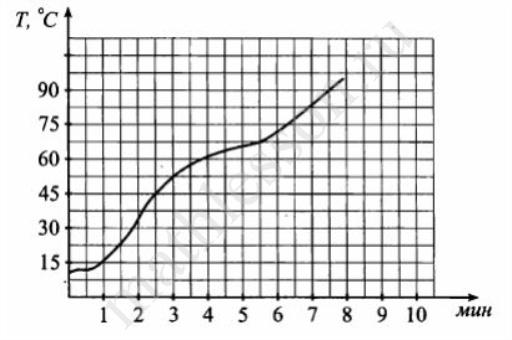
На графике показан процесс нагревания чайника. На оси абсцисс откладывается время в минутах, прошедшее с момента включения чайника, на оси ординат - температура чайника в градусах Цельсия. Определите по рисунку, за сколько минут чайник нагреется от $$45^\circ $$ до $$90^\circ $$
Задание 3
Найдите градусную меру угла АОВ, изображенного на рисунке:
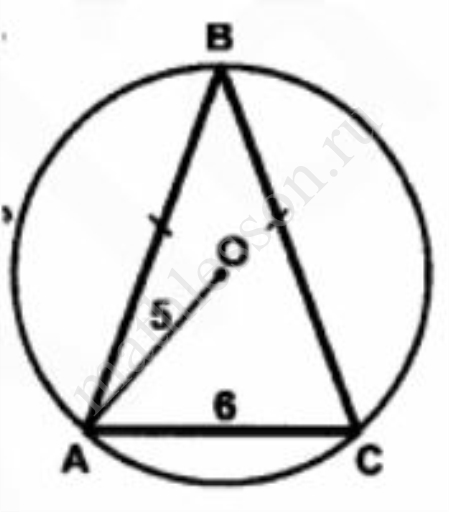
$$\angle ACB$$ - вписанный $$\to \cup AB=2\angle ACB=200^\circ \to$$ $$\cup ACB=360^\circ -200=160^\circ \to т.к. \angle AOB$$ - центральный,то $$\angle AOB= \cup ACB=160^\circ $$
Задание 4
Событие A «выиграет хотя бы одну встречу» противоположно событию B «проиграет все встречи». При этом вероятность последующего проигрыша увеличивается. Тогда $$P\left(B\right)=0,5*0,6*0,7=0,21\to P\left(A\right)=1-P\left(B\right)=0,79$$
Задание 5
$$\left(x^2-x-12\right)*{{\log }_{0,2} \left(2-x\right)=0\ }\ \to \left\{ \begin{array}{c} \left[ \begin{array}{c} x^2-x-12=0 \\ 2-x=1 \end{array} \right. \\ 2-x>0 \end{array} \right.\leftrightarrow$$ $$\left\{ \begin{array}{c} \left[ \begin{array}{c} x=4 \\ x=-3 \\ x=1 \end{array} \right. \\ x<2 \end{array} \right.\to x=\left(-3\right)+1=-2$$
Задание 6
Найдите площадь треугольника АВС, изображенного на рисунке.
Задание 7
Найдите координату $$x$$ точки, в которой касательная к графику функции $$y=\frac{x^2}{2}$$ точке $$x_0=4$$ пересекает ось абсцисс.
Задание 8
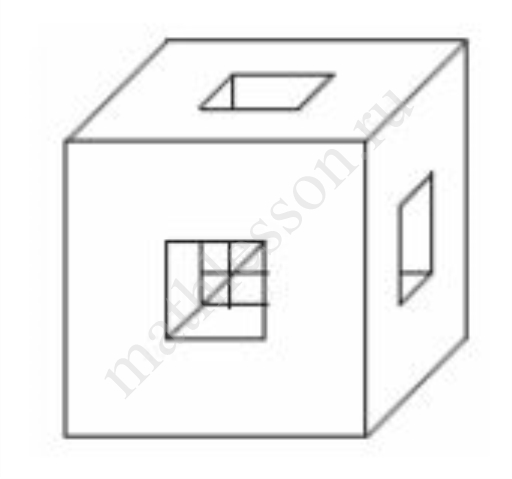
Для каждой грани куба с ребром 6 проделали сквозное квадратное отверстие со стороной квадрата 2. Найдите объем оставшейся части.
Задание 9
Найдите значение выражения $${{\log }_{{\tan \frac{\pi }{3}\ }} {27}^{{\cos \frac{\pi }{3}\ }}\ }+{{\log }_{{\cot \frac{\pi }{3}\ }} 9^{{\sin \frac{\pi }{6}\ }}\ }$$.
Задание 10
На рельсах стоит платформа. Скейтбордист прыгает на нее со скоростью $$v=6$$ м/с под острым углом $$\alpha $$ к рельсам. От толчка платформа начинает ехать со скоростью $$u=\frac{m}{m+M}*v*{\cos \alpha \ }$$, где $$m=75\ $$кг -- масса скейтбордиста со скейтом, а $$M=375$$ кг -- масса платформы. Под каким наибольшим углом $$\alpha $$ (в градусах) нужно прыгать, чтобы разогнать платформу до скорости не менее чем 0,5 м/с.
Подставим значения в формулу: $$0,5=\frac{75}{75+375}*6*\cos \alpha \to \cos \alpha=\frac{0,5*450}{6*7,5}=0,5; \alpha \in \left[0;90\right]\to \alpha =60^{\circ}$$
Задание 11
Имеются два раствора с разным процентным содержанием соли. Если смешать 1 кг первого раствора и 3 кг второго, то полученный раствор будет содержать 32,\% соли. Если смешать 3,5 кг первого раствора и 4 кг второго, то полученный раствор будет содержать 26% соли. Каким будет процентное содержание соли в растворе, если смешать равные массы первого и второго растворов?
Пусть $$x$$ - доля соли в первом растворе $$\to x\ и\ 3,5*x\ кг$$ -- масса соли в первом растворе в двух случаях. $$y$$ - доля во втором растворе $$\to 3*y\ и\ 4*y\ кг$$ - масса.
Возьмем по 1 кг, тогда соли 0,1 кг и 0,4 кг, концентрация $$\frac{0,1+0,4}{2}=0,25\to 25\%$$
Задание 12
Найдите наименьшее значение функции $$y=\sqrt[5]{-\frac{5*x^4}{4}+4*x^5}$$ на интервале $$\left(0;;\frac{1}{2}\right)$$
Найдем производную: $$y^{'}={\left({\left(-\frac{5*x^4}{4}+4*x^5\right)}^{\frac{1}{5}}\right)}^{'}=$$$$\frac{1}{5}*{\left(-\frac{5*x^4}{4}+4*x^5\right)}^{\frac{4}{5}}*{\left(-\frac{5*x^4}{4}+4*x^5\right)}^{'}=$$$$\frac{1}{5}*\frac{1}{\sqrt[5]{{\left(-\frac{5*x^4}{4}+4*x^5\right)}^4}}*\left(-5*x^3+20*x^4\right)=0$$ $$-5*x^{3}*\left(1-4*x\right)=0\to x=0$$ и$$x=\frac{1}{4};$$ $$\left(\frac{1}{4}\right)=\sqrt[5]{\frac{-5*{(\frac{1}{4})}^4}{4}+4*{\left(\frac{1}{4}\right)}^5}=$$$$\sqrt[5]{-{\left(\frac{1}{4}\right)}^5}=-0,25$$
Задание 13
а) Решите уравнение $$\frac{{\cos 2x*{\cos 8x\ }-{\cos 10x\ }\ }}{{\cos x\ }+1}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$\left[0;;\pi \right]$$
Задание 14
В правильной треугольной призме $$ABCA_1B_1C_1$$ через середину $$D$$ ребра $$CC_1$$ проведено сечение $$ADB_1$$.
а) Найдите, в каком отношении сечение делит объем призмы.
б) Найдите угол между плоскостями $$ABC$$ и $$ADB_1$$, если боковые ребра равны 2, а стороны основания равны 5.
Задание 17
В декабре 2020 года планируется взять кредит в банке в размере $$S$$ млн рублей сроком на 36 месяцев. Условия его возврата таковы:
-- 1-го числа каждого месяца, начиная с января 2021 года, долг возрастает на $$0,8\%$$ по сравнению с концом предыдущего месяца;
-- со 2-го по 14 число каждого месяца, начиная с января 2021 года, необходимо выплатить часть долга;
-- 15-го числа каждого месяца, начиная с января 2021 года, долг должен уменьшиться на одну и ту же величину.
Известно, что в период с 02.12.2021 по 14.08.2022 включительно, нужно выплатить банку 1,752 млн рублей. Найдите S. Какая сумма будет выплачена банку в период по 14.12.2021 включительно?
Задание 19
Натуральное число $$A$$ таково, что, если его первую цифру переставить на последнее место, получится число, в $$n>1$$ раз меньше числа $$A$$.
а) Существует ли двухзначное число $$A$$, удовлетворяющее указанным условиям?
б) Найдите наименьшее число $$A$$, удовлетворяющее указанным условиям, если $$n=5$$, а число $$A$$ начинается с цифры 7. в) Приведите пример числа, которое при перестановке его первой цифры на последнее место увеличивается в 3 раза.