260 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 260 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №260 (alexlarin.com)
Решаем ЕГЭ 260 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №260 (alexlarin.com)
Задание 1
Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?
Пусть 3500 руб -100% , а 2800 руб - x% , тогда $$x=\frac{2800}{3500}*100=80$$% $$\Rightarrow$$ снижение на 20%
Задание 2
На графике показано изменение кинетической энергии Е движущегося тела (в килоджоулях) в зависимости от времени t (в минутах). На сколько килоджоулей увеличится кинетическая энергия тела в течение второго часа движения?
Найдем значение энергии в начале и конце второго часа: E(60)=9; E(120)=15 $$\Rightarrow$$ увеличение в течение второго часа на 15-9=6 кДж
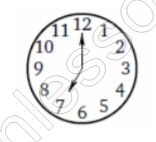
Задание 3
Между 7:00 и 12:00 располагается 5 часов. Весь круг -12 часов или 360 градусов , тогда 1 час - $$\frac{360}{12}=30$$ градусов , а 5 часов - 30*5=150 градусов
Задание 4
Витя пишет на доске любую цифру от 1 до 8. После этого Наташа рядом (либо справа, либо слева) приписывает также любую цифру от 1 до 8. Найдите вероятность того, что записанное двузначное число будет делиться на 7. Ответ округлите до сотых.
Всего чисел возможных от 11 до 88 - N=78 штук (88-10). При этом делятся на 7 из них $$n=div(\frac{88}{7})-div(\frac{11}{7})=11$$ (разность целых частей от деления). Но следует учитывать, что цифра 0 и 9 в записи не участвовала. Следовательно, из N необходимо исключить числа 19,20,29,30,39,40,49,50,59,60,69,70,79,80. Тогда чисел остается 64. А из n числа 49 и 70, то есть останется их 9. Рассматривать ситуации, когда справа или слева ставится цифра нет смысла, так количество возможных исходов (64) удвоится, но и количество делящихся на 7 (9) тоже удвоится. Тогда $$P=\frac{9}{64}\approx 0,14$$
Задание 5
из $$\Delta OBP$$: $$OP=\sqrt{OB^{2}+BP^{2}}=25$$ Пусть h-высота $$\DeltaOBP$$ из B. Тогда: $$h=\frac{OB*BP}{OP}=6,72\Rightarrow$$ $$AB=2h=13,44$$
Задание 6
F(x) - первообразная функции f(x)=3x2+2x, причем ее график проходит через точку (2;‐3). Найдите F(-2)
$$F(x)=\int f(x) dx=x^{3}+x^{2}+c$$. Т.к. F(x) проходит через (2;-3), то F(2)=-3 $$-3=2^{3}+2^{2}+c\Leftrightarrow$$ $$c=-15$$. Тогда :$$F(-2)=(-2)^{3}+(-2)^{2}-15=-19$$
Задание 7
В конус вписан цилиндр так, что плоскость его верхнего основания делит высоту конуса пополам. Найдите объем цилиндра, если объем конуса равен 12.
Пусть R-радиус основания большого конуса, h-его высота, тогда $$V=\frac{1}{3}\pi R^{2} h=12$$ – его объем . Пусть r-радиус основания цилиндра ,тогда: $$r=\frac{R}{2}$$ и m-его высота, тогда $$m=\frac{h}{2}$$ Объем цилиндра: $$V_{1}= \pi r^{2}m=\pi *\frac{R^{2}}{4}*\frac{h}{2}=$$$$\frac{\pi R^{2}h}{8}=\frac{36}{8}=4,5$$
Задание 8
Найдите значение выражения $$\frac{\sin 26^{\circ}-\sin 86^{\circ}}{2\sin 34^{\circ}}$$
$$\frac{\sin 26-\sin 86}{2 \sin 34}=$$$$\frac{2 \sin \frac{26-86}{2} \cos \frac{26+86}{2}}{2 \sin 34}=$$$$\frac{\sin (-30) \cos 56}{\sin (90-56)}=$$$$\frac{-\frac{1}{2} \cos 56}{\cos 56}=-0,5$$
Задание 9
Автомобиль, масса которого равна m=2400 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S=480 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно $$F=\frac{2mS}{t^{2}}$$ . Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 4 кН. Ответ выразите в секундах.
$$F=\frac{2m S}{t^{2}}\Rightarrow$$ $$t^{2}=\frac{2mS}{F}\Rightarrow$$ $$t=\sqrt{\frac{2mS}{F}}$$ $$t=\sqrt{\frac{2*2400*480}{4000}}=24$$
Задание 10
Из пункта F круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 15 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Пусть x км\ч– скорость велосипедиста , y км\ч – скорость мотоциклиста. Раз выехал через 30 минут (0,5 часа) и догнал через 15 минут (0,25 часа) , то: $$(0,5+0,25)x=0,25y\Leftrightarrow$$$$y=3x$$. Раз второй раз догнал (опередил на 30 км.) через 30 минут (0,5 часа) , то: $$0,5y-0,5x=30\Leftrightarrow$$$$y-x=60$$. Тогда : $$3x-x=60\Rightarrow$$ $$x=30\Rightarrow$$ $$y=90$$
Задание 11
Найдите наименьшее значение функции $$f(x)=4^{x}-2^{x+4}+100$$
$$f(x)=4^{x}-2^{x+4}+100=2^{2x}-16*2^{x}+100$$ Пусть $$2^{x}=y>0$$, тогда $$f(y)=y^{2}-16y+100$$ - график парабола, ветви направлены вверх: Найдем вершину параболы (в ней будет $$f_{min}(y)$$ при y>0): $$y_{0}=-\frac{-16}{2}=8\Rightarrow$$ $$f(18)=8^{2}-16*8+100=36$$
Задание 12
A) $$\frac{\sin 3x}{1+2 \cos 2x}=0\Leftrightarrow$$ $$\left\{\begin{matrix}\sin 3x=0\\\cos 2x\neq -\frac{1}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}3x=\pi n , n \in Z\\2x\neq \pm \frac{2 \pi}{3}+2 \pi n , n \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi n }{3} , n \in Z\\x\neq \pm \frac{\pi}{3} +\pi n , n \in Z\end{matrix}\right.$$
Рассмотрим полученные корни и ограничения (черными - корни, пустые - ограничения):
С учетом полученных пересечений получим итоговое решение : $$x=\pi n , n \in Z$$
Б) На промежутке $$[-\pi; \pi)$$ получим следующие корни: $$-\pi$$ и $$0$$
Задание 13
В пирамиде SBCD каждое ребро равно 3. На ребре SB взята точка А так, что SA:AB=1:2.
A) 1) Пусть SO - высота SBCD. Опустим $$AM\perp (BCD)$$, тогда $$\DeltaAMB\sim \Delta SOB$$: $$\frac{AM}{SO}=\frac{AB}{SB}=\frac{2}{3}$$
2) $$V_{SBCD}=\frac{1}{3} SO*S_{BCD}$$; $$V_{ABCD}=\frac{1}{3} AM*S_{BCD}\Rightarrow$$$$V_{ABCD}=\frac{AM}{SO}*V_{SBCD}=\frac{2}{3}V_{SBCD}\Rightarrow$$, пусть V - оставшаяся часть: $$V=\frac{1}{3}V_{SBCD}\Rightarrow$$ $$\frac{V_{ABCD}}{V}=\frac{2}{1}$$
Б) 1) $$CA=AD\Rightarrow$$ $$\Delta ACD$$ - равнобедренный. Из $$\Delta SAC$$: $$CA=\sqrt{CS^{2}+SA^{2}-2 CS*SA *\cos S}=\sqrt{7}$$
2) Рассмотрим пирамиду SADC, введем ортогальную систему координат , как показано на рисунке, где N - центр, описанной окружности около $$\Delta SCD$$
3) Центр сферы будет лежать на оси Oz. Пусть Q - центр сферы, тогда $$Q (0;0;z)$$ и QS=QA (как радиусы сферы). Зададим координаты QS и QA; $$A(NA_{x}; O; AA_{x})$$, где $$A_{x}$$ - проекция A на (SDC) ; $$S(NS;0;0)$$
4) из $$\Delta CSD$$: $$SH=SD* \sin D=3*\frac{\sqrt{3}}{2}$$; $$SN=\frac{2}{3} SH=\sqrt{3}\Rightarrow$$ $$S(\sqrt{3}; 0;0)$$
Из $$\Delta ADC$$: $$AH=\sqrt{AD^{2}-HD^{2}}=\frac{\sqrt{19}}{2}$$; Из $$\Delta ASH$$: $$\cos S=\frac{AS^{2}+SH^{2}-AH^{2}}{2 AS*SH}=\frac{1}{\sqrt{3}}\Rightarrow$$ $$\sin S=\frac{\sqrt{2}}{\sqrt{3}}\Rightarrow$$ $$SA_{x}=AS*\cos S=\frac{1}{\sqrt{3}}\Rightarrow$$ $$NA_{x}=NS-SA_{x}=\frac{2\sqrt{3}}{3}$$; $$AA_{x}=SA*\sin S=\frac{\sqrt{2}}{\sqrt{3}}$$. Тогда A $$(\frac{2\sqrt{3}}{3};0; \frac{\sqrt{2}}{\sqrt{3}})$$, следовательно:
$$QS(\sqrt{3}-0;0-0; 0-z)=(\sqrt{3};0;-z)$$ и $$QA(\frac{2\sqrt{3}}{3}-0;0-0;\frac{\sqrt{2}}{\sqrt{3}}+z)=(\frac{2\sqrt{3}}{3};0; \frac{\sqrt{2}}{\sqrt{3}}+z)$$
Тогда длины: $$\left | QS \right |=\sqrt{(\sqrt{3})^{2}+(-z)^{2}}$$ и $$\left | QA \right |=\sqrt{(\frac{2\sqrt{3}}{3})^{2}+(\frac{\sqrt{2}}{\sqrt{3}}+z)^{2}}$$. В итоге получим:
$$QS^{2}=QA^{2}\Leftrightarrow$$ $$3+z^{2}=\frac{4}{3}+\frac{2}{3}+\frac{2\sqrt{2}}{\sqrt{3}}z+z^{2}\Leftrightarrow$$ $$\frac{2\sqrt{2}}{\sqrt{3}}z=1\Leftrightarrow$$ $$z=\frac{\sqrt{3}}{2\sqrt{2}}$$
Тогда $$QS=\sqrt{(\sqrt{3})^{2}+(\frac{\sqrt{3}}{2\sqrt{2}})^{2}}=$$$$\sqrt{\frac{27}{8}}=\frac{3}{2}\sqrt{\frac{3}{2}}$$
Задание 14
Решите неравенство: $$(\log_{x+2} 4)(\log_{4}(x^{2}+x-2))\leq 1$$
ОДЗ: $$\left\{\begin{matrix}x+2>0\\x+2\neq 1\\x^{2}+x-2>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x+2>0\\x+2\neq 1\\(x+2)(x-1)>0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x>-2\\x\neq -1\\x>1\end{matrix}\right.\Leftrightarrow$$ $$x>1$$
Решение: $$(\log_{x+2}4)(\log_{4}(x+2)(x-1))\leq 1\Leftrightarrow$$ $$(\log_{x+2}4)(\log_{4}(x+2)+\log_{4}(x-1))\leq 1\Leftrightarrow$$ $$\frac{\log_{4}(x+2)}{\log_{4}(x+2)}+\frac{\log_{4}(x-1)}{\log_{4}(x+2)}\leq 1\Leftrightarrow$$ $$1+\log_{(x+2)}(x-1)\leq 1\Leftrightarrow$$ $$\log_{(x+2)}(x-1)\leq 0\Leftrightarrow$$ $$(x-1-1)(x+2-1)\leq 0\Leftrightarrow$$ $$(x-2)(x+1)\leq 0\Leftrightarrow$$$$\left\{\begin{matrix}x\geq -1\\x\leq 2\end{matrix}\right.$$
С учетом ОДЗ: x $$\in (1; 2]$$
Задание 15
В треугольнике АВС угол В равен 600. Через точки А и В проведена окружность радиуса 3, касающаяся прямой АС в точке А. Через точки В и С проведена окружность радиуса 4, касающаяся прямой АС в точке С.
A) 1) Пусть $$O_{1}A=R_{1}=3$$; $$O_{2}C=R_{2}=4$$ - радиусы; $$\angle ACB=\alpha$$ ; $$\angle BAC=\beta$$
2) По свойству хорды и касательной: $$\smile BC=2\angle BCA=2\alpha$$ ( или $$180-2\alpha$$ ); $$\smile AB=2\angle BAC=2\beta$$ (или $$180-2\beta$$ - зависит от построения, но на решение никак не влияет).Тогда по свойству центральных углов: $$\angle BO_{1}A=2\beta$$ ; $$\angle BO_{2}C=2\alpha$$
Пусть $$O_{1}H\perp AB$$, тогда из $$\Delta O_{1}HA$$: $$HA=O_{1}A\sin \angle HO_{1}A$$, $$\angle HO_{1}A=\frac{\angle BO_{1}A}{2}\Rightarrow$$ $$HA=R_{1}\sin \beta =3\sin \beta \Rightarrow$$ $$AB=6 \sin \beta$$. Аналогично $$BC=8 \sin \alpha$$
3) По теореме синусов из $$\Delta ABC$$ : $$\frac{AB}{\sin \angle ACB}=\frac{BC}{\sin \angle BAC}\Leftrightarrow$$ $$\frac{6 \sin \beta }{\sin \alpha }=\frac{8 \sin \alpha }{\sin \beta }\Leftrightarrow$$ $$\frac{\sin \beta }{\sin \alpha }=\frac{2}{\sqrt{3}}$$
$$\frac{AC}{\sin \angle ABC}=\frac{AB}{\sin \angle ACB}\Leftrightarrow$$ $$AC= \frac{AB}{\sin ACB }* \sin ABC=\frac{6 \sin \beta }{\sin \alpha }*\frac{\sqrt{3}}{2}=6* \frac{2}{\sqrt{3}}*\frac{\sqrt{3}}{2}=6$$
Б) 1) Общая хорда пусть будет BD. Тогда OD=OB=3; $$O_{2}D=O_{2}B=4$$ - радиусы.
2) Построим $$O_{1}K\perp O_{2}C\Rightarrow$$ $$KC=O_{1}A=3\Rightarrow$$ $$O_{2}K=4-3=1$$, $$O_{1}K=AC=6\Rightarrow$$ из $$\Delta O_{1}KO_{2}$$: $$O_{2}O_{1}=\sqrt{O_{1}K^{2}+O_{2}K^{2}}=\sqrt{37}$$
3) $$DB\perp O_{1}O_{2}$$ и $$DH=HB$$. Пусть $$O_{1}H=x$$; $$O_{2}H=\sqrt{37}-x$$; $$DH=HB=y$$, тогда по т. Пифагора из $$\Delta O_{1}HD$$ и $$O_{2}HD$$: $$\left\{\begin{matrix}x^{2}+y^{2}=3^{2}\\(\sqrt{37}-x)^{2}+y^{2}=4^{2}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y^{2}=9-x^{2}\\37-2x\sqrt{37} +x^{2}+9-x^{2}=16\end{matrix}\right.$$
Тогда: $$2x\sqrt{37}=30\Leftrightarrow$$ $$x=\frac{15}{\sqrt{37}}\Rightarrow$$ $$y=\sqrt{9-\frac{225}{37}}=\frac{6\sqrt{3}}{\sqrt{37}}\Rightarrow$$ $$DB=2*\frac{6\sqrt{3}}{\sqrt{37}}=\frac{12\sqrt{3}}{\sqrt{37}}$$
Задание 16
Первая и вторая бригады, работая вместе, могут выполнить задание не более, чем за 9 дней. Вторая и третья бригады, работая вместе, могут выполнить то же задание не менее, чем за 18 дней. Первая и третья бригады, работая вместе, могут выполнить то же задание ровно за 12 дней. Известно, что третья бригада всегда работает с максимально возможной для нее производительностью труда. За сколько дней может выполнить задание одна вторая бригада?
Пусть x-производительность 1-ой бригады (частей задания в день) ; y- 2–ой и z - 3-ей бригад. Все задание примем за 1, тогда:
$$\left\{\begin{matrix}\frac{1}{x+y}\leq 9\\\frac{1}{y+z}\geq 18\\\frac{1}{x+z}=12\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x+y\geq \frac{1}{9}\\y+z\leq \frac{1}{18}\\x+z=12\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{1}{12}-x\\x+y\geq \frac{1}{9}\\y+\frac{1}{12}-x\leq \frac{1}{18}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}z=\frac{1}{12}-x\\y\geq \frac{1}{9}-x\\y\leq x-\frac{1}{36}\end{matrix}\right.$$
Получим, что $$\frac{1}{9}-x\leq y\leq x-\frac{1}{36}\Leftrightarrow$$ $$\frac{1}{9}-x\leq x-\frac{1}{36}\Leftrightarrow$$ $$2x\geq \frac{1}{9}+\frac{1}{36}=\frac{5}{36}\Rightarrow$$ $$x\geq \frac{5}{72}$$
При этом $$z \rightarrow max$$, при $$x \rightarrow min$$, тогда $$x=\frac{5}{72}\Rightarrow$$ $$z=\frac{1}{12}-\frac{5}{72}=\frac{1}{72}\Rightarrow$$ $$y+\frac{1}{72}\leq \frac{1}{18}\Rightarrow$$ $$y\frac{1}{24}\Rightarrow$$ вторая бригада может выполнить за 24 дня
Задание 17
Найдите все значения параметра a , при которых неравенство $$4a^{2}\sqrt{2-\frac{6}{\pi}\arcsin(\sqrt{3}-2x)}+\frac{12a}{\pi}\arccos(2x-\sqrt{3})-8a^{2}-3a \leq 1$$ выполняется для любых $$x \in [\frac{2\sqrt{3}-1}{4};\frac{3\sqrt{3}}{4}]$$
Пусть $$2x-\sqrt{3}=y$$, тогда с учетом, что $$x \in [\frac{2\sqrt{3}-1}{4}; \frac{3\sqrt{3}}{4}]$$ получим , что $$y \in [-\frac{1}{2}; \frac{\sqrt{3}}{2}]$$.
Следовательно, имеем: $$4a^{2}\sqrt{2+\frac{6}{\pi}\arcsin y }\leq 1+8a^{2}+3a-\frac{12a}{\pi}(\frac{\pi}{2}-\arcsin y)$$
Пусть $$\frac{6}{\pi} \arcsin y=m$$, т.к. $$y \in [-\frac{1}{2}; \frac{\sqrt{3}}{2}]$$ , то $$m \in [-1; 2]$$, тогда: $$4a^{2}\sqrt{2+m}\leq 1+8a^{2}+3a-6a+2m\Leftrightarrow$$$$4a^{2}\sqrt{2+m}\leq 2am+8a^{2}-3a+1\Leftrightarrow$$$$\sqrt{2+m}\leq \frac{m}{2a}+\frac{8a^{2}-3a+1}{4a^{2}}$$
Пусть $$f(m)=\sqrt{2+m}$$ и $$g(m)=\frac{m}{2a}+\frac{8a^{2}-3a+1}{4a^{2}}=$$$$\frac{m}{2a}+2-\frac{3a-1}{4a^{2}}$$
- g(m) – прямая, при этом $$g(m)\cap Oy$$ в точке, которая «стремится» к у=2
- f(m) – ветвь параболы . При этом необходимо , чтобы $$f(m)\geq g(m)$$ для любого $$m \in [-1;2]$$
Рассмотрим 3 случая:
1) $$a>0$$: тогда g(m) располагается в 1 и 3 четвертях . При этом, чтобы $$f(m)\geq g(m)$$ необходимо, чтобы $$f(-1)\geq g(-1)$$: $$-\frac{1}{2a}+\frac{8a^{2}-3a+1}{4a^{2}}\geq 1\Leftrightarrow$$ $$-2a=8a^{2}-3a+1\geq 4a^{2}\Leftrightarrow$$ $$4a^{2}-5a+1\geq 0\Leftrightarrow$$ $$a \in (-\infty ; \frac{1}{4}]\cup [1; +\infty)$$
С учетом , что $$a>0$$ : $$a\in (0; \frac{1}{4}]\cup [1; +\infty )$$
- При $$a\in (0; \frac{1}{4}]$$ получим , что $$\frac{8a^{2}-3a+1}{4a^{2}} >2$$ ( пересечение F(x) с Oy) , при этом $$f(0)=\sqrt{2}\Rightarrow$$ подходит.
- При $$a\in [1; +\infty )$$ получим , что $$\frac{8a^{2}-3a+1}{4a^{2}}\geq 1,5 \Rightarrow$$ тоже подходит
2) $$a<0$$. Тогда $$g(2) \geq f(2) \Leftrightarrow$$ $$\frac{2}{2a}+\frac{8a^{2}-3a+1}{4a^{2}}\geq 2\Leftrightarrow$$ $$4a+8a^{2}-3a+1\geq 8a^{2}\Leftrightarrow$$ $$a+1\geq 0\Leftrightarrow$$ $$a\geq -1$$. Т.к. $$a<0$$, то $$a \in [-1; 0)$$
3) $$a=0$$: $$0*\sqrt{2+m}\leq 0 *m+8*0-3*0+1\Leftrightarrow$$ $$0\leq 1\Rightarrow$$ подходит
В итого решение: $$a \in [-1; \frac{1}{4}]\cup [1; +\infty )$$
Задание 18
В двух группах учится одинаковое количество студентов. Каждый студент изучает по крайней мере один язык: английский или французский. Известно, что 5 человек в первой и 5 во второй группе изучают оба языка. Количество изучающих французский в первой группе в 3 раза меньше, чем во второй. Количество изучающих английский во второй группе в 4 раза меньше, чем в первой.
Пусть французский в первой группе учат x человек (и только французский, и оба языка), тогда во второй - 3x. Английский во второй y ( и только английский, и оба языка) человек, тогда в первой 4y. Всего в первой : x+4y-5 ; во второй : 3x+y-5
A) Получим: $$x+4y-5=3x+y-5\Leftrightarrow$$ $$2x=3y\Rightarrow$$ $$x=\frac{3y}{2}\Rightarrow$$ y - четное. Тогда $$x+4y-5=33\Leftrightarrow$$ $$x+4y=38\Leftrightarrow$$ $$\frac{3y}{2}+4y=38\Leftrightarrow$$ $$3y+8y=76\Leftrightarrow$$ $$y=\frac{76}{11}\in N$$ - не может
Б) Если 2 учат только английский, то всего английский учат $$2+5=7=y$$, но y - четное $$\Rightarrow$$ не может
B) $$x=\frac{3y}{2}$$. При этом $$y\geq 5$$ и y - четное . Чем меньше y, тем меньше группа $$\Rightarrow$$ $$y=6; x=9$$ (минимальное четное больше 5). Общее число в группе тогда: 9+4*6=28.