347 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Больше разборов на моем ютуб-канале
Задание 1
За один месяц нагорело $$33047-32947=100$$ кВт$$\cdot$$ч
Нужно заплатить $$100\cdot4,29=429$$ рублей
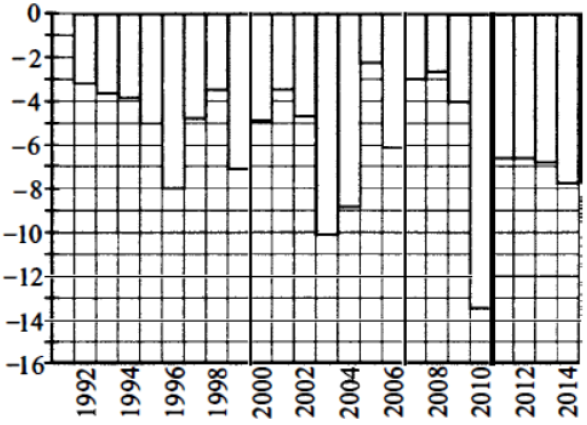
Задание 2
Столбик между 2004 и 2006 самый высокий $$\Rightarrow 2005$$
Задание 3
Найдем синус противоположного угла $$\sin\beta=\frac{3}{\sqrt{3^2+4^2}}=0,6$$
$$\sin\alpha=\sin(180-\beta)=\sin\beta=0,6$$
Задание 4
Искомой вероятностью будет сумма двух несовместных событий
$$P(A+B)=\frac{17}{51}\cdot\frac{16}{50}+\frac{34}{51}\cdot\frac{33}{50}\approx0,55$$
Событие A - это Саша попала в первую группу и Настя тоже
Событие B - Саша попала во вторую группу и Настя тоже (это независимые события)
Задание 5
$$\frac{1}{x^2-3x+2}=\frac{1}{2x^2-3x+1}\Leftrightarrow\left\{\begin{matrix} x^2-3x+2=2x^2-3x+1\\ x^2-3x+2\neq0 \end{matrix}\right.$$
Получим: $$x^2-1=0\Rightarrow x=\pm1.$$ Но при $$x=1$$ имеем $$x^2-3x+2=0,$$ значит - это посторонний корень и $$x=-1$$
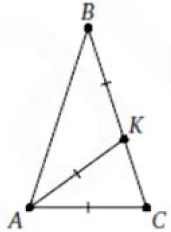
Задание 6
Пусть $$\angle A=\angle C=\alpha$$ $$\Rightarrow$$ $$\angle ABC=180-2\alpha$$
из $$\bigtriangleup AKB$$: $$\angle BAK=\angle ABK=180-2\alpha$$
из $$\bigtriangleup ACK$$: $$\angle KAC=180-2\alpha$$ $$\Rightarrow$$ $$\angle A=180-2\alpha+180-2\alpha=\alpha$$; $$360^{\circ}=5\alpha$$ $$\Rightarrow$$ $$\alpha=72$$ $$\Rightarrow$$ $$\angle ABC=180-72^{\circ}\cdot2=36$$
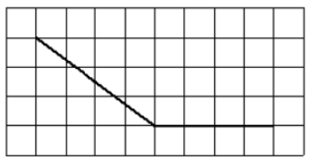
Задание 7
$$F'(x)=f(x)$$
Производная положительна там, где функция возрастает, таких точек на графике 8.
Задание 9
Возводить в степень с действительным показателем можно только положительные числа.
$$\sqrt[3]{x}\neq x^{\frac{1}{3}}$$, это разные вещи.
У нас в задаче именно $$x^{\frac{1}{3}}$$
Поэтому сразу можно написать $$4a-a^2-3>0$$ или $$a>1$$ и $$a<3$$
Разберемся с первой дробью. Хотя с ней все очевидно, мы находим корни многочлена в знаменателе, и выносим $$8^{\frac{1}{3}}=2$$ из второй скобки. Все сокращается, остается 2.
Теперь со второй дробью. Вынесем из числителя 3.
В числителе стоит $$|(3a^2-9a-12)|$$ – модуль можно раскрыть однозначно т.к. $$1<a<3$$
В итоге остается 3
$$2-(-3)=5$$
Задание 10
Задание 11
Пусть было $$x$$ кг винограда
Тогда составим уравнение для сухого вещества
$$x\cdot0,09=21\cdot0,93$$
$$x=217$$
Задание 12
В аргументе парабола – ветви вниз, наибольшее значение будет в вершине
$$x_0=-\frac{-1}{-12}=-0,5$$
$$y(-0,5)=\log_2(0,25+0,5-0,25)=-1$$
Задание 14
(Автор задачи Николай Журавлев)
Задание 17
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину $$A$$ меньше долга на 15-е число предыдущего месяца. Найдите $$n, S, A, D$$ (общая сумма выплат после погашения кредита), если известно, что четвёртая выплата составит 17 700 рублей, а девятая выплата - 16 200 рублей.