377 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$\sin\frac{\pi(5x-6)}{24}=\frac{1}{2}\Leftrightarrow\left\{\begin{matrix} \frac{\pi(5x-6)}{24}=\frac{\pi}{6}+2\pi n,n\in Z\quad|:\frac{\pi}{24}\\ \frac{\pi(5x-6)}{24}=\frac{5\pi}{6}+2\pi n,n\in Z\quad|:\frac{\pi}{24} \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} 5x-6=4+48n,n\in Z |+6|:5\\ 5x-6=20+48n \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x=2+9,6n,n\in Z\\ x=5,2+9,6n \end{matrix}\right.$$
При этом корень отрицательный и наибольший:
если $$n=0$$: $$2$$ и $$5,2$$
если $$n=-1$$: $$2-9,6=-7,6$$ и $$5,2-9,6=-4,4$$
Наибольший отрицательный $$-4,4.$$
Задание 2
Составим список возможных исходов: Всего 3 броска:
О - Орел, Р - Решка.
ООО
ОРР
ООР
ОРО
РОР
РРР
РОО
РРО
Всего 8 исходов, из них в двух случаях при первых трёх подбрасываниях выпадет одна и та же сторона монеты
$$P=\frac{2}{8}=\frac{1}{4}=0,25$$
Задание 3
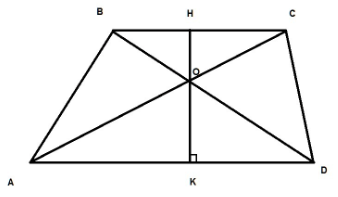
Проведем высоту HK так, чтобы она проходила через точку O.
По свойству трапеции, треугольники, образованные при пересечении диагоналей и лежащие на основаниях трапеции, подобные. Найдем коэффициент подобия:
$$k=\frac{BC}{AD}=\frac{12}{36}=\frac{1}{3}$$
Площади подобных треугольников соотносятся как квадрат коэффициента подобия:
$$\frac{S_{BOC}}{S_{AOD}}=k^2$$
$$\frac{S_{BOC}}{216}=\frac{1}{9}$$
$$S_{BOC}=24$$
Найдем высоты треугольников AOD и BOC через площадь
$$OK=\frac{2S_{AOD}}{AD}=\frac{432}{36}=12$$
$$HO=\frac{2S_{BOC}}{BC}=\frac{48}{12}=4$$
Тогда высота трапеции HK равна
$$HK=HO+OK=4+12=16$$
И площадь трапеции равна:
$$S_{ABCD}=\frac{AD+BC}{2}\cdot HK=\frac{36+12}{2}\cdot 16=384$$
Задание 4
$$x^2-10x+25=(x-5)^2\Rightarrow \sqrt[12]{(x^2-10x+25)^6}=\sqrt[12]{(x-5)^12}=|x-5|$$
Так как $$x\in (4;4,5),$$ то $$x-5<0\Rightarrow |x-5|=5-x$$
$$\sqrt{x^2-6x+9}=\sqrt{(x-3)^2}=|x-3|=x-3$$
Получим: $$5-x+x-3=2$$
Задание 5
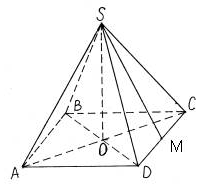
Найдем сначала площадь основания пирамиды из формулы ее объема, получим:
$$V=\frac{1}{3}S_{осн}\cdot h,$$
откуда
$$S_{осн}=\frac{3V}{h}=\frac{3\cdot784}{24}=\frac{2352}{24}=98.$$
Так как в основании правильной четырехугольной пирамиды лежит квадрат, то сторона квадрата будет равна
$$a=\sqrt{S_{осн}}=\sqrt{98}$$.
Для нахождения бокового ребра, вычислим диагональ квадрата по теореме Пифагора, получим:
$$d=\sqrt{a^2+a^2}=\sqrt{98+98}=14.$$
Известно, что высота в правильной пирамиде делит диагонали пополам. Следовательно, боковую грань можно найти из прямоугольного треугольника AOS, где AO=7, SO=24, получим:
$$AS=\sqrt{AO^2+SO^2}$$
$$AS=\sqrt{49+576}=\sqrt{625}=25$$
Задание 6
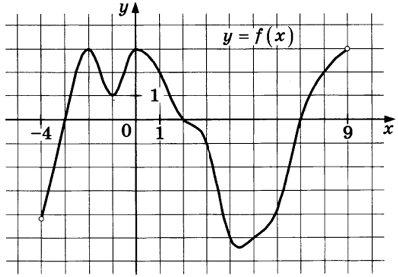
$$f'(x)>0$$ там, где $$f(x)$$ возрастает: $$(-4;-2)$$ - одно целое $$(-3);$$ $$(-1;0)$$ - 0 целых; $$(\approx4,5;9)$$ - 4 целых $$(5;6;7;8).$$ Всего 5 целых.
Задание 7
$$p_1V_1^{\alpha}=p_2V_2^{\alpha}$$
$$\frac{p_1}{p_2}=(\frac{V_2}{V_1})^{\alpha}$$
Давление уменьшилось не менее чем в 32 раза, то есть
$$\frac{p_1}{p_2}\geq32.$$ Значит, $$(\frac{V_2}{V_1})^{\alpha}\geq32$$
$$16^{\alpha}\geq32,$$ отсюда $$\alpha\geq1,25.$$
Наименьшее значение для а записываем в ответ.
Задание 8
200 г - 100%
х - 10%
$$x=200\cdot\frac{10}{100}=20$$ (г) - количество жира в мороженом
300 г - 100%
х - 6%
$$x=300\cdot\frac{6}{100}=18$$ (г) - количество жира в молоке
$$200+300=500$$ (г) - масса полученного коктейля
$$20+18=38$$ (г) - масса жира в коктейле
500 г - 100%
38 г - х%
$$x=38\cdot\frac{100}{500}=7,6\%$$ - жирность полученного коктейля
Задание 9
Вершина смещена относительно $$(0;0)$$ на 3 вправо, т.е. $$\frac{b}{k}=-3\Rightarrow b=-3k,$$ и на 2 вниз, т.е. $$c=-2.$$
Получим:
$$f(x)=|kx-3k|-2.$$
Проходит через $$(2;0).$$ Тогда:
$$0=|k\cdot2-3k|-2\Leftrightarrow |k|=2\Rightarrow k=\pm2$$
т.е. $$f(x)=|2x-6|-2=|-2x+6|-2$$
$$f(-15,7)=|2\cdot(-15,7)-6|-2=35,4$$
Задание 10
Решка выпала ровно 3 раза: первая решка заняла 1 из 6 мест, вторая 1 из 5 оставшихся, третья 1 из 4 оставшихся, т.е. всего $$6\cdot5\cdot4=120$$ вариантов. Но тут каждая комбинация учтена 6 раз (3 разных нуля друг относительно друга располагаются $$3!=6$$ способами). Т.е. мы учли $$O_1O_2O_3PPP;O_2O_1O_3PPP$$ и т.д. как разные комбинации. Потому реальных различных комбинаций $$\frac{120}{6}=20$$ штук. При этом ОООРРР всего одна:
$$P(A)=\frac{1}{20}=0,05$$
Задание 11
$$y=(\sqrt{x^3-3x+11})'=\frac{1}{2\sqrt{x^3-3x+11}}\cdot(x^3-3x+11)'=0$$
Получим:
$$(x^3-3x+11)'=0\Leftrightarrow 3x^2-3=0\Rightarrow x=\pm1$$
При $$x=0: 3\cdot0^2-3=-3<0$$
При $$x=\pm2: 3\cdot(\pm2)^2-3=9>0$$
Т.е. $$x=-1\rightarrow max; x=1\rightarrow min$$
Поэтому $$y_{min}=y(-2)$$ или $$y(1).$$
$$y(-2)=\sqrt{8+6+11}=\sqrt{25}=5$$
$$y(1)=\sqrt{1-3+11}=\sqrt{9}=3$$