378 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.

$$\sqrt{\frac{32-x}{-x}}=3\Leftrightarrow \frac{32-x}{-x}=9\Leftrightarrow -9x=32-x\Leftrightarrow -8x=32\Rightarrow x=-4$$

Сначала найдем вероятность, что кофе закончится хотя бы в одном автомате. Имеем два события:

А: кофе закончилось в первом автомате;

B: кофе закончилось во втором автомате;

AB: кофе закончилось в обоих автоматах.

Вероятность этих событий равна $$P(A)=P(B)=0,8, P(AB)=0,72.$$ Вероятность суммы событий $$A+B$$ (кофе закончилось или в первом или во втором автомате или в обоих вместе), равна:

$$P(A+B)=P(A)+P(B)-P(AB)$$

$$P(A+B)=0,8+0,8-0,72=0,88$$

Тогда обратная вероятность

$$1-P(A+B)=1-0,88=0,12$$

будет означать, что кофе осталось в обоих автоматах.

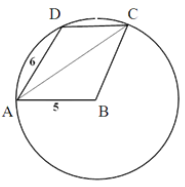
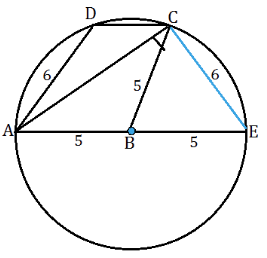
В - центр окружности. АВ - радиус. Продолжим его до пересечения с окружностью в точке Е. 

АЕ-диаметр. Соединим С и Е. 

ADCЕ- трапеция, т.к. DC параллельна AE.

Эта трапеция - вписанная, а вписать можно только равнобедренную трапецию. Это следует из свойства вписанного четырехугольника (сумма противоположных углов равна 180º, это и  свойство равнобедренной трапеции).

⇒ СЕ=АD=6

АЕ=2r=10.

Угол АСЕ - вписанный, опирается на диаметр ⇒ равен 90º.

В треугольнике АСЕ  гипотенуза равна 10, один катет = 6, следовательно, он - египетский, второй катет АС=8 (можно найти по теореме Пифагора).

АС=8

$$\frac{5\sin(3\pi-a)+7\cos(\frac{\pi}{2}-a)}{2\sin(\pi-a)}=\frac{5\sin\alpha+7\sin\alpha}{2\sin\alpha}=\frac{12}{2}=6$$

Сечением будет треугольник $$BA_1C_1.$$

Из $$\Delta BB_1A_1:$$

$$BA_1=\sqrt{BB_1^2+B_1A_1^2}=\sqrt{17}$$

Из $$\Delta BB_1C_1:$$

$$BC_1=\sqrt{17}$$

Из $$\Delta A_1B_1C_1:$$

$$A_1C_1=\sqrt{18}$$

$$P_{ABC}=\frac{\sqrt{17}+\sqrt{17}+\sqrt{18}}{2}=\sqrt{17}+\frac{\sqrt{18}}{2}$$

$$S_{BA_1C_1}=\sqrt{(\sqrt{17}+\frac{\sqrt{18}}{2})\cdot\frac{\sqrt{18}}{2}\cdot\frac{\sqrt{18}}{2}\cdot(\sqrt{17}-\frac{\sqrt{18}}{2})}=$$

$$=\sqrt{(17-\frac{18}{4})\cdot\frac{18}{4}}=\sqrt{\frac{50}{4}\cdot\frac{18}{4}}=\frac{30}{4}=7,5$$

$$F(10)-F(3)$$ равно площади трапеции, ограниченной графиком функции, осью $$Ox$$ и прямыми вида $$x=3$$ и $$x=10.$$

$$S=\frac{3+7}{2}\cdot5=25.$$

В баке останется четверть первоначального объeма воды $$\Rightarrow H(t)=\frac{H_0}{4}=\frac{20}{4}=5$$

$$5=20-\sqrt{2\cdot10\cdot20}\cdot\frac{1}{500}t+5\cdot(\frac{1}{500})^2\cdot t^2$$

$$5=20-20\cdot\frac{1}{500}t+\frac{5t^2}{500^2}$$

$$5=20-\frac{1}{25}t+\frac{5t^2}{500^2}$$

$$125\cdot500^2=500^3-500^2t+125t^2$$

$$125t^2-500^2t-125\cdot500^2+500^3=0$$

$$125(t^2-500^2)-500^2\cdot(t-500)=0$$

$$125(t-500)(t+500)-500^2(t-500)=0$$

$$(t-500)(125(t+500)-500^2)=0$$

$$(t-500)(125t+62500-500^2)=0$$

$$t-500=0 и 125t+62500-500^2=0$$

$$t=500$$ и $$t=1500$$

Через 500 минуту в банке останется четверть первоначального объема воды, число 1500 не имеет физического смысла

Минутная стрелка проходит круг за 60 минут.

Пусть круг 1. Тогда скорость минутной $$\frac{1}{60}$$ круга в минуту, часовой $$\frac{1}{720}$$ круга в минуту.

Разность скоростей $$\frac{1}{60}-\frac{1}{720}=\frac{11}{720}$$ круга в минуту.

Изначально от минутной до часовой $$\frac{35}{60}+\frac{10}{60}+\frac{25}{60}\cdot\frac{1}{12}=\frac{565}{720}=\frac{113}{144}$$ круга.

($$\frac{25}{60}\cdot\frac{1}{12}$$ - это часть круга, которую прошла часовая стрелка за 35 минут от отметки 2 часа)

Именно на столько $$+8$$ полных кругов должна пройти больше минутная, чтобы поравняться 9 раз:

$$\frac{\frac{565}{720}+8}{\frac{11}{720}}=\frac{565+8\cdot720}{720}\cdot\frac{720}{11}=\frac{6325}{11}=575$$

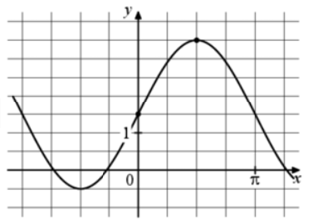
Точка $$(0;1,5)$$ принадлежит графику функции. Тогда:

$$1,5=a\sin0+b$$

$$b=1,5$$

Точка $$(\frac{\pi}{2};3,5)$$ принадлежит графику функции. Тогда:

$$3,5=a\sin\frac{\pi}{2}+1,5$$

$$a=2$$

$$\frac{C^5_10}{C^4_10}=\frac{10!}{(10-5)!\cdot5!}\cdot\frac{(10-4)!\cdot4!}{10!}=\frac{6!\cdot4!}{5!\cdot5!}=\frac{6}{5}=1,2$$

$$y'=6+6\sin2x$$

$$6\sin2x=-6$$

$$\sin2x=-1$$

$$x=0,75 $$

$$y(\frac{\pi}{2})=\frac{6\pi}{2}-3\cos\frac{2\pi}{2}-3\pi=3$$

$$y(\frac{3\pi}{2})=6\pi-3\cos3\pi-3\pi=3\pi+3$$

$$min=3$$