ОГЭ математика 2023. Разбор варианта Алекса Ларина № 332.
Больше разборов на моем ютуб-канале
Задания 1-5
 В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы (см. рис. выше). Земледельческие террасы - это горизонтальные площадки, напоминающие ступени. Во время дождя вода стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье - для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует тяжёлого ручного труда.
Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка равна 40 м, а верхняя точка находится на высоте 12 м от подножия.
1. Земледелец на расчищенном склоне холма (ещё не террасированном) выращивал мускатный орех. Какова была площадь (в м2), отведённая под посевы?
2. Затем земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла наклона, умноженный на 100%). Сколько процентов составляет уклон? Ответ округлите до десятых.
В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы (см. рис. выше). Земледельческие террасы - это горизонтальные площадки, напоминающие ступени. Во время дождя вода стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье - для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует тяжёлого ручного труда.
Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка равна 40 м, а верхняя точка находится на высоте 12 м от подножия.
1. Земледелец на расчищенном склоне холма (ещё не террасированном) выращивал мускатный орех. Какова была площадь (в м2), отведённая под посевы?
2. Затем земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла наклона, умноженный на 100%). Сколько процентов составляет уклон? Ответ округлите до десятых.
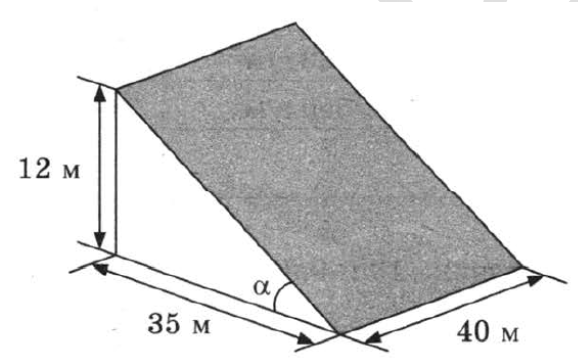 3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
4. Земледелец получает 650 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 16% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
5. В таблице дана урожайность культур, которые может засеять земледелец на своём террасированном участке. За год обычно собирается два урожая: летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
4. Земледелец получает 650 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 16% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
5. В таблице дана урожайность культур, которые может засеять земледелец на своём террасированном участке. За год обычно собирается два урожая: летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
| Урожай |
Урожайность риса (г/м2) |
Урожайность кукурузы (г/м2) |
Урожайность пшена (г/м2) |
|---|---|---|---|
| Первый (июнь) | |||
| Второй (сентябрь) |
1.
$$S_{посевов}=АВ\cdot AD$$
$$\Delta ABC$$ прямоугольный
по т. Пифагора $$АВ² = АС² + ВС²$$
$$АВ² = 12² + 35²$$
$$АВ² = 144 + 1225$$
$$АВ² = 1369$$
$$АВ = 37$$
$$S_{посевов}=АВ\cdot AD=37\cdot40=1480$$
2.
Тангенс угла = отношение противолежащего катета к прилежащему
Тангенс угла склона $$= \frac{12}{35}\approx0,343$$
Угол склона = Тангенс угла склона $$\cdot$$ 100% $$= 0,343\cdot100 = 34,3$$
3.
$$S_{посевов}=АВ\cdot AD$$
$$\Delta ABC$$ прямоугольный
по т. Пифагора $$АВ² = АС² + ВС²$$
$$АВ² = 12² + 35²$$
$$АВ² = 144 + 1225$$
$$АВ² = 1369$$
$$АВ = 37$$
$$S_{посевов}=АВ\cdot AD=37\cdot40=1480$$
Если земледелец устроил террасы, $$S_{посевов}=АС\cdot AD=35\cdot40=1400$$
1480 - 100%
1400 - x%
$$x=1400\cdot\frac{100}{1480}$$
$$x\approx94,6$$
100% - 94,6% = 5,4%
4.
Если земледелец устроил террасы, $$S_{посевов}=АС\cdot AD=35\cdot40=1400$$
Получит бурого риса $$1400\cdot650$$ гр $$=910000$$ гр $$=910$$ кг
Теряется при шлифовке 16%, значит останется (100%-16%=84%) риса
910 - 100%
х - 84%
$$х=910\cdot\frac{84}{100}$$
$$х=764,4$$
5.
Если земледелец устроил террасы, $$S_{посевов}=АС\cdot AD=35\cdot40=1400$$
Возможны варианты:
Рис + Рис $$1400\cdot(650+550)$$
Рис + Пшено $$1400\cdot(650+600)$$
Кукуруза + Рис $$1400\cdot(800+550)$$
Кукуруза + Пшено $$1400\cdot(800+600)$$
Суммируем числа в скобках. Наибольшее получается Кукуруза + Рис
Кукуруза + Рис $$1400\cdot(800+600)=1960000$$ гр $$=1960$$ кг
Задание 6
$$\frac{1}{5}-\frac{27}{20}=\frac{4-27}{20}=\frac{-23}{20}=\frac{-115}{100}=-1,15$$
Задание 7
Пусть $$a=0,5; b=0,5.$$
1) $$\frac{a}{b}=\frac{-0,5}{0,5}=-1<0$$ - нет
2) $$b-a=0,5-(-0,5)=1<-1$$ - нет
3) $$a+b=-0,5+0,5=0>1$$ - нет
4) $$ab=-0,5\cdot0,5=-0,25>-1$$ - да
Задание 8
$$\frac{a^2+7a}{a^2+14a+49}=\frac{a(a+7)}{(a+7)^2}=\frac{a}{a+7}=\frac{-2}{-2+7}=-0,4$$
Задание 11
А) $$f(x+2)=x+2+\frac{3}{x+2}$$
$$x+2+\frac{3}{x+2}=x+\frac{3}{x}\Leftrightarrow\frac{3}{x}-\frac{3}{x+2}=2\Rightarrow 3x+6-3x=2x^2+4x\Rightarrow$$
$$\Rightarrow2x^2+4x-6=0\Leftrightarrow x^2+2x-3=0\Rightarrow\left[\begin{matrix} x=-3\\ x=1 \end{matrix}\right.\Rightarrow x=3.$$
Б) $$f(x+1)=x+1+\frac{3}{x+1}\Rightarrow x+2+\frac{3}{x+2}=x+1+\frac{3}{x+1}\Rightarrow \frac{3}{x+1}-\frac{3}{x+2}=1\Rightarrow$$
$$\Rightarrow3x+6-3x-3=x^2+3x+2\Rightarrow x^2+3x-1=0\Rightarrow D=9+4=(\sqrt{13})^2\Rightarrow$$
$$\Rightarrow x=\frac{-3\pm\sqrt{13}}{2}\Rightarrow 1.$$
В) Проверим $$x=\frac{7}{2}: f(\frac{7}{2}-5)=f(2-\frac{7}{2})\Rightarrow f(-1,5)=f(-1,5)\Rightarrow x=4.$$
Получим: $$3142.$$
Задание 12
Задание 13
1) $$x^25\leq0\Rightarrow x\in\varnothing$$ - нет
2) $$x^2-25\leq0\Rightarrow x\in [-5;5]$$ - да
3) $$x^2+25\geq0\Rightarrow x\in R$$ - нет
4) $$x^2-25\geq0\Rightarrow x\in (-\infty;-5]\cup[5;+\infty)$$ - нет
Задание 14
Ежемесячные выплаты составляют арифметическую прогрессию с первым членом $$\frac{100}{n}$$ и разностью 5. Тогда за последний месяц клиент выплатил банку $$\frac{100}{n}+5(n-1)$$ руб., что составляет 55 руб. Решим уравнение:
$$\frac{100}{n}+5(n-1)=55\Leftrightarrow 100+5n(n-1)=55n\Leftrightarrow$$
$$\Leftrightarrow 5n^2-60n+100=0\Leftrightarrow n^2-12n+20=0\Leftrightarrow\left[\begin{matrix} n=10\\ n=2 \end{matrix}\right.$$
Поскольку срок кредитования превышал полгода, кредит был возвращен банку за 10 месяцев.
Задание 15
$$\angle AOD=180^{\circ}-\angle DOB=180^{\circ}-64^{\circ}=116^{\circ}$$
$$\angle AOK=\frac{\angle AOD}{2}=\frac{116^{\circ}}{2}=58^{\circ}$$
Задание 16
$$OA=OB$$ - радиусы $$\Rightarrow \angle OAB=\angle OBA=\frac{180^{\circ}-60^{\circ}}{2}=60^{\circ}\Rightarrow \Delta AOB$$ - равносторонний $$\Rightarrow OA=4.$$
Задание 17
Пусть R - радиус и D - диаметр окружности, a - сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата:
$$S=D^2=(2R)^2=(2\cdot25)^2=2500$$
Задание 18
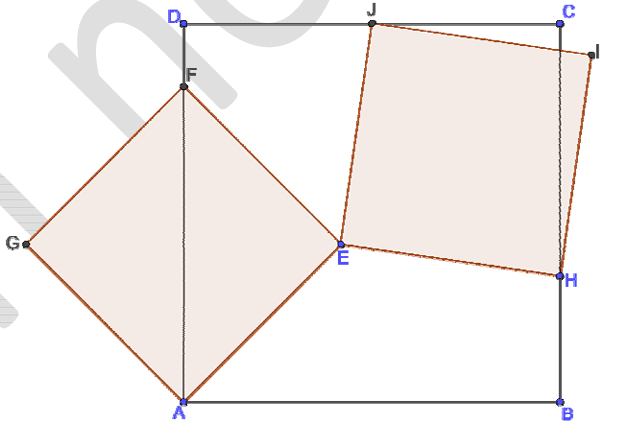
Пусть $$EK\perp AD; EN\perp CB; EM\perp DC.$$ Тогда:
$$\Delta EMJ=\Delta ENH$$ (по гипотенузе и острому углу) $$\Rightarrow MJ=NH=x.$$
$$EK=KA=\frac{AF}{2}=\frac{4\sqrt{2}\cdot\sqrt{2}}{2}=4=NB=DM.$$
Тогда $$DJ+BH=DM+MJ+BN-NH=4+x-x+4=8.$$
Задание 19
1) неверно, диагонали ромба не равны
2) неверно, отношение площадей равно квадрату коэффициента подобия.
3) верно.
Задание 20
$$a^8-a^4-2a^2-1=a^8-(a^2+2a^2+1)=a^8-(a^2+1)^2=$$
$$(a^4)^2-(a^2+1)^2=(a^4-(a^2+1))(a^4+(a^2+1))=(a^4-a^2-1)(a^4+a^2+1)=$$
$$=(a^4-a^2-1)(a^4+2a^2+1-a^2)=(a^4-a^2-1)((a^2+1)^2-a^2)=$$
$$=(a^4-a^2-1)(a^2+1-a)(a^2+1+a)$$
Задание 21
Если верно первое утверждение, то верно и второе. Это противоречит тому, что верно только одно из двух данных утверждений. Следовательно, верно второе утверждение, а первое неверно. Получаем, что $$37\leq a<38.$$ Этому неравенству удовлетворяет единственное целое число: $$a=37.$$
Задание 22
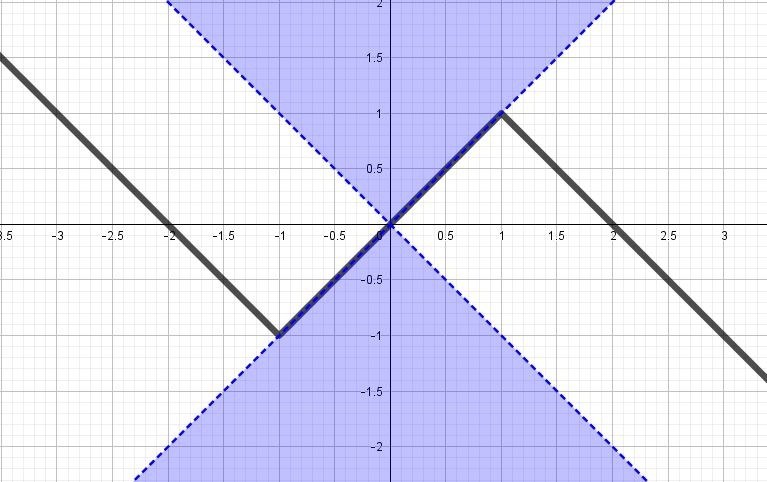
$$y=|x+1|-|x-1|-x$$
$$y=\left\{\begin{matrix} -x-1-(-x+1)-x,x\leq-1\\ x+1-(-x+1)-x,x\in(-1;1]\\ x+1-(x-1)-x,x>1 \end{matrix}\right.\Leftrightarrow y=\left\{\begin{matrix} -x-2,x\leq-1\\ x,x\in(-1;1]\\ -x+2,x>1 \end{matrix}\right.\Leftrightarrow$$
Ровно одну будет иметь при $$a>1$$ и $$a\in(-\infty;-1],$$ т.е. $$a\in (-\infty;-1]\cup(1;+\infty)$$
(на рисунке выделим зоны, где должен располагаться $$y=ax$$)
Задание 23
Треугольник $$CFD:$$
$$h=a\sin60=\frac{a\sqrt{3}}{2}$$
$$h^2=\frac{3a^2}{4}$$
Треугольник $$BEA:$$
$$h^2=AB^2-\frac{a^2}{4}$$
$$AB^2-\frac{a^2}{4}=\frac{3a^2}{4}$$
$$AB^2=\frac{3a^2}{4}+\frac{a^2}{4}$$
$$AB^2=a^2$$
$$AB=a$$
$$a=1$$
$$h=\frac{a\sqrt{3}}{2}=1\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$$
$$S=\frac{1+2}{2}\cdot\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}$$
Задание 24
$$\Delta BED$$ равнобедренный (углы при основании равны) $$\Rightarrow ВЕ = BD$$
$$\Delta AEB = \Delta CDB (\angle E = \angle D, AE=DC, BE=BD)\Rightarrow AB = BC\Rightarrow \Delta ABC$$ равнобедренный
Задание 25
Введём обозначения, как показано на рисунке. Поскольку HG||AC и HE||BD, получаем, что HKOL — параллелограмм, следовательно, углы KHL и KOL равны. Рассмотрим треугольники ABC и EBF, угол EBF — общий, углы BEF и BAC равны как соответственные при параллельных прямых, углы BFE и BCA — аналогично, следовательно, треугольники ABC и BEF подобны по двум углам. Откуда $$\frac{EF}{AC}=\frac{BE}{AB}.$$ Аналогично подобны треугольники ABD и AEH, откуда $$\frac{HE}{BD}=\frac{AE}{AB}.$$ Пусть сторона ромба равна a, а длина короткой диагонали равна d. Сложим два полученных уравнения:
$$\frac{EF}{AC}+\frac{HE}{BD}=\frac{AE}{AB}+\frac{BE}{AB}\Leftrightarrow\frac{a}{d}+\frac{a}{9d}=\frac{AE+EB}{AB}\Leftrightarrow$$
$$\Leftrightarrow\frac{9a+a}{9d}=\frac{AB}{AB}\Leftrightarrow9d=10a\Leftrightarrow a=\frac{9d}{10}$$
Площадь ромба можно найти как произведение сторон на синус угла между ними: $$S_{HEFG}=a^2\sin\angle KHL.$$ Площадь параллелограмма можно найти как половину произведения диагоналей на синус угла между ними: $$S_{ABC}=\frac{1}{2}\cdot AC\cdot BD\cdot\sin\angle KOL=\frac{1}{2}\cdot9d\cdot\sin\angle KOL.$$ Найдём отношение площадей ромба и параллелограмма:
$$\frac{S_{HEFG}}{S_{ABCD}}=\frac{a^2\sin\angle KHL}{\frac{1}{2}\cdot d\cdot 9d\cdot\sin\angle KOL}=\frac{a^2}{4,5d^2}=\frac{d^2\cdot\frac{9^2}{10^2}}{4,5d^2}=\frac{9}{50}=0,18$$