ОГЭ математика 2019. Разбор варианта Алекса Ларина № 188.
Решаем ОГЭ 188 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №188 (alexlarin.com)
Решаем ОГЭ 188 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №188 (alexlarin.com)
Задание 1
Найдите значение выражения: $$(\frac{4}{9}-\frac{5}{12}):(\frac{3}{8}-\frac{4}{9})$$
$$(\frac{4}{9}-\frac{5}{12}):(\frac{3}{8}-\frac{4}{9})=$$$$\frac{4*4-5*3}{36}:\frac{3*9-4*8}{72}=$$$$\frac{1}{36}*\frac{72}{-5}=-\frac{2}{5}=-0,4$$
Задание 2
Расстояние от Нептуна – одной из планет Солнечной системы – до Солнца равно 4450 млн км. Как эта величина записывается в стандартном виде?
Варианты ответа:
- $$4.450*10^{6}$$
- $$4.450*10^{7}$$
- $$4.450*10^{8}$$
- $$4.450*10^{9}$$
Стандартный вид числа : $$a*10^{n}$$, где $$1\leq a <10, n \in N$$. Учтем, что 1 млн = $$10^{6}$$. Тогда 4450 млн. км. = $$4,450*10^{3}*10^{6}=4,45*10^{9}$$ км. Данный ответ соответствует 4 варианту.
Задание 3
На координатной прямой отмечено число а. Какое из утверждения для этого числа верно?
- $$a-5<0$$
- $$a-7>0$$
- $$5-a>0$$
- $$8-a<0$$
Число а располагается между 7 и 8. Пусть а=7,5. Проверим истинность представленных вариантов:
- $$a-5<0\Leftrightarrow$$$$7,5-5<0\Leftrightarrow$$$$2,5<0$$ - неверно
- $$a-7>0\Leftrightarrow$$$$7,5-7>0\Leftrightarrow$$$$0,5>0$$ - верно
- $$5-a>0\Leftrightarrow$$$$5-7,5>0\Leftrightarrow$$$$-2,5>0$$ - неверно
- $$8-a<0\Leftrightarrow$$$$8-7,5<0\Leftrightarrow$$$$0,5<0$$ - неверно
Верным является только 2 вариант ответа
Задание 4
Найдите значение выражения $$\sqrt{5*90}\sqrt{50}$$
$$\sqrt{5*90}\sqrt{50}=$$$$\sqrt{5*9*10*5*10}=$$$$\sqrt{3^{2}*5^{2}*10^{2}}=$$$$3*5*10=150$$
Задание 5
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,2 В до 0,8 В.
1,2 В было в 9 часов, 0,8 В было в 19 часов, следовательно, с 1,2 В до 0,8 В напряжение упадет за 19-9=10 часов
Задание 6
Решите уравнение $$4x+5=-9(8-9x)$$
$$4x+5=-9(8-9x)\Leftrightarrow$$$$4x+5=-72+81x\Leftrightarrow$$$$4x-81x=-72-5\Leftrightarrow$$$$-77x=-77|:(-77)\Leftrightarrow$$$$x=1$$
Задание 7
В 6 классе учится 10 мальчиков, остальные ученики - девочки. Контрольную работу успешно написали 60% мальчиков и 90% девочек. Сколько человек учится в 6 классе, если всего контрольную работу успешно написали 24 человека?
1. 60% мальчиков успешно написали, следовательно, 10*0,6=6 мальчиков
2. 24-6=18 девочек успешно написали, что составляет 90 % от общего числа девочек, тогда:
3. Тогда всего детей 20+10=30 человек
Задание 8
На диаграммах показано содержание питательных веществ в сухарях, твороге, сливочном мороженном и сгущенном молоке. Определите по диаграммам, в каком продукте содержание углеводов наибольшее
*к прочему относятся вода, витамины и минеральные вещества
Варианты ответа
- сухари
- творог
- мороженое
- сгущённое молоко
Необходимо выбрать круг, в котором площадь сегмента, характеризующего углеводы, наибольшая. В данном случае это первый вариант - сухари
Задание 9
В среднем на 147 исправных карманных фонариков, поступивших в продажу, приходится три неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен
Если на 147 исправных фонарика 3 неисправных, тогда всего фонариков : 147+3=150 фонариков. Тогда вероятность выбрать исправный фонарик: $$P=\frac{147}{150}=0,98$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
- $$-\frac{2}{x}$$
- $$x^{2}-2$$
- $$2x$$
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
В пункте А представлена квадратичная функция вида $$y=ax^{2}+b$$, ей соответствует 2 вариант ответа В пункте Б представлена линейная функция вида $$y=kx$$, ей соответствует 3 вариант ответа В пункте В представлена обратная пропорциональность вида $$y=\frac{k}{x}$$, ей соответствует 1 вариант ответа
Задание 11
Даны двадцать чисел, первое из которых равно 10, а каждое следующее больше предыдущего на 4. Найти пятнадцатое из данных чисел.
В данном случае дана арифметическая прогрессия, первый член которой $$a_{1}=10$$, разность $$d=4$$. Необходимо найти $$a_{15}$$. $$a_{n}=a_{1}+d(n-1)$$, следовательно, $$a_{15}=10+4(15-1)=66$$
Задание 12
Найдите значение выражения $$(a-1):\frac{2a-a^{2}-1}{a+1}$$, при $$a=-24$$
$$(a-1):\frac{2a-a^{2}-1}{a+1}=$$$$(a-1)*\frac{a+1}{-(-2a+a^{2}+1)}=$$$$\frac{(a-1)*(a+1)}{-(a-1)^{2}}=$$$$\frac{a+1}{-(a-1)}=$$$$\frac{-24+1}{-(-24-1)}=-\frac{23}{25}=-0,92$$
Задание 13
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой F=1,8C+32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует -8 градусам по шкале Цельсия?
Подставим в формулу известные значения: $$F=1,8C+32=$$$$ F=1,8*(-8)+32=$$$$ F=-14,4+32=17,6$$
Задание 14
Решите неравенство $$64-x^{2}<0$$
Варианты ответа:
- $$(--\infty ;+\infty )$$
- $$(-\infty ;-8)\cup (8;+\infty)$$
- $$(-8;8)$$
- нет решений
Разложим выражение слева на множители: $$(8-x)(8+x)<0$$. Отметим на координатной прямой точки (пустые, так как неравенство строгое), когда выражение слева равно 0 и расставим знаки значений, которые принимает выражение на полученных промежутках:
Нам необходимы значения меньшие, чем ноль, следовательно, $$x\in(-\infty ;-8)\cup (8;+\infty)$$, что соответствует 2 варианту ответа
Задание 15
Какой угол (в градусах) описывает минутная стрелка за 27 минут?
Вся окружность составляет 360 градусов или 60 минут, тогда 1 минута составляет $$\frac{360}{60}=6$$ градусов, следовательно, 27 минут составляют $$27*6=162$$ градуса
Задание 16
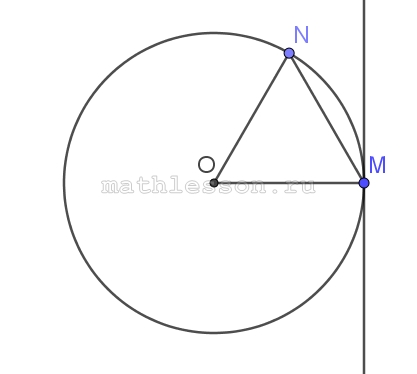
Прямая касается окружности в точке M . Точка O — центр окружности. Хорда MN образует с касательной угол, равный 22°. Найдите величину угла ONM. Ответ дайте в градусах
- OM перпендикулярен касательной (свойство радиуса, проведенного в точку качсания)
- ON=OM (радиусы), тогда $$\angle ONM=\angle OMN$$
- $$\angle OMN=90-22=68$$
Задание 17
Найдите периметр прямоугольника, если в него вписана окружность радиуса 10.
Если в прямоугольник вписана окружность, то данный прямоугольник является квадратом (так как сумма противоположных сторон равна) Радиус вписанной окружности в квадрат равен половине стороны квадрата, то есть сторона квадрата тогда 20 Периметр есть сумма длин всех сторон: $$P=20*4=80$$
Задание 18
Боковая сторона равнобедренного треугольника равна 26, а основание равно 12. Найдите площадь этого треугольника
Воспользуемся формулой Герона для вычисления площади треугольника. Найдем полупериметр: $$p=\frac{26+26+12}{2}=32$$. Тогда площадь треугольника равна: $$S=\sqrt{32(32-62)(32-26)(32-12)}=48\sqrt{10}$$
Задание 19
В остроугольном треугольнике ABC высота AH равна $$20\sqrt{3}$$ , а сторона AB равна 40. Найдите $$\cos B$$.
Из треугольника ABH найдем синус угла B: $$\sin B=\frac{AH}{AB}=\frac{\sqrt{3}}{2}$$ Найдем косинус угла B по основному тригонометрическому тождеству: $$\cos B=\sqrt{1-\sin^{2} B}=\sqrt{1-\frac{3}{4}}=\frac{1}{2}$$
Задание 20
Какие из следующих утверждений верны?
- Площадь параллелограмма равна произведению его смежных сторон.
- Площадь прямоугольника равна произведению его смежных сторон.
- Площадь ромба равна произведению его смежных сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
- Площадь параллелограмма равна произведению его смежных сторон - неверно, произведению смежных сторон на синус угла между ними
- Площадь прямоугольника равна произведению его смежных сторон - верно
- Площадь ромба равна произведению его смежных сторон - ромб - тот же параллелограмм, следовательно, неверно
Задание 21
Упростите выражение: $$\frac{a-c}{a^{2}+ac+c^{2}}\cdot \frac{a^{3}-c^{3}}{a^{2}b-bc^{2}}\cdot(1+\frac{c}{a-c}-\frac{1+c}{c}):\frac{c(1+c)-a}{bc}$$
Выполним данное задание по действиям:
- $$\frac{a-c}{a^{2}+ac+c^{2}}\cdot \frac{a^{3}-c^{3}}{a^{2}b-bc^{2}}=$$$$\frac{a-c}{a^{2}+ac+c^{2}}\cdot \frac{(a-c)(a^{2}+ac+c^{2})}{b(a-c)(a+c)}$$$$=\frac{a-c}{b(a+c)}$$
- $$1+\frac{c}{a-c}-\frac{1+c}{c}=$$$$\frac{ac-c^{2}+c^{2}-a-ac+c+c^{2}}{c(a-c)}=$$$$\frac{c+c^{2}-a}{c(a-c)}$$
- $$\frac{a-c}{b(a+c)}*\frac{c+c^{2}-a}{c(a-c)}*\frac{bc}{c(1+c)-a}=\frac{1}{(a+c)}$$
Задание 22
Бригада лесорубов должна была за несколько дней заготовить 216 м3 древесины. Первые три дня она выполняла установленную норму, а затем – каждый день заготавливала на 8 м3 больше плана, поэтому за день до срока было заготовлено 232 м3 древесины. Определите плановую дневную норму бригады.
Пусть планировалось добывать х кубических метров в день, в течении у дней. Тогда получаем $$xy=216$$. Но сначала три дня добывали по норме, а потом оставшиеся дни без одного (так как за день до нормы закончили) добывали на 8 больше, то есть $$3x+(y-4)(x+8)=232$$. (y-4 - от того, что три дня уже работали, плюс закончили на 1 день раньше):
$$\left\{\begin{matrix}xy=216\\3x+(y-4)(x+8)=232\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}xy=216\\3x+xy+8y-4x-32=232\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}xy=216\\8y-x+xy-32=23\end{matrix}\right. $$
Подставим вместо xy число 216:
$$8y-x+216-32=232\Leftrightarrow$$$$8y-x=48\Leftrightarrow$$$$x=8y-48$$
Подставим в первое уравнение системы:
$$(8y-48)y=216|:8\Leftrightarrow$$$$y^{2}-6y-27=0$$.
Тогда корни данного уравнения 9 и -3. Количество дней не может быть отрицательным, следовательно, $$y=9$$. Найдем х: $$x=8-9-48=24$$
Задание 23
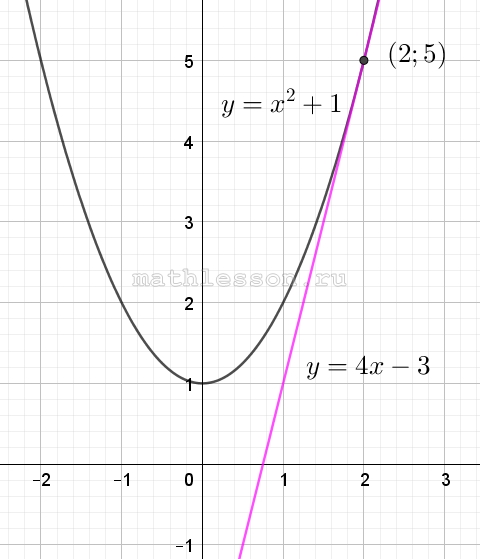
Известно, что графики функций y=x2 +p и y=4x−3 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат
- Так как графики имеют одну точку пересечения, то уравнение : $$x^{2}-p=4x-3$$ должно иметь один корень, то есть дискриминант равен 0:
- $$x^{2}-4x+p+3=0$$ $$D=16-4(p+3)=16-4p+12=4-4p=0$$
- Тогда $$p=1$$.
- Найдем абсциссу точки пересечения: $$x_{0}=-\frac{-4}{2}=2$$.
- Найдем ординату (подставим в линейное уравнение): $$y=4*2-3=5$$. То есть точка пересечения будет с координатами (2;5).
- Построим графики функций:
Задание 24
Диагональ равнобедренной трапеции делит пополам угол при её основании. Найдите большее основание трапеции, если её меньшее основание равно 5 см, а высота - 4,8 см.
- $$\angle BAC=\angle CAD$$ (AC - биссектрисса)
- $$\angle CAD=\angle BCA$$ (накрест лежащие при параллельных), следовательно треугольник ABC - равнобедренный и $$AB=BC=CD=5$$
- Проведем перпендикуляры BM и CH к AD. Из треугольника CHD: $$HD=\sqrt{CD^{2}-CH^{2}}=\sqrt{5^{2}-4,8^{2}}=1,4$$
- $$AM=HD=1,4$$, тогда $$AD=5+1,4*2=7,8$$
Задание 25
Середины сторон параллелограмма являются вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
- $$AB=CD, BC=AD$$ так как дан параллелограмм. Следовательно, $$AM=MB=DL=LC$$, и $$AK=KD=BN=NC$$.
- $$\angle A+\angle D=180$$. Но $$MK=NK$$, следовательно, треугольники AMK и KLD равны по трем сторонам и $$\angle A=\angle D$$. Так как они в сумме дают 180, то какждый из них по 90, тогда ABCD - прямоугольник.
Задание 26
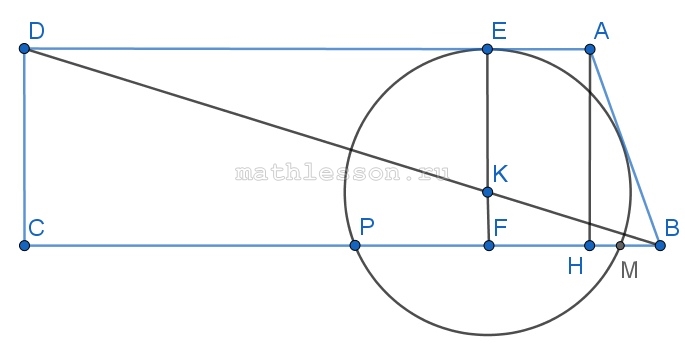
На диагонали BD прямоугольной трапеции ABCD с прямым углом ADС и основаниями ВС и АD, взята точка К так, что ВК : КD = 1 : 3. Окружность с центром в точке К касается прямой АD и пересекает прямую ВС в точках Р и М. Найдите длину стороны АВ, если ВС = 9, АD = 8, РМ = 4.
- Пусть Е - точка касания, проведем перпендикуляр через E и K (свойство радиуса в точку касания). Пусть EK пересекает CB в точке F
- Так как $$EF\perp PM$$, то $$FP=FM$$ (из равенства треугольников KFP и KFM). Так же $$KE=KP=K=R$$ (радиусы)
- Треугольники KED и KFB подобный (так как дана трапеция), тогда $$\frac{KF}{KE}=\frac{KB}{KD}=\frac{1}{3}$$, тогда $$KF=\frac{1}{3}KE=\frac{R}{3}$$
- из треугольника PKF: $$KP^{2}=PF^{2}+KF^{2}$$ или $$R^{2}=\frac{1}{9}R^{2}+4$$. Отсюда $$R=\frac{3}{\sqrt{2}}$$
- Опустим $$AH\perp BC$$ (AH пересекает BC в точке H). Тогда $$AH=EK+KF=\frac{4}{3}R=2\sqrt{2}$$, $$HB=BC-AD=1$$
- Из треугольника AHB: $$AB=\sqrt{1^{2}+(2\sqrt{2})^{2}}=3$$