ОГЭ математика 2018. Разбор варианта Алекса Ларина № 178.
Решаем ОГЭ 178 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №178 (alexlarin.com)
Решаем ОГЭ 178 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №178 (alexlarin.com)
Задание 1
Найдите значение выражения $$15\cdot(\frac{1}{5})^{2}-3\frac{1}{5}$$
$$15\cdot(\frac{1}{5})^{2}-3\frac{1}{5}=$$ $$15\cdot\frac{1}{25}-\frac{16}{5}=\frac{15}{25}-\frac{16}{5}=$$ $$\frac{3}{5}-\frac{16}{5}=-\frac{13}{5}=-2,6$$
Задание 2
В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40-97 | 70-154 | 60-102 |
| Белки | 36-87 | 65-117 | 58-87 |
| Углеводы | 170-420 | 257-586 | |
Какой вывод о суточном потреблении жиров, белков и углеводов 12-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 43 г жиров, 55 г белков и 160 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
Задание 3
Одно из чисел $$\sqrt{17}$$, $$\sqrt{22}$$, $$\sqrt{28}$$, $$\sqrt{32}$$ отмечено на прямой, точкой А. Какое это число?
Варианты ответа:
1) $$\sqrt{17}$$,
2) $$\sqrt{22}$$,
3) $$\sqrt{28}$$,
4) $$\sqrt{32}$$.
Число А больше 4,но меньше 5, т.е. $$\sqrt{16}<A<\sqrt{25}$$, ближе к 4, т.е. $$\sqrt{17}$$
Задание 4
Сколько целых чисел расположено между числами $$-\sqrt{80}$$ и $$-\sqrt{8}$$
$$-\sqrt{80}>-\sqrt{81}=-9$$
$$-\sqrt{8}<-\sqrt{4}=-2$$
$$-9<N<-2$$ $$\Rightarrow$$ $$-8;-7;-6;-5;-4;-3$$
Задание 5
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость в километрах в час, по вертикальной — тормозной путь в метрах. Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 60 км/ч. Ответ дайте в метрах.
Задание 8
Завуч подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на диаграмме.
Какие из утверждений относительно результатов контрольной работы верны, если всего в школе 120 девятиклассников?
1. Более половины девятиклассников получили отметку «3».
2. Около половины девятиклассников отсутствовали на контрольной работе.
3. Отметку «4» или «5» получила примерно треть девятиклассников.
4. Отметку «3», «4» или «5» получили менее 100 учащихся
Задание 9
В среднем из каждых 80 поступивших в продажу аккумуляторов 68 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.
$$80-68=12$$ - незаряжен; $$p=\frac{12}{80}=0,15$$
Задание 11
Найдите сумму пятидесяти первых членов арифметической прогрессии, заданной формулой $$a_{n}=0,5n-14$$.
$$a_{1}=0,5-14=-13,5$$; $$a_{2}=1-14=-13$$; $$d=a_{2}-a_{1}=-13-(-13,5)=0,5$$; $$S_{50}=\frac{2\cdot(-13,5)+0,5\cdot(50-1)}{2}\cdot50=(-27+24,5)\cdot25=-62,5$$
Задание 12
Найдите значение выражения $$\frac{28}{4a-a^{2}}-\frac{7}{a}$$ при $$a=-3$$
$$\frac{28}{4a-a^{2}}-\frac{7}{a}=\frac{28}{a(4-a)}-\frac{7(4-a)}{a(4-a)}=$$ $$\frac{28-2a+7a}{a(4-a)}=\frac{7}{4-a}=\frac{7}{4-(-3)}=1$$
Задание 13
Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле $$a=\omega^{2}R$$, где $$\omega$$— угловая скорость (в с-1), а $$R$$ — радиус окружности. Пользуясь этой формулой, найдите расстояние (в метрах), если угловая скорость равна 4 с-1, а центростремительное ускорение равно 96 м/с2.
$$R=\frac{a}{\omega^{2}}=\frac{96}{4^{2}}=6$$
Задание 14
Найдите сумму наибольшего целого и наименьшего целого решения системы $$\left\{\begin{matrix}x+4<2x+3\\3x-4\leq2x+4\end{matrix}\right.$$
$$\left\{\begin{matrix}x+4<2x+3\\3x-4\leq2x+4\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x-3<2x-x\\3x-2x\leq4+4\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x>1\\x\leq8\end{matrix}\right.$$
$$x_{min}=2$$; $$x_{max}=8$$
Задание 15
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина — 84 см.Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Диагональ ступеньки: $$\frac{\sqrt{13^{2}+84^{2}}}{100}=0,85$$
Количество ступенек: $$\frac{25,5}{0,85}=30$$
Высота: $$0,13\cdot30=3,9$$
Задание 16
В треугольнике АВС углы А и С равны 46° и 54° соответственно. Найдите угол между высотой ВН и биссектрисой BD. Ответ дайте в градусах.
$$\angle B=180^{\circ}-(46+54)=80$$; $$\angle DBC=\frac{\angle B}{2}=40$$; $$\bigtriangleup BHC$$: $$\angle HBC=90^{\circ}-\angle C=90-54=36^{\circ}$$; $$\angle DBH=40-36=4$$
Задание 17
Диагональ равнобедренной трапеции делит тупой угол пополам. Меньшее основание трапеции равно 5, а её периметр равен 24. Найдите большее основание трапеции.
$$\angle CBD=\angle ABD$$ (по условию)
$$\angle CBD=\angle ADB$$ (накрестлежащие)
тогда $$\bigtriangleup ABD$$ - равнобедр $$\Rightarrow$$ $$AB=CD=AD=x$$; $$P=3x+5=24$$; $$3x=19$$; $$x=\frac{19}{3}$$
Задание 20
Какие из следующих утверждений верны?
1. Если один из углов параллелограмма острый, то и остальные его углы острые.
2. Если один из углов параллелограмма прямой, то и остальные его углы прямые.
3. Если один из углов трапеции прямой, то и остальные её углы прямые
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Задание 21
Решите уравнение $$(x^{2}-25)^{2}+(x^{2}+3x-10)^{2}=0$$
$$\left\{\begin{matrix}x^{2}-25=0\\x^{2}+3x-10=0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\pm5\\\left\{\begin{matrix}x_{1}=-5\\x_{2}=2\end{matrix}\right.\end{matrix}\right.$$
Задание 22
Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростьюи15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.
Пусть х - скорость третьего. Время, за которое догонит второго: $$t_{2}=\frac{15\cdot1}{x-15}$$. Первого: $$t_{1}=\frac{21\cdot2}{x-21}$$
$$\frac{42}{x-21}-\frac{15}{x-15}=9$$; $$42x-42\cdot15-15x+21\cdot15=9(x^{2}-15x-21x+21\cdot15)$$; $$27x-315=9(x^{2}-36x+315)$$; $$3x-35=x^{2}-36x+315$$; $$x^{2}-39x+350=0$$
$$D=1521-1400=121$$; $$x_{1}=\frac{39+11}{2}=25$$; $$x_{2}=\frac{39-11}{2}=14$$ - не подходит.
Задание 23
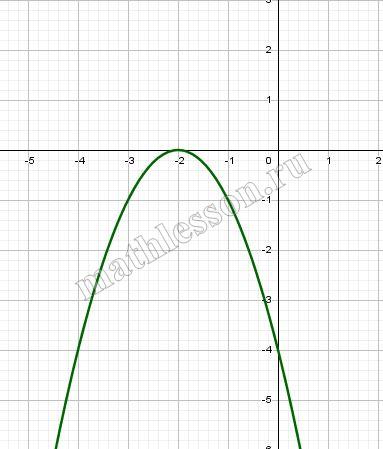
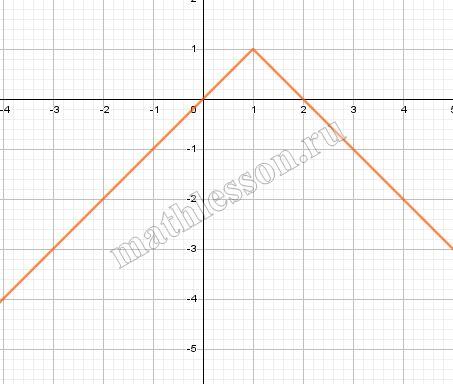
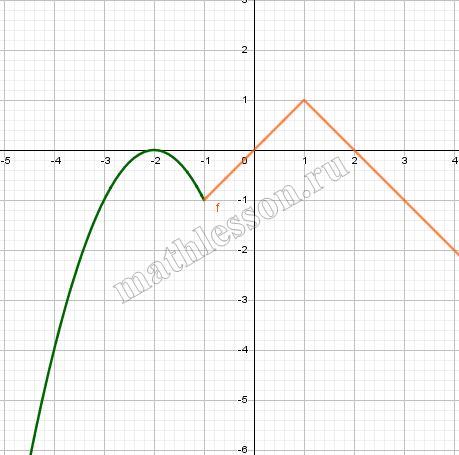
Постройте график функции
$$y=\left\{\begin{matrix}-x^{2}-4x-4,x<-1\\1-|x-1|,x\geq-1\end{matrix}\right.$$
и определите, при каких значениях $$m$$ прямая $$y=m$$ имеет с графиком ровно две общие точки.
Задание 24
Меньшее основание прямоугольной трапеции равно 12,5 см, а большая диагональ является биссектрисой угла при большем основании и равна 20 см. Найдите площадь трапеции.
1) $$\angle BDC=\angle ADB$$ (BD - биссект.); $$\angle CDB=\angle BDA$$ (накрестлежащие); $$\Rightarrow$$ $$\angle CBD=\angle BCD$$ $$\Rightarrow$$ $$BC=CD=12,5$$
2) $$CH$$ - высота, тогда $$AH=HD=12,5$$. Пусть $$AB=CH=x$$, $$HD=y$$,тогда: из $$\bigtriangleup CHD$$ и $$\bigtriangleup ABD$$: $$\left\{\begin{matrix}x^{2}+y^{2}=(12,5)^{2}\\x^{2}+(12,5+y)^{2}=20^{2}\end{matrix}\right.$$
$$20^{2}-(12,5+y)^{2}+y^{2}=12,5^{2}$$; $$400-12,5^{2}-25y-y^{2}+y^{2}-12,5^{2}=0$$; $$400-312,5=25y$$; $$y=3,5$$ $$\Rightarrow$$ $$x=\sqrt{400-256}=12$$
3) $$S=\frac{12,5+12,5+3,5}{2}\cdot12=171$$
Задание 25
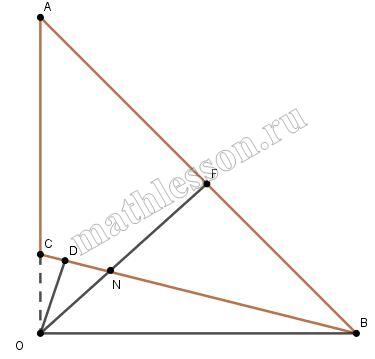
В треугольнике АВС угол АСВ тупой, $$BO\perp AC$$, $$OF\perp AB$$, $$OD\perp BC$$. Докажите, что $$\angle ACB=\angle DFB$$.
Пусть $$\angle A=\alpha$$; $$\angle B=\beta$$ $$\Rightarrow$$ $$\angle ACB=180-\angle\alpha-\angle\beta$$
1) $$\angle BCO=180-\angle C=\alpha+\beta$$ $$\Rightarrow$$ из $$\bigtriangleup OCB$$: $$\angle CBO=90^{\circ}-\angle BCO=90^{\circ}-\alpha-\beta$$
2) $$\bigtriangleup ODN\sim\bigtriangleup FNB$$ (прямоугольные); $$\angle DNO=\angle FNB$$ (как вертикал.); $$\Rightarrow$$ $$\frac{ON}{NB}=\frac{DN}{FN}$$ $$\Rightarrow$$ $$\frac{ON}{DN}=\frac{NB}{NF}$$ $$\Rightarrow$$ $$\angle DFN=\angle NBO=90^{\circ}-\alpha-\beta$$ $$\Rightarrow$$ $$\angle DFB=90^{\circ}+90^{\circ}-\alpha-\beta=180^{\circ}-\alpha-\beta=\angle ACB$$
ч.т.д.
Задание 26
В выпуклом четырёхугольнике ABCD точка Е – точка пересечения диагоналей. Известно, что площадь каждого из треугольников АВЕ и DСЕ равна 1, площадь четырёхугольника АВСD не превосходит 4, АD = 3. Найдите длину стороны ВС.
1) $$S_{ABC}=S_{CED}=1$$ $$\Rightarrow$$ $$BE\cdot AE=CE\cdot ED$$ $$\Rightarrow$$ $$\frac{BE}{ED}=\frac{CE}{EA}$$; $$\angle BEC=\angle AED$$ $$\Rightarrow$$ $$\bigtriangleup BEC\sim\bigtriangleup AED$$ $$\Rightarrow$$ дана трапеция.
2) Пусть НМ - высота $$\Rightarrow$$ $$S_{BEC}=\frac{1}{2}BC\cdot HE$$; $$S_{AED}=\frac{1}{2}EM\cdot AD$$. Пусть $$EM=x$$ $$\Rightarrow$$ $$HE=kx$$, где $$k$$ - коэфф. подобия $$\Rightarrow$$ $$BC=k\cdot3$$ $$\Rightarrow$$
$$S_{BEC}+S_{AED}=\frac{1}{2}\cdot3k\cdot kx+\frac{1}{2}\cdot3x=\frac{1}{2}\cdot3x(k^{2}+1)\leq2$$ $$\Rightarrow$$ $$x(k^{2}+1)\leq\frac{4}{3}$$ $$(1)$$
$$S_{ABCD}=\frac{3k+3}{2}\cdot(kx+x)<4$$ $$\Rightarrow$$ $$x(k+1)^{2}\leq\frac{8}{3}$$ $$(2)$$
Поделим первое на второе: $$\frac{k^{2}+1}{(k+1)^{2}}\leq\frac{4}{3}\cdot\frac{3}{8}$$ $$\Leftrightarrow$$ $$\frac{k^{2}+1}{(k+1)^{2}}\leq\frac{1}{2}$$ $$\Leftrightarrow$$ $$2k^{2}+2\leq k^{2}+2k+1$$ $$\Leftrightarrow$$ $$k^{2}-2k+1\leq0$$ $$\Leftrightarrow$$ $$(k-1)^{2}\leq0$$ $$\Leftrightarrow$$ $$k=1$$ $$\Rightarrow$$ $$BC=1\cdot3=3$$