ОГЭ математика 2022. Разбор варианта Алекса Ларина № 299.
Больше разборов на моем ютуб-канале
Задания 1-5
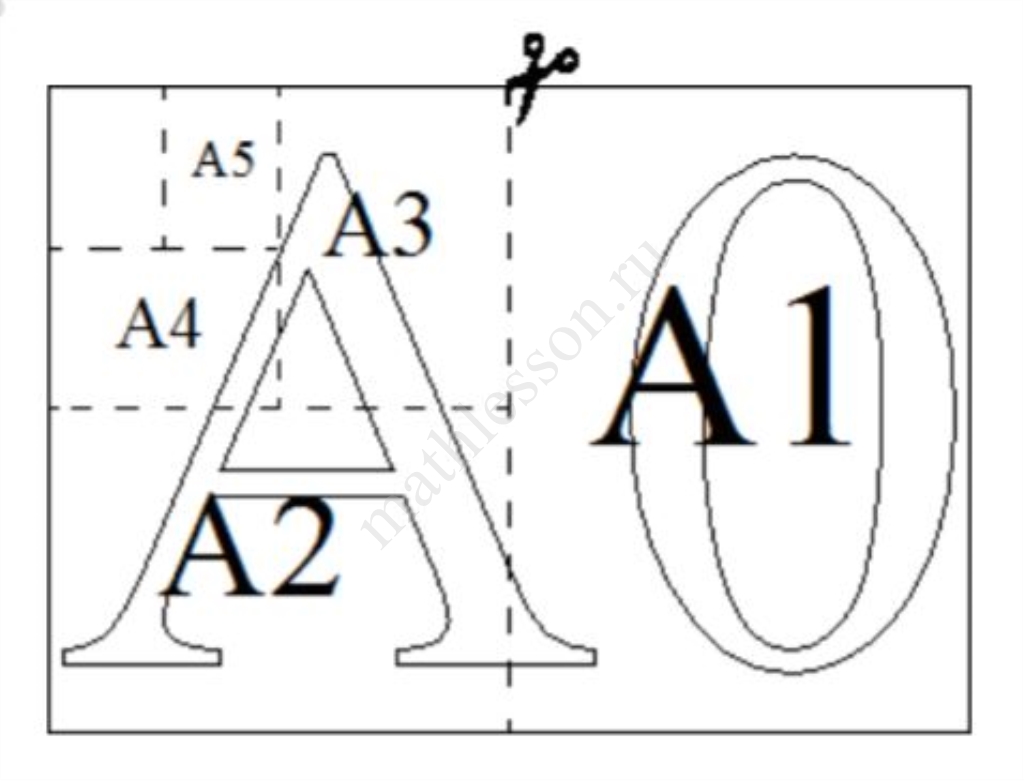
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2 (см. рис. выше). И так далее.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта, если изменяется формат листа.
В таблице (см. ниже) даны размеры (с точностью до мм) четырёх листов, имеющих форматы А3, А4, А5 и А6.
| Номер листа | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |
1. Установите соответствие между форматами и номерами листов. Заполните таблицу.
В ответе запишите последовательность четырёх чисел без пробелов и других разделительных символов.
| Формат | А3 | А4 | А5 | А6 |
| Номер |
2. Сколько листов бумаги формата А5 получится из одного листа бумаги формата А0?
3. Найдите длину (в мм) большей стороны листа бумаги формата А2. Результат округлите до десятков.
4. Найдите площадь (в см2) листа бумаги формата А3. Результат округлите до десятков.
5. Найдите отношение длины большей стороны к меньшей у бумаги формата А1. Ответ округлите до десятых.
Задание 11
Ниже представлены графики функций. Установите соответствие между графиками функций и формулами, которые их задают. В ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
- $$y=-\frac{1}{9x}$$
- $$y=-5x-4$$
- $$y=-\frac{x}{4}+5$$
- $$y=2x^{2}-8x+4$$
Задание 12
Площадь четырёхугольника можно вычислить по формуле $$S=\frac{1}{2}d_{1}d_{2}\sin \phi$$, где d1 и d2 — длины диагоналей четырёхугольника, $$\phi$$ — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали $$d_{2}$$, если $$d_{1}=6, \sin \phi=\frac{1}{12}$$, a S=3,75.
Задание 19
Какие из следующих утверждений верны? Если верных утверждений несколько запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Треугольника со сторонами 1, 2, 4 не существует.
- Смежные углы равны.
- Все диаметры окружности равны между собой.
Задание 21
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина товарного поезда равна 900 метрам. Найдите длину (в метрах) пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.