ОГЭ математика 2019. Разбор варианта Алекса Ларина № 187.
Решаем ОГЭ 187 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №187 (alexlarin.com)
Решаем ОГЭ 187 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №187 (alexlarin.com)
Задание 1
Найдите значение выражения: $$\frac{8,4-\frac{2}{3}}{\frac{5}{12}-0,25}$$
$$\frac{8,4-\frac{2}{3}}{\frac{5}{12}-0,25}=$$$$\frac{\frac{84}{10}-\frac{2}{3}}{\frac{5}{12}-\frac{0,25}{100}}=$$$$\frac{\frac{42}{5}-\frac{2}{3}}{\frac{5}{12}-\frac{1}{4}}=$$$$\frac{\frac{126-10}{5*3}}{\frac{5-3}{12}}=\frac{232}{5}=46,4.$$
Задание 2
| Команда | 1 эстафета, мин. | 2 эстафета, мин. | 3 эстафета, мин | 4 эстафета, мин |
| Мотор | 3,4 | 4,9 | 2,9 | 5,8 |
| Тайфун | 4,5 | 4,3 | 3,2 | 5,4 |
| Пламя | 4,9 | 4,8 | 2,7 | 6,3 |
| Парус | 3,7 | 4,5 | 2,4 | 5,1 |
| Команда | 1 эстафета, место | 2 эстафета, место | 3 эстафета, место | 4 эстафета, место | итоговый бал |
| Мотор | 1 | 4 | 3 | 3 | 11 |
| Тайфун | 3 | 1 | 4 | 2 | 10 |
| Пламя | 4 | 3 | 2 | 4 | 13 |
| Парус | 2 | 2 | 1 | 1 | 6 |
В итоге команда Пламя займет 4 место, что соответствует 4 варианту ответа
Задание 3
Между какими числами заключено число $$5\sqrt{3}$$?
Варианты ответа:
- 5 и 6
- 6 и 7
- 7 и 8
- 8 и 9
$$5\sqrt{3}=\sqrt{5^{2}*3}=\sqrt{75}$$. Число $$\sqrt{75}$$ расположено между $$\sqrt{64}=8$$ и $$\sqrt{81}=9$$. Т.е. ответ 4 вариант
Задание 4
Представьте выражение $$\frac{(c^{-3})^{5}}{c^{-6}}$$ в виде степени с основанием c.
Варианты ответа
- $$c^{9}$$
- $$c^{-9}$$
- $$c^{2}$$
- $$c^{-14}$$
$$\frac{(c^{-3})^{5}}{c^{-6}}=\frac{c^{-3*5}}{c^{-6}}=$$$$\frac{c^{-15}}{c^{-6}}=$$$$c^{15-(-6))}=c^{-9}$$. Что соответствует 2 варианту ответа
Задание 5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры. Ответ дайте в градусах Цельсия.
$$t_{max}=24$$( между 12 и 15:00); $$t_{min}=8$$( между 21:00 и 00:00); $$t_{max}-t_{min}=24-8=16;$$
Задание 6
Решите уравнение: $$\frac{x+5}{6}-\frac{x}{5}=1$$
$$\frac{x+5}{6}-\frac{x}{5}=1$$ $$\frac{5(x+5)-6x}{6*5}=\frac{6*5}{6*5}$$ $$5x+25-6x=30$$ $$-x=30-25=5$$ $$x=-5.$$
Задание 7
На первую смену в лагерь было выделено 72 льготные путёвки. На вторую смену – на 25% больше. Сколько льготных путёвок было выделено во вторую смену?
Пусть x- число путевок во 2 смену. Если 72-100%, то x-(100+25)% 72-100% x-125% $$x=\frac{72*125}{100}=90$$ путевок.
Задание 8
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.
Какие из следующих утверждений неверны?
- пользователей из России больше, чем пользователей из Украины;
- больше трети пользователей сети — из Украины;
- пользователей из Беларуси больше, чем пользователей из Украины;
- пользователей из России больше 4 миллионов человек.
- верно;
- неверно-сегмент Украины меньше $$\frac{1}{3}$$ круга;
- неверно- сегмент Белоруси меньше чем Украины;
- верно
Задание 9
В соревнованиях по метанию копья участвуют 11 спортсменов из России, 6 спортсменов из Испании и 3 спортсмена из Канады. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что первым будет выступать спортсмен из России.
Общее количество спортсменов $$N=11+6+3=20$$ Вероятность первого из РФ: $$P=\frac{n}{N}=\frac{11}{20}=0,55$$.
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
- $$y=2x$$
- $$y=x^{2}-2$$
- $$y=\sqrt{x}$$
- $$y=-\frac{2}{x}$$
| А | Б | В |
| 2 | 1 | 4 |
$$y=2x$$-линейная функция $$\Rightarrow$$ Б; $$y=x^{2}-2$$ – квадратичная функция $$\Rightarrow$$ А; $$y=\sqrt{x}$$ - график-ветвь параболы ,его нет на рисунке; $$y=-\frac{2}{x}$$ - гипербола $$\Rightarrow$$ В
Задание 11
В первом ряду кинозала 18 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в десятом ряду?
Воспользуемся формулами арифметической прогрессии: $$a_{1}=18 ; d=2; n=10;$$ $$a_{n}=a_{1}+d*(n-1);$$, тогда $$a_{10}=18+2*(10-1)=36.$$
Задание 12
Найдите значение выражения $$\frac{ab +b^{2}}{54a }*\frac{9a}{a +b}$$, при $$a=0,5 ; b=-6,9$$
$$\frac{ab +b^{2}}{54a }*\frac{9a}{a +b}=$$$$\frac{b(a +b)}{54a}*\frac{9a}{a +b}=$$$$\frac{b}{6}=\frac{-6,9}{6}=-1,15$$
Задание 13
Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула $$F=1,8C+32$$ , где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 194 по шкале Фаренгейта? Ответ округлите до десятых.
Выразим градусы Цельсия из формулы: $$1,8C=F-32\Leftrightarrow$$$$C=\frac{F-32}{1,8}$$ Тогда $$C=\frac{194-32}{1,8}=\frac{162}{1,8}=90.$$
Задание 14
На каком рисунке изображено множество решений неравенства $$x^{2}-2x-3 \geq 0$$. Укажите неравенство, которое не имеет решений.
Решим уравнение $$x^{2}-2x-3=0$$
$$\left\{\begin{matrix}x_{1} +x_{2}=2& & \\x_{1}*x_{2}=-3 & &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x_{1}=3 & & \\x_{2}=-1 & &\end{matrix}\right.$$
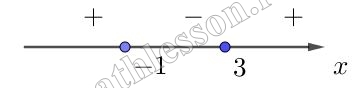
Отметим полученные точки на координатной прямой и расставим знаки выражения
Нам нужны неотрицательные значения $$\Rightarrow x\in (-\infty ;-1] \cup [3 ;+\infty ]$$, соответствует 2 варианту ответа.
Задание 15
Пол комнаты, имеющий форму прямоугольника со сторонами 7 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 40 см. Сколько потребуется таких дощечек?
Найдем площадь пола : $$S_{1}=7,8=5*6$$ квадратных метров Найдем площадь дощечки : $$S_{2}=0,1*0,4=0,04$$ квадратных метров Количество дощечек: $$n=\frac{S_{1}}{S_{2}}=\frac{56}{0,04}=1400$$.
Задание 16
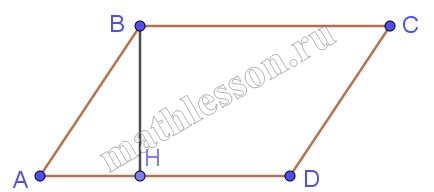
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 38° и 55°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Один угол: 38+55=93. Тогда второй по свойству углов параллелограмма: 180-93=87.
Задание 18
Найдите площадь квадрата, если его диагональ равна 6.
Пусть $$a$$–сторона квадрата, тогда его площадь: $$S=a^{2}$$. По т. Пифагора $$\sqrt{a^{2}+a^{2}}\Rightarrow$$$$ 2a ^{2}=36\Leftrightarrow a ^{2}=18=S$$.
Задание 19
Построим центральный угол AOC. $$\angle AOC=135\Rightarrow$$$$ \angle ABC=\frac{\angle AOC}{2}=67,5$$.
Задание 20
Какие из следующих утверждений верны?
- Смежные углы равны.
- Вертикальные углы равны
- Накрест лежащие углы равны.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
- неверно. Они дают в сумме 180;
- верно;
- неверно, только при параллельных прямых
Задание 21
Решите систему уравнений: $$\left\{\begin{matrix}5(2x-1)+1=6(y+1)-8 & & \\2(x+3y)+5=3(y-2x)+4 & &\end{matrix}\right.$$
$$\left\{\begin{matrix}5(2x-1)+1=6(y+1)-8\\2(x+3y)+5=3(y-2x)+4\end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}10x-5+1-6y-6+8=0\\2x+6y+5-3y+6x-4=0\end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}10x-6y-2=0\\8x+3y+1=0 \end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}10x-6y-2=0\\16x+6y+2=0\end{matrix}\right.$$ Сложим первое и второе , $$10x+16x-6y+6y-2+2=0$$ $$26x=0 \Rightarrow x=0$$ Тогда : $$10*0-6y-2=0 \Leftrightarrow 6y=-2 \Leftrightarrow y=-\frac{1}{3}$$
Задание 22
При одновременной работе двух труб бассейн наполняется за 7 ч 18 мин. За какое время наполняется бассейн каждой трубой в отдельности, если через одну трубу он наполняется на 6 ч быстрее, чем через другую?
Пусть 1- объем бассейна , х- производительность 1-ой трубы в частях бассейна в час, y-2-ой . Тогда :
$$\left\{\begin{matrix}\frac{1}{x+y}=7\frac{12}{60} \\\frac{1}{x}-\frac{1}{y}=6\end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}\frac{1}{x+y}=\frac{72}{10}(1)\\\frac{1}{x}-\frac{1}{y}=6(2)\end{matrix}\right.$$
1)$$72x+72y=10\Leftrightarrow x=\frac{10-72y}{72}$$
Подставим во второе $$\frac{72}{10-72y}-\frac{1}{y}=6\Leftrightarrow 72y-10+72y=60y-432y^{2}$$ $$432y^{2}+84y-10\Leftrightarrow 216y^{2}+42y-5=0$$
$$D=1764+4320=6084=78^{2}$$
$$y_{2}=\frac{-42+78}{2*216}=\frac{36}{2*216}=\frac{1}{12} y_{2}< 0$$
$$x_{1}=\frac{10-72*\frac{1}{12}}{72}=\frac{4}{72}=18.$$
Задание 23
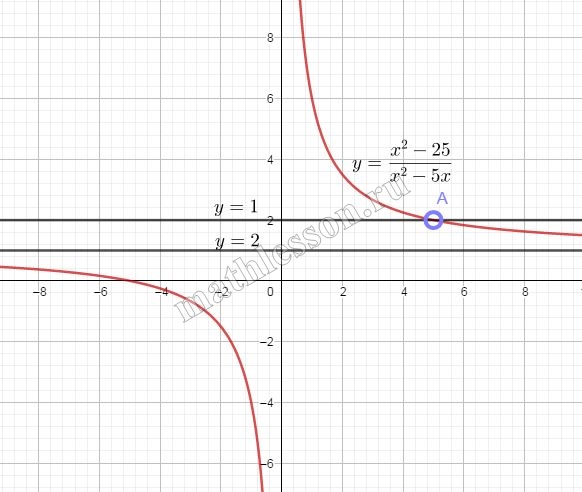
Постройте график функции $$y=\frac{x^{2}-25}{x^{2}-5x}$$ и определите, при каких значениях a прямая $$y=a$$ не имеет с графиком ни одной общей точки.
$$y=\frac{x^{2}-25}{x^{2}-5x}$$
ОДЗ: $$x^{2}-5x\neq 0 \Leftrightarrow x(x-5)=0\Leftrightarrow$$$$ x\neq 0; x\neq 5\Rightarrow x\in (-\infty; 0)\cup(5 ;+\infty ).$$
Упростим выражение: $$\frac{x^{2}-25}{x^{2}-5x}=\frac{(x-5)*(x+5)}{x(x-5)}=\frac{x+5}{x}=1+\frac{5}{x}$$ Т.е. график $$y=1+\frac{5}{x}$$ такой же, как $$y=\frac{x^{2}-25}{x^{2}-5x}$$ при условии ОДЗ:
Прямая $$y=a$$ - это прямая, параллельная оси Ох. Она не будет иметь пересечения с графиком исходной функции при a=2 и a=1.
Задание 24
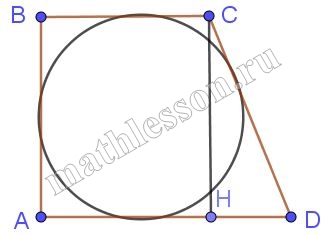
В прямоугольную трапецию с основаниями 5 см и 6 см вписана окружность. Найдите площадь этой трапеции.
1) BC=5; CD=6; опустим $$CH\perp AD$$ , тогда $$HD=6-5=1$$.
2) Пусть AB=x, тогда CH=x Пусть CD=y , тогда из $$\Delta CHD: x^{2}+1^{2}=y^{2}$$
По свойству описанного многоугольника : $$5+6=x+y$$. Тогда:
$$\left\{\begin{matrix}x^{2} +1=y^{2}\\x+y-11 & &\end{matrix}\right.\Leftrightarrow$$$$ \left\{\begin{matrix}x^{2}+1=(11-x)^{2} \\y=11-x\end{matrix}\right.$$
3)$$S=\frac{5+6}{2}*\frac{60}{11}=30$$.
Задание 25
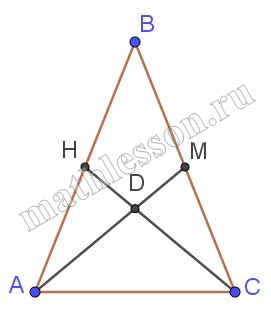
Докажите, что если у треугольника равны две медианы, то этот треугольник равнобедренный.
1) Пусть АМ=СН-медианы . $$\frac{LN}{LM}=\frac{2}{1}$$ и $$\frac{CL}{CH}=\frac{2}{1}$$(свойство медиан), но т.к. AM=CH, то AL=LC ,LH=LM.
2) $$\angle HLA=\angle MLC$$ (вертикальные) $$\Delta HLA=\Delta MLC$$ (по 2-м сторонам и углу между ними) $$\Rightarrow$$ AH=MC, но AH=HB и CM=MB $$\Rightarrow$$ AB=BC.
Задание 26
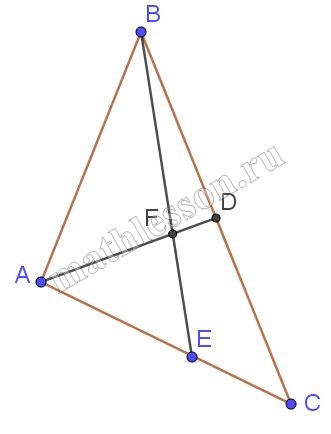
В треугольнике АВС биссектриса АD делит сторону ВС на отрезки ВD и DС, причем ВD : DС = 3:2. На стороне АС выбрана точка Е такая, что биссектриса АD пересекает ВЕ в точке F и ВF : FЕ = 5 : 2. Найдите площадь четырехугольника FDCE, если площадь треугольника АВС равна 70 см2 .
1) По т. Менелая из $$\Delta ADC:$$
$$\frac{BF}{FE}*\frac{EA}{AC}*\frac{CD}{BD}=1\Rightarrow$$ $$\frac{EA}{AC}=\frac{2}{5}*\frac{3}{2}=\frac{3}{5}\Rightarrow \frac{AE}{EC}=\frac{3}{2}$$;
2) по т. Менелая $$\Delta BEC$$:
$$\frac{AF}{FD}*\frac{DB}{BC}*\frac{CE}{EA}=1\Rightarrow \frac{AF}{FD}=\frac{5}{3}*\frac{3}{2}=\frac{5}{2}$$
3) $$S_{ADC}= \frac{DC}{BC}; S_{ABC}=\frac{2}{5}*70=28$$
4) $$\frac{S_{AFE}}{S_{ADC}}=\frac{AF*AE}{AD*AC}=\frac{\frac{5}{7}AD*\frac{3}{5}AC}{AD*AC}=\frac{3}{7}$$, тогда $$S_{FDCE}=\frac{4}{7}*S_{ADC}=\frac{4}{7}*28=16$$