ОГЭ математика 2019. Разбор варианта Алекса Ларина № 202.
Решаем ОГЭ 202 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина № 202 (alexlarin.com)
Решаем ОГЭ 202 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина № 202 (alexlarin.com)
Задание 1
Найдите значение выражения: $$(8\frac{11}{12}-9\frac{7}{12}):\frac{2}{9}$$
$$(8\frac{11}{12}-9\frac{7}{12}):\frac{2}{9}=$$$$(-1+\frac{4}{12})*\frac{9}{2}=$$$$\frac{8}{12}*\frac{9}{2}=3$$
Задание 2
В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40–97 | 70–154 | 60–102 |
| Белки | 36–87 | 65–117 | 58–87 |
| Углеводы | 170–420 | 257–586 | |
Какой вывод о суточном потреблении жиров, белков и углеводов мужчиной можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 150 г жиров, 120 г белков и 611 г углеводов? В ответе укажите номера верных утверждений.
- Потребление жиров в норме - верно, $$150 \in [70;154]$$
- Потребление белков в норме - неверно, $$120 \in [65;117]$$
- Потребление углеводов в норме - неверно, $$611\in [257;586]$$
Верен только первый вариант ответа
Задание 3
Значение какого из данных выражений положительно, если известно, что a>0, b<0?
Варианты ответа
Пусть a=2, b=-3, тогда
- $$ab=2(-3)=-6<0$$
- $$(2-(-3))*(-3)=-15<0$$
- $$(-3-2)(-3)=15>0$$
- $$(-3-2)*2=-10<0$$
Положителен 3 вариант ответа
Задание 4
Значение какого из данных выражений является рациональным числом?
Варианты ответа
- $$\frac{(\sqrt{5})^{3}}{5}$$
- $$2\sqrt{2^{5}}$$
- $$\frac{\sqrt{5}}{\sqrt{45}}$$
- $$\sqrt{2}\cdot \sqrt{12}$$
- $$\frac{(\sqrt{5})^{3}}{5}=$$$$\frac{5\sqrt{5}}{5}=\sqrt{5}$$ - иррациональное
- $$2\sqrt{2^{5}}=$$$$8\sqrt{2}$$ - иррациональное
- $$\frac{\sqrt{5}}{\sqrt{45}}=$$$$\frac{1}{\sqrt{9}}=\frac{1}{3}$$ - рациональное
- $$\sqrt{2}*\sqrt{12}=$$$$\sqrt{24}=2\sqrt{6}$$ - иррациональное
Задание 5
На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за последние два часа программы по сравнению с первыми двумя часами этой программы.
За последние два часа прислано: 70+80=150 сообщений, за первые два: 70+40=110 сообщений. Разница составляет 150-110=40 сообщений
Задание 6
Решите уравнение $$3(-5-3x)-6=2(x+3)-x$$
$$3(-5-3x)-6=2(x+3)-x\Leftrightarrow$$$$-15-9x-6=2x+6-x\Leftrightarrow$$$$-9x+x-2x=6+6+15\Leftrightarrow$$$$-10x=27\Leftrightarrow x=-2,7$$
Задание 7
Число отдыхающих в санатории зимой уменьшилось в 5 раз по сравнению с летом. На сколько процентов уменьшилось число отдыхающих зимой?
Пусть было 100% , уменьшим в 5 раз $$\Rightarrow$$ стало 20% , следовательно, уменьшилось на 100-20=80%
Задание 8
На диаграмме показано распределение земель Южного федерального округа по категориям.
*прочие земли — это земли поселений; земли промышленности и иного специального назначения; земли особо охраняемых территорий и объектов. Сколько примерно квадратных километров занимают земли запаса, если площадь Южного округа составляет 416 840 км2?
Варианты ответа:
Земли запаса составила примерно $$\frac{1}{20}$$ от площади ЮФО $$\Rightarrow$$ $$\frac{416840}{20}\approx$$ 20 тысяч, что соответствует 1 варианту ответа.
Задание 9
Анна выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 99.
Всего трехзначных чисел 999-99=900. Из них делится на 99 одно на каждые 100$$\Rightarrow$$ 9 чисел, тогда вероятность $$P=\frac{9}{900}=0,01$$.
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
ФОРМУЛЫ
- A - ветви параболы $$\Rightarrow$$ $$y=\sqrt{3}(3)$$
- Б - параболы $$\Rightarrow$$ $$y=x^{2}-4(1)$$
- B - прямая $$\Rightarrow$$ $$y=2x-4(2)$$
Задание 11
Последовательность (bn) задана условиями $$b_{1}=-5, b_{n+1}=-2*\frac{1}{b_{n}}$$. Найдите $$b_{4}$$
- $$b_{2}=-2*\frac{1}{b_{1}}=$$$$-2*\frac{1}{-5}=\frac{2}{5}$$
- $$b_{3}=-2*\frac{1}{b_{2}}=$$$$-2*\frac{1}{\frac{2}{5}}=-5$$
- $$b_{4}=-2*\frac{1}{b_{3}}=$$$$-2*\frac{1}{-5}= \frac{2}{5}=0,4$$
Задание 12
Квадратный трехчлен разложен на множители $$4x^{2}-5x-6=4(x-2)(x-a)$$. Найдите а
$$4x^{2}-5x-6=4(x-2)(x-a)$$
Пусть : $$4x^{2}-5x-6=0$$
$$D=25+96=121$$
$$x_{1}=\frac{5+11}{8}=2$$
$$x_{2}=\frac{5-11}{8}=-0,75$$
Тогда: $$4x^{2}-5x-6=4(x-2)(x-(-0,75))\Rightarrow$$ $$a=-0,75$$
Задание 13
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле C=150+11(t−5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 16-минутной поездки. Ответ укажите в рублях.
Найдем с: $$c=150+11(16-5)=150+11*11=271$$
Задание 14
На каком рисунке изображено множество решений системы неравенств $$\left\{\begin{matrix}2x-3<1\\ 5-3x>8\end{matrix}\right.$$
$$\left\{\begin{matrix}2x-3<1\\5-3x>8\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2x<4\\-3x>3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x<2\\x<-1\end{matrix}\right.\Leftrightarrow$$ $$x<-1$$, что соответствует 3 варианту ответа ( т.к. $$(-4;1) \in (-\infty ;-1)$$ )
Задание 15
Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?
Площадь комнаты: $$S=4*10=40$$ м2
Площадь дощечки: $$\frac{5}{100}*\frac{20}{100}=0,01$$ м2
Количество дощечек: $$n=\frac{40}{0,01}=4000$$
Задание 16
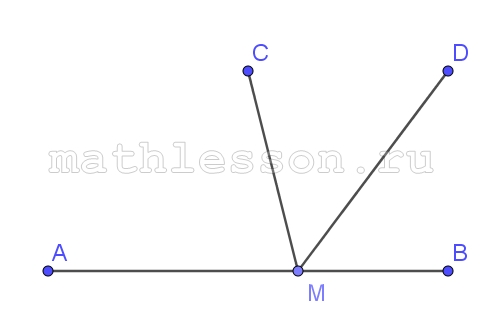
На прямой АВ взята точка М. Луч MD — биссектриса угла CMВ. Известно, что $$\angle DMC=48$$. Найдите угол CMA. Ответ дайте в градусах
$$\angle BMC=2*48=96$$ (MD - биссектрисса)
$$\angle AMC=180-\angle BMC=84$$ (свойство смежных)
Задание 17
Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.
По т. Пифагора : $$\sqrt{7^{2}+24^{2}}=25$$
Задание 18
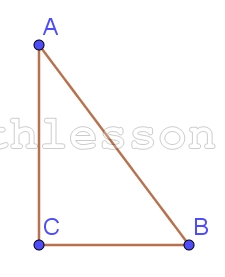
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC
$$\frac{DE}{AB}=\frac{1}{2}=k\Rightarrow$$ $$\frac{S_{DCE}}{S_{ABC}}=k^{2}=\frac{1}{4}\Rightarrow$$ $$S_{ABC}=8*4=32$$
Задание 19
Катеты прямоугольного треугольника равны $$5\sqrt{3}$$ и 5. Найдите синус наименьшего угла этого треугольника.
Пусть CB=5; $$AC=5\sqrt{3}$$; $$CB<AC$$ $$\Rightarrow$$ $$\angle A<\angle B$$ и $$\sin A$$ - наименьший
$$AB=\sqrt{AC^{2}+CB^{2}}=10$$; $$\sin A=\frac{CB}{AB}=0,5$$
Задание 20
Какие из следующих утверждений верны?
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
1) верно 2) неверно(как угодно могут - в зависимости от отношения длин оснований) 3) неверно (не хватает угла между сторонами)
Задание 21
Решите уравнение $$x^{2}+\frac{25x^{2}}{(x+5)^{2}}=\frac{125}{4}$$
$$x^{2}+\frac{25x^{2}}{(x+5)^{2}}=\frac{125}{4}$$
ОДЗ: $$x+5\neq 0\Rightarrow$$ $$x\neq -5$$
$$x^{2}+(\frac{5x}{x+5})^{2}+2*\frac{x*5x}{x+5}-2*\frac{x*5x}{x+5}=\frac{125}{4}\Leftrightarrow$$$$(x-\frac{5x}{x+5})^{2}+\frac{10x^{2}}{x+5}=\frac{125}{4}\Leftrightarrow$$$$(\frac{x^{2}+5x-5x}{(x+5)})^{2}+10*\frac{x^{2}}{x+5}-\frac{125}{4}=0\Leftrightarrow$$$$(\frac{x^{2}}{x+5})^{2}+10*\frac{x^{2}}{x+5}-\frac{125}{4}=0$$
Пусть $$\frac{x^{2}}{x+5}=y$$: $$y^{2}+10y-\frac{125}{4}=0$$
$$\left[\begin{matrix}\frac{x^{2}}{x+5}=\frac{5}{2}\\\frac{x^{2}}{x+5}=-\frac{25}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}2x^{2}-5x-25=0(1)\\2x^{2}+25x+125=0(2)\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=5\\x=-2,5\end{matrix}\right.$$
1) D=25+200=225: $$\left[\begin{matrix}x_{1}=\frac{5+15}{4}=5\\x_{2}=\frac{5-15}{4}=-\frac{5}{2}\end{matrix}\right.$$
2) D=625-1000<0 - решений нет
Задание 22
Из пункта А круговой трассы выехал велосипедист. Через 20 минут он ещё не вернулся в пункт А, откуда следом за ним отправился мотоциклист. Через 15 минут после отправления он догнал велосипедиста в первый раз, а ещё через 40 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 40 км.
Пусть x-км\ч - скорость велосипедиста, y км\ч - мотоциклиста. Тогда: $$\frac{35}{60}x=\frac{15}{60}y$$ (догнал через 15 минут, выехал на 20 минут позже) и $$\frac{40}{60}y-\frac{40}{60}x=40$$ (через 40 минут опережал на круг)
$$\left\{\begin{matrix}\frac{7}{12}x=\frac{1}{4}y\\\frac{y}{60}-\frac{x}{60}=1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}7x=3y\\y-x=60\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y=60+x\\7x=180+3x\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y=105\\x=45\end{matrix}\right.$$
Задание 23
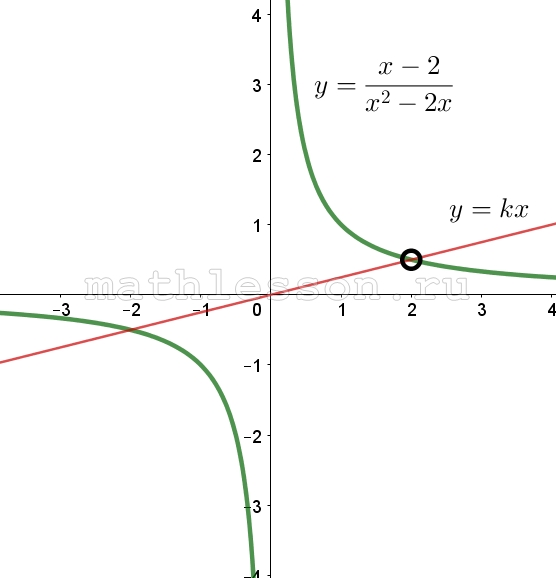
Постройте график функции $$y=\frac{x-2}{x^{2}-2x}$$ и определите, при каких значениях k прямая $$y=kx$$ имеет с графиком ровно одну общую точку.
Найдем ограничения по x: $$x^{2}-2x\neq 0\Leftrightarrow$$ $$x\neq 0 x\neq 2(1)$$. Тогда $$y=\frac{x-2}{x(x-2)}=\frac{1}{x}$$ с учетом (1) аналогичен искомой функции
Построим график функции:
$$y=kx$$ имеет 1 общую точку если проходит через (2;0,5): $$0,5=2k\Rightarrow$$ $$k=\frac{1}{4}$$
Задание 24
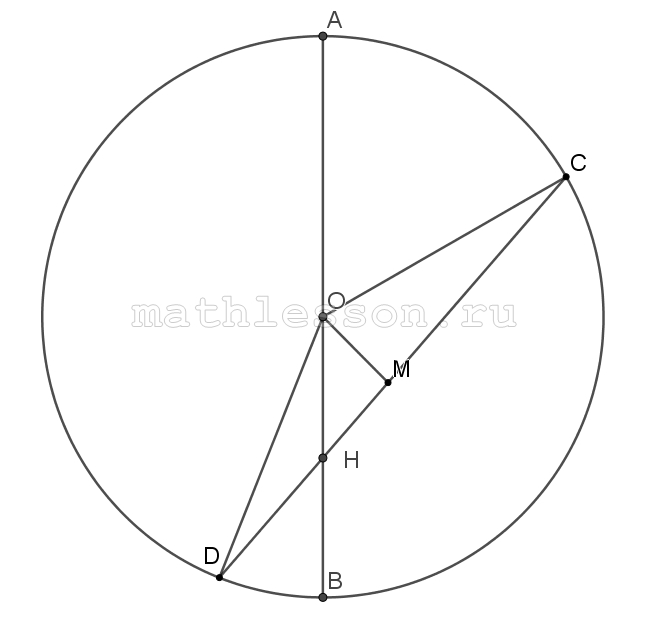
Хорда круга пересекает диаметр под углом 30 и делит его на части длиной 11 см и 55 см. Найдите расстояние от центра круга до хорды.
1) $$AB=AH+HB=66$$$$\Rightarrow$$ $$OA=OB=33$$(радиусы)
2) $$OH=OB-HB=33-11=22$$
3) из $$\Delta OHM$$: $$OM=OH*\sin OHM$$; $$OM=22*\frac{1}{2}=11$$
Задание 25
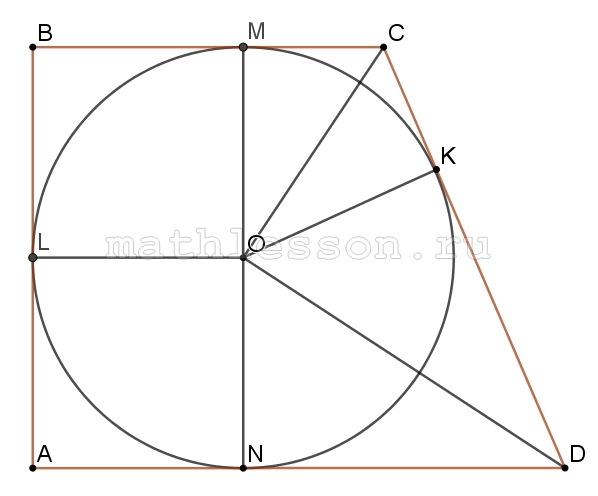
Докажите, что площадь прямоугольной трапеции, в которую можно вписать окружность, равна произведению длин её оснований.
1) т.к. можно вписать окружность , то $$AB+CD=BC+AD$$
2) $$S_{ABCD}=\frac{BC+AD}{2}*MN$$
Пусть $$OK\perp CD$$(OK-радиусы) . По свойству касательных : $$MC=CK$$, $$OM\perp CD\Rightarrow$$ $$\Delta MCO=\Delta CKO$$(по катету и гипотенузе) , аналогично, $$\Delta OKD=\Delta ODN$$. Тогда: $$\angle KDO=\angle ODN=\frac{\angle D}{2}=\frac{\alpha }{2}$$ и $$\angle MCO=\angle OCK=\frac{\angle C}{2}=\frac{180-\alpha }{2}=90-\frac{\alpha }{2}$$
Тогда: $$\angle COD=180-\frac{\alpha }{2}-(90-\frac{\alpha }{2})=90\Rightarrow$$ $$OK=\sqrt{CK*KD}$$.
Пусть CK=a, KD=b, OK=r, тогда: OL=OM=r; BM=BL; $$\angle B=90\Rightarrow$$ $$BM=BL=r$$; $$r^{2}=ab$$, $$BC=BM+MC=r+a$$, $$AD=AN+ND=r+b$$, $$AB=2r$$
3) $$S=\frac{r+a+r+b}{2}*2r=$$$$(2r+a+b)*2=2r^{2}+ar+br=$$$$r^{2}+r^{2}+ar+br=$$$$r^{2}+ab+ar+br=$$$$r(r+b)+a(r+b)=(r+b)(r+a)=AD*BC$$
Задание 26
Вершина С прямоугольника ABCD лежит на стороне КМ равнобедренной трапеции АВКМ (ВК || АМ), Р – точка пересечения отрезков АМ и СD. Найдите отношение площадей прямоугольника и трапеции, если АВ = 2ВС, АР = 3ВК.
1) Построим через $$CH\left | \right |AM$$ ($$H=CH\cap AB$$)
Пусть $$HK\cap BC=N$$; HBKC - равнобедренная трапеция $$\Rightarrow$$ BC=HK
Пусть $$BC=x=HK$$; $$AB=2x\Rightarrow$$ $$S_{ABCD}=BC*AB=2x^{2}$$
2) $$\Delta BKN\sim \Delta HNC$$; $$\frac{BN}{NC}=\frac{BK}{HC}(1)$$; $$HC\left | \right |AM$$ и $$AB\left | \right |CD\Rightarrow$$ HCPA - параллелограмм и HC=AP
С учетом (1): $$\frac{BN}{NC}=\frac{BK}{HC}=\frac{BK}{AP}=\frac{1}{3}\Rightarrow$$ $$BN=\frac{1}{4}*BC=\frac{x}{4}$$, $$NC=\frac{3}{4}*BC=\frac{3x}{4}=NH$$
3) из $$\Delta BNH$$: $$BH=\sqrt{NH^{2}-BN^{2}}=\frac{x}{\sqrt{2}}$$
$$tg\angle BHC=\frac{BC}{BH}=\frac{x}{\frac{x}{\sqrt{2}}}=$$$$\sqrt{2}=tg\angle A\Rightarrow$$ $$\sin A=\sqrt{\frac{2}{3}}$$, $$\cos A=\sqrt{\frac{1}{3}}$$
$$HC=\frac{BC}{\sin HBC}=\frac{x\sqrt{3}}{\sqrt{2}}\Rightarrow$$ $$BK=\frac{x\sqrt{3}}{3\sqrt{2}}$$
4)Пусть $$BL\perp AM$$, тогда из $$\Delta ABL$$: $$AL=AB*\cos A=2x*\frac{\sqrt{1}}{\sqrt{3}}=\frac{2x}{\sqrt{3}}\Rightarrow$$ $$AM=BK+2AL=\frac{x\sqrt{3}}{3\sqrt{2}}+\frac{2*2x}{\sqrt{3}}=$$$$\frac{x(\sqrt{3}+4\sqrt{6})}{3\sqrt{2}}$$, $$BL=AB \sin A=\frac{2x\sqrt{2}}{\sqrt{3}}$$
$$S_{ABKM}=\frac{\frac{x\sqrt{3}}{3\sqrt{2}}+\frac{x\sqrt{3}+x*4\sqrt{6}}{3\sqrt{2}}}{2}*\frac{2x\sqrt{2}}{\sqrt{3}}=$$$$\frac{2x\sqrt{3}+4x\sqrt{6}}{6\sqrt{2}}*\frac{2x\sqrt{2}}{\sqrt{3}}=$$$$\frac{2x^{2}(\sqrt{3}+2\sqrt{6})}{3\sqrt{3}}$$
5) $$\frac{S_{ABCD}}{S_{ABKM}}=2x^{2}:\frac{2x^{2}(\sqrt{3}+2\sqrt{6})}{3\sqrt{3}}=$$$$\frac{3\sqrt{3}}{\sqrt{3}+2\sqrt{6}}=$$$$\frac{3\sqrt{3}}{\sqrt{3}(1+2\sqrt{2})}=\frac{3}{1+2\sqrt{2}}$$