ОГЭ математика 2019. Разбор варианта Алекса Ларина № 201.
Решаем ОГЭ 201 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина № 201 (alexlarin.com)
Решаем ОГЭ 201 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина № 201 (alexlarin.com)
Задание 1
Найдите область определения выражения $$\sqrt{x-\frac{8}{x-2}}$$
$$\sqrt{x-\frac{8}{x-2}}\Leftrightarrow$$ $$\left\{\begin{matrix}x-2\neq 0\\x-\frac{8}{x-2}\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq 2\\\frac{x^{2}-2x-8}{x-2}\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq 2\\\frac{(x-4)(x+2)}{x-2}\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x\geq 4\\\left\{\begin{matrix}x\leq 2\\x>-2\end{matrix}\right.\end{matrix}\right.$$
Задание 2
Один сплав содержит 20%, а другой – 30% олова. Сколько килограммов первого и второго сплавов нужно взять, чтобы получить 10 кг 27%-го сплава олова?
Пусть x(кг ) – масса первого сплава, тогда 0,2x - масса олова в нем , 10-x - второго сплава, 0,3(10-x) – олова в нем. Тогда:
$$0,2x+0,3(10-x)=0,27*10\Leftrightarrow$$$$0,2x+3-0,3x=2,7\Leftrightarrow$$$$-0,1x=-0,3\Rightarrow$$$$x=3$$(кг) первый, тогда 10-3=7 кг – второй
Задание 3
Постройте график функции $$y=\frac{2|x|-1}{|x|-2x^{2}}$$ и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.
ОДЗ: $$\left | x \right |-2x^{2}\neq 0\Leftrightarrow$$ $$\left | x \right |-2\left | x \right |^{2} \neq 0\Leftrightarrow$$ $$\left | x \right |(1-2\left | x \right |)\neq 0\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq 0\\ x\neq 0,5\\ x\neq -0,5\end{matrix}\right.$$.
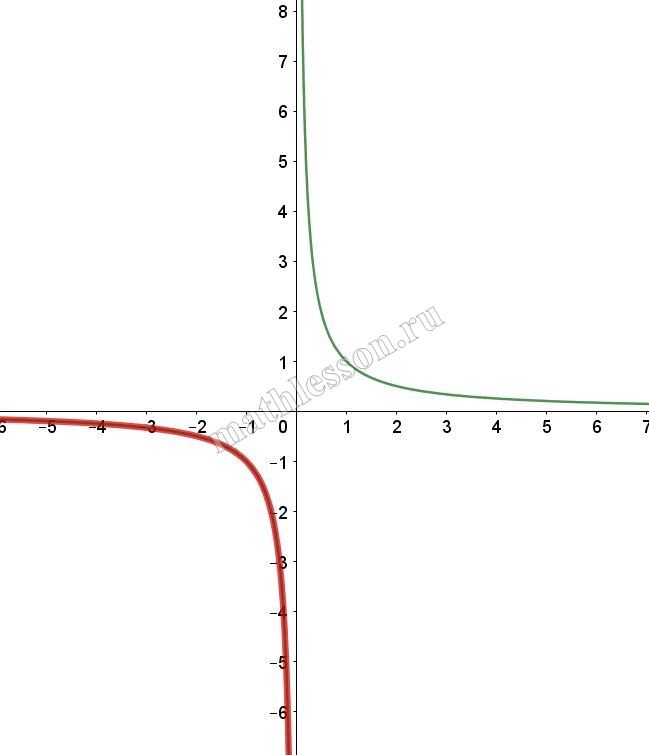
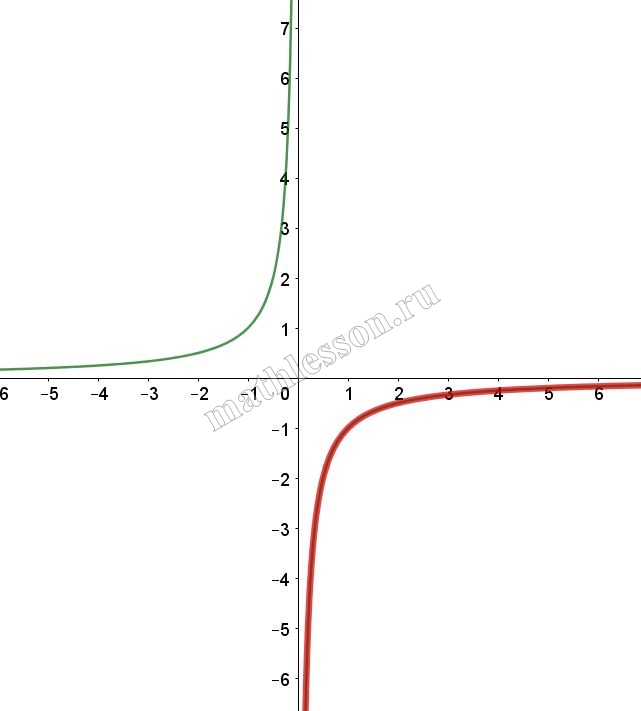
При $$x>0$$: $$y=\frac{2x-1}{x(1-2x)}=-\frac{1}{x}$$ (выдерена красным)
При $$x<0$$: $$y=\frac{-2x-1}{-x-2x^{2}}=\frac{1}{x}$$(выделена красным)
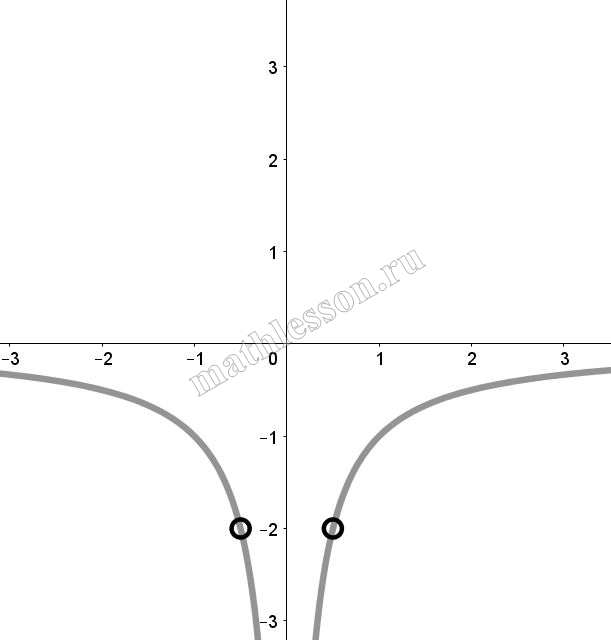
Итоговый график с учетом ОДЗ:
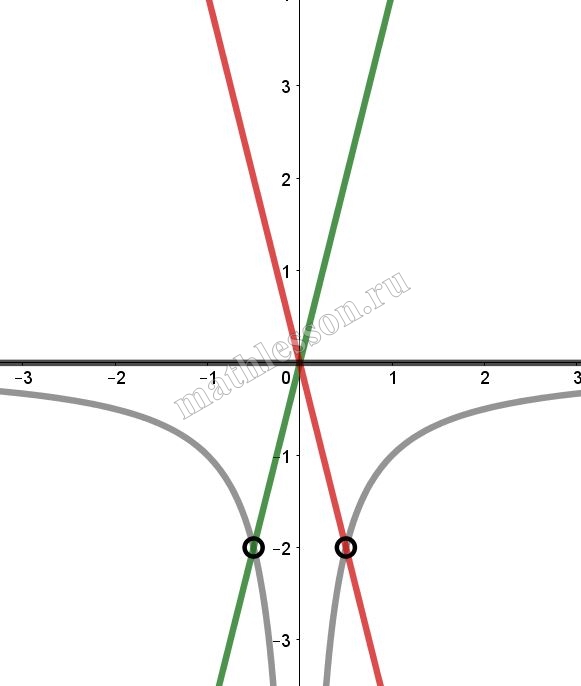
Найдем k: $$y=kx$$ проходит через (-0,5 ; -2): $$-2=-0,5*k\Rightarrow k=4$$(зеленая) и через (0,5; -2): $$-2=0,5k\Rightarrow k=-4$$(красная). При k=0 (черная) тоже не имеет пересечений
Задание 4
Диагонали параллелограмма АВСD пересекаются в точке О. В треугольнике АОВ АВ = 6 см, медиана ОК = 4 см. Найдите периметр параллелограмма АВСD.
1) Построим медиану в $$\Delta DOC$$: $$DL=LC=\frac{CD}{2}$$$$\Rightarrow$$ $$DL=AK$$, но $$DL\left | \right |AK$$$$\Rightarrow$$ $$AKLD$$ - параллелограмм $$\Rightarrow$$ $$AD=KL$$
2) $$\Delta KBO=\Delta ODL$$ ($$DC=KB$$; $$\angle BKO=\angle OLD$$; $$\angle KDO=\angle ODC$$ (накрест лежащие)) $$\Rightarrow$$ $$KO=OL=4$$
3) $$P=(6+8)*2=18$$
Задание 5
В треугольнике АВС проведена биссектриса АМ. Докажите, что если АВ+ВМ=АС+СМ, то треугольник АВС – равнобедренный
1) Пусть $$MK\perp AB$$; $$MH\perp AC$$, тогда $$\Delta AKM=\Delta AMH$$ ( по гипотенузе и острому углу) $$\Rightarrow$$ $$KM=MH$$$$\Rightarrow$$ $$BM^{2}-BL^{2}=CM^{2}-CH^{2}$$$$\Leftrightarrow$$ $$(BM-BK)(BM+BK)=(CM-CH)(CM+CH)(1)$$
2) Т.к. $$AB+BM=AC+CM(2)$$ и $$AK=AH$$, то $$BK+BM=CH+CM$$$$\Rightarrow$$ с учетом (1): $$BM-BK=CM-CH|-AH$$$$\Leftrightarrow$$ $$BM-AB=CM-AC(3)$$
3)Вычтем (2) из (3): $$2AB=2AC$$$$\Rightarrow$$ $$AB=AC$$$$\Rightarrow$$ $$\Delta ABC$$ –равнобедренный.
Задание 6
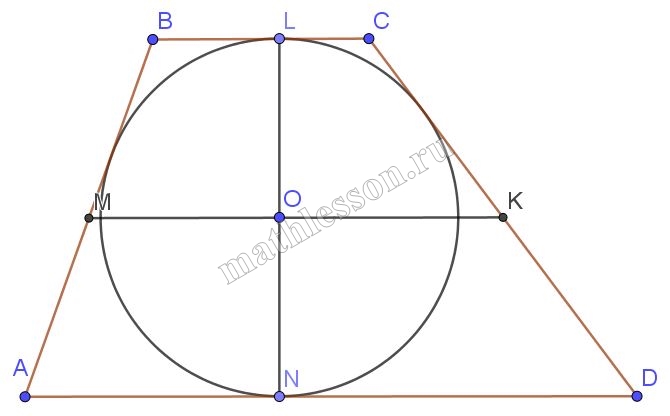
Длины боковых сторон трапеции равны 6 см и 10 см. В трапецию можно вписать окружность. Средняя линия делит трапецию на части, отношения площадей которых равно $$\frac{5}{11}$$ . Найдите длины оснований трапеции.
1) Т.к в ABCD можно вписать окружность , то $$AB+CD=BC+AD=16$$. Пусть BC=x $$\Rightarrow$$ AD=16-x
2) Пусть $$OL\perp BC$$ и $$ON\perp AD$$ (радиусы в точку касания) , и $$OL=ON=y$$; $$MK=\frac{BC+AD}{2}=8$$ - средняя линия. Тогда $$S_{MBCK}=\frac{x+8}{2}*y$$; $$S_{AMKD}=\frac{16-x+8}{2}*y=\frac{24-x}{2}*y$$
3) $$\frac{S_{MBCK}}{S_{AMKD}}=\frac{\frac{x+8}{2}*y}{\frac{24-x}{2}*y}=$$$$\frac{5}{11}\Leftrightarrow$$ $$\frac{x+8}{24-x}=\frac{5}{11}\Leftrightarrow$$ $$11x+88=120-5x\Leftrightarrow$$$$16x=32\Leftrightarrow$$ $$x=2\Rightarrow$$ $$BC=2; AD=14$$