ОГЭ математика 2019. Разбор варианта Алекса Ларина № 194.
Решаем ОГЭ 194 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №194 (alexlarin.com)
Решаем ОГЭ 194 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №194 (alexlarin.com)
Задание 1
Найдите значение выражения $$(5*10^{2})^{3}*(6*10^{-8})$$
$$(5*10^{2})^{2}*(6*10^{-8})=$$$$5^{3}*10^{2*3}*6*10^{-8}=$$$$5^{3}*6*10^{6-8}=$$$$\frac{5^{3}*6}{10^{2}}=$$$$\frac{5^{3}*6}{5^{2}*2^{2}}=$$$$\frac{5*3}{2}=7,5$$
Задание 2
В таблице даны результаты забега девочек 5-го класса на дистанцию 30 м.
| Номер дорожки | 1 | 2 | 3 | 4 |
| Время | 7,1 | 6,9 | 6,7 | 7,0 |
Зачёт выставляется, если показано время не хуже 6,8 с. Выпишите номера дорожек, по которым бежали девочки, получившие зачёт.
Время должно быть $$\leq 6,8$$, тогда зачет получила девочка с третьей дорожки .
Задание 3
Значение какого из данных выражений отрицательно, если известно, что а<0, b<0?
Варианты ответа
- ab
- (a+b)b
- (a+b)a
- -ab
Пусть a=-1, b=-2
- $$ab =(-1)(-2)=2>0$$
- $$(a+b)b=(-1-2)(-2)=6>0$$
- $$(a+b)a=(-1-2)(-1)=3>0$$
- $$-ab=-2<0$$
Задание 4
Какое из выражений равно степени $$5^{2-r}$$ ?
Варианты ответа
- $$\frac{5^{2}}{5^{r}}$$
- $$\frac{5^{2}}{5^{-r}}$$
- $$5^{2}-5^{r}$$
- $$(5^{2})^{-r}$$
$$5^{2-r}=\frac{5^{2}}{5^{r}}$$, что соответствует 1 варианту ответа .
Задание 5
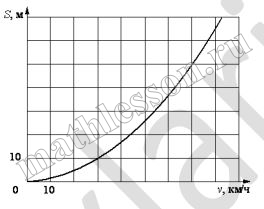
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 70 км/ч. Ответ дайте в метрах.
Тормозной путь будет составлять 50 метров
Задание 6
Решите уравнение $$\frac{x}{3}-5=\frac{x+2}{4}$$
$$\frac{x}{3}-5=\frac{x+2}{4}|*12\Leftrightarrow$$ $$4x-60=3(x+2)\Leftrightarrow$$ $$4x-3x=6+60\Leftrightarrow x=66$$
Задание 7
Орехи стоят 300 рублей за килограмм, а сухофрукты — 240 рублей за килограмм. На сколько процентов орехи дороже сухофруктов?
Пусть 250 рублей -100%, разница в цене 300-240=60 рублей , тогда
60 рублей – x%
240-100%
$$x=\frac{60*100}{240}=25$$
Задание 8
На диаграмме показаны религиозные составы населения Германии, США, Австрии и Великобритании. Определите по диаграмме, в каких странах суммарная доля протестантов и католиков превышает 75%.
Варианты ответа
Сегмент, превышающий 3/4 круга (75%) у протестантов и католиков есть только в Австрии
Задание 9
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 2, но не дойдя до отметки 5.
С 2 до 5 сектор составит 3 единицы (5-2). Всего 12 единиц на циферблате , тогда : $$P=\frac{3}{12}=0,25$$
Задание 10
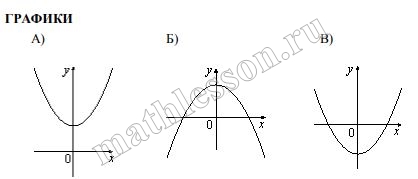
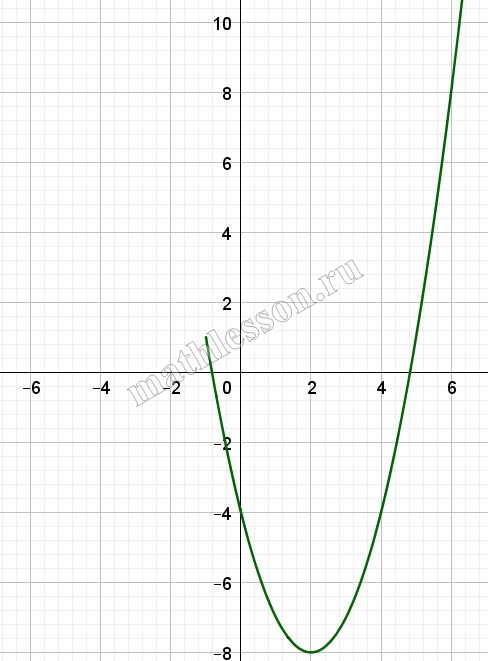
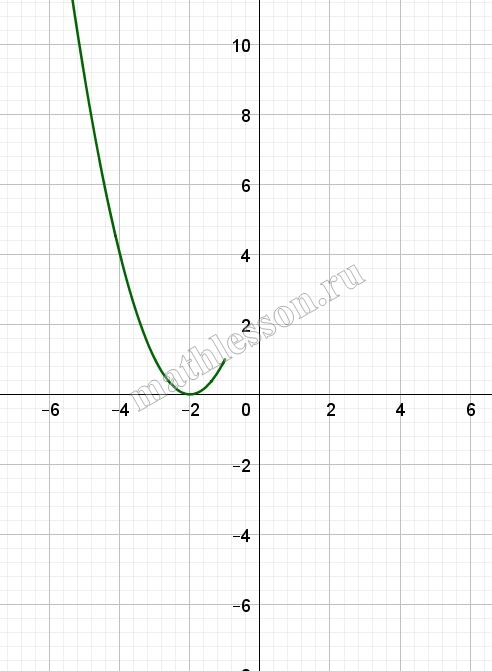
На рисунке изображены графики функций вида $$y=ax^{2}+c$$ . Установите соответствие между графиками функций и знаками коэффициентов a и c
КОЭФФИЦИЕНТЫ
- a>0, c<0
- a<0, c>0
- a>0, c>0
- a<0, c<0
a>0 –ветви параболы вверх , a<0-вниз, c>0-пересечение Oy под Ox , c<0 –под Ox
A :$$a>0, c>0\Rightarrow 3$$
B :$$a<0, c>0\Rightarrow 2$$
B :$$a>0, c<0\Rightarrow 1$$
Задание 11
Дана арифметическая прогрессия (an), для которой a4 =-12, a10 = - 78. Найдите разность прогрессии.
Чтобы найти разность арифметической прогрессии, воспользуемся формулой : $$d=\frac{a_{m}-a_{n}}{m-n}=$$$$\frac{a_{10}-a_{4}}{10-4}=$$$$\frac{-78-(-12)}{6}=-11$$
Задание 12
Найдите значение выражения $$(\frac{a+3b}{a^{2}-3ab}-\frac{1}{a}):\frac{b}{3b-a}$$, при $$a=-1,6, b=\sqrt{6}-1$$
$$(\frac{a+3b}{a^{2}-3ab}-\frac{1}{a}) :\frac{b}{3b-a}=$$$$(\frac{a+3b}{a(a-3b)}-\frac{a-3b}{a(a-3b)})* \frac{3b-a}{b}=$$$$\frac{a+3b-a+3b}{a(a-3b)}*\frac{3b-a}{b}=$$$$-\frac{6b}{ab}=-\frac{6}{a}=-\frac{6}{-1,6}=3,75$$
Задание 13
Закон Джоуля–Ленца можно записать в виде Q=I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q=378 Дж, I=3 A, R=7 Ом.
Выразим $$t=\frac{Q}{I^{2}R}$$. Найдём t: $$t=\frac{378}{3^{2}*7}=6$$
Задание 14
На каком рисунке изображено множество решений системы неравенств $$\left\{\begin{matrix}2x-3>x-7\\ 5x-2(x+1)<x-4\end{matrix}\right.$$
$$\left\{\begin{matrix}2x-3>x-7\\5x-2(x+1)-7+3\\5x-2x-x<-4+2\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>-4\\2x<-2\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>-4\\x<-1\end{matrix}\right.$$
То есть правильным ответом будет вариант под номером 3
Задание 15
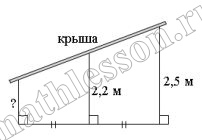
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 2,2 м, высота большей опоры 2,5 м. Найдите высоту меньшей опоры. Ответ дайте в метрах.
Пусть меньшая высота x, тогда $$\frac{x+2,5}{2}=2,2 \Leftrightarrow$$ $$x+2,5=4,4\Rightarrow x=1,9$$
Задание 16
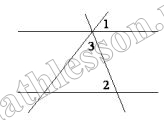
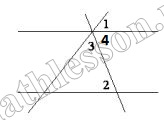
$$\angle 4=\angle 2$$-накрест лежащие, тогда: $$\angle 3=180-\angle 1-\angle 2=180-46-51=83$$
Задание 17
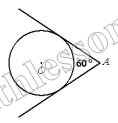
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 16.
AO-биссектриса $$\angle A\Rightarrow$$ $$\angle OAB=30$$
$$OB\perp AB$$(свойство радиуса в точку касания )$$\Rightarrow OB=OA* \sin 30=16\frac{1}{2}=8$$
Задание 18
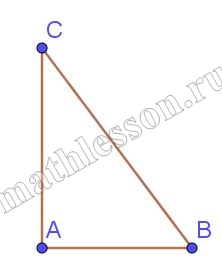
$$S=\frac{BC+AD}{2}*BH=$$$$\frac{3+7}{2}*4=20$$ Учтем, что длина клетки 5, тогда его площадь $$5*5=25$$. Тогда площадь трапеции : $$S=20*25=500$$
Задание 20
Какие из следующих утверждений верны?
- Все углы ромба равны.
- Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
- Площадь трапеции равна произведению средней линии на высоту .
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
- неверно- только противоположные
- верно
- верно
Задание 21
Найдите область определения функции $$y=\sqrt{\frac{3x^{2}-2x-5}{x-2}}$$
Область определения D(y):
$$\left\{\begin{matrix}\frac{3x^{2}-2x-5}{x-2}\geq 0\\x-2\neq 0 & &\end{matrix}\right.$$
Рассмотрим числитель дроби :$$3x^{2}-2x-5=0$$
$$D=4+60=64$$
$$x_{1}=\frac{2+8}{6}=\frac{5}{3}$$
$$x_{2}=\frac{2-8}{6}=-1$$
Получаем :
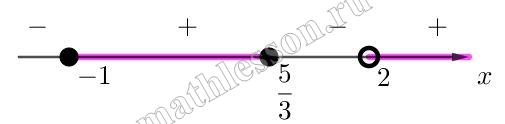
$$\left\{\begin{matrix}\frac{(x-\frac{5}{3})(x+1)}{x-2}\geq 0\\x\neq 2\end{matrix}\right.$$
Тогда: $$x\in [-1 ;\frac{5}{3}]\cup (2;+\infty )$$
Задание 22
Один рабочий должен был изготовить 36 деталей, второй – 20 деталей. Первый делал в день на 2 детали больше, чем второй, и затратил на изготовление своего заказа на 1 день меньше, чем второй. Сколько деталей в день делал каждый рабочий?
Пусть x - количество деталей в день у второго рабочего, тогда x+2 - y первого . Время заказа второго $$t_{2}=\frac{20}{x}$$ , первого $$t_{1}=\frac{36}{x+2}$$. Тогда:
$$t_{2}-t_{1}=1\Leftrightarrow$$ $$\frac{20}{x}-\frac{36}{x+2}=1\Leftrightarrow$$ $$20x+40-36x=x^{2}+2x\Leftrightarrow$$$$x^{2}+18x-40=0$$
$$\left\{\begin{matrix}x_{1}+x_{2}=-18\\x_{1}x_{2}=-40\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=-20\\x_{2}=2\end{matrix}\right.$$
Т.е. второй делал 2 детали, а первый 4
Задание 23
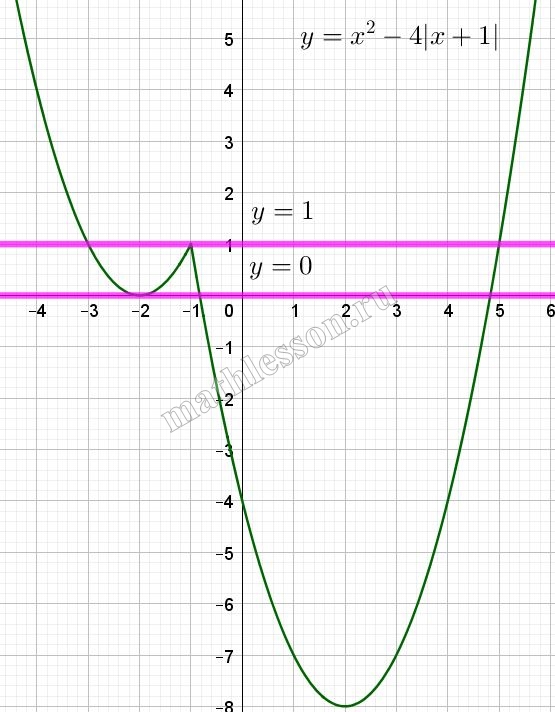
Постройте график функции $$y=x^{2}-4|x+1|$$ и определите, при каких значениях a прямая $$y=a$$ имеет с графиком ровно три общие точки.
Расмотрим подмодульное выражение:
При $$x+1\geq 0\Leftrightarrow$$ $$x\geq -1 \Rightarrow y=x^{2}-4x-4(1)$$
При $$x+1<0\Leftrightarrow$$ $$-x<-1 \Rightarrow y=x^{2}+4x+4=(x+2)^{2}(2)$$
(1): Найдём вершину: $$x_{0}=-\frac{-4}{2}=2\Rightarrow$$ $$y_{0}=2^{2}-4*2-4=-8$$
Построим график данной функции (с учетом ограничения по х):
Построим график функции (2) с учетом ограничения по х:
В итоге получаем, что три точке пересечения прямая $$y=a$$с графиком функции будет иметь при $$a=0,a=1$$
Задание 24
В равнобедренную трапецию АВСD с основаниями ВС = 18 и AD = 32 вписан круг. Найдите площадь трапеции.
1) $$BC+AD=AB+CD=18+32=50$$ ( по свойству описанного четырехугольника ), тогда AB=CD=25
2) Пусть $$BH\left | \right |CM \perp AD$$, тогда $$AH=MD=\frac{AD-BC}{2}=7$$
3) По т. Пифагора $$\Delta ABH$$: $$BH=\sqrt{25^{2}-7^{2}}=24$$
4) $$S=\frac{18+32}{2}*24=600$$
Задание 25
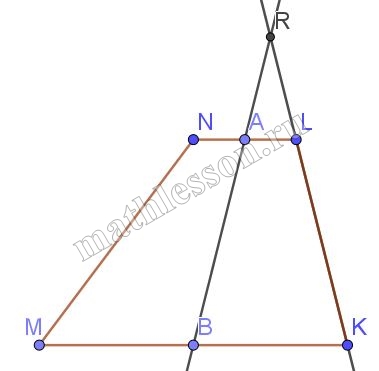
На одной из параллельных сторон трапеции взята точка А, на другой – точка В. Докажите, что отрезок АВ делится средней линией трапеции пополам.
1) Достроим $$BA\cap KL=R$$. $$\Delta ARL\sim \Delta RHH\sim \Delta BRK$$ ( т.к. $$AL\left | \right |HP\left | \right | BK$$)
2) По т. Фелеса : $$RL:LP:PK=AR: AH: HB \Rightarrow$$ $$LP :PK =1:1\Rightarrow AH: HB= 1 :1$$
Задание 26
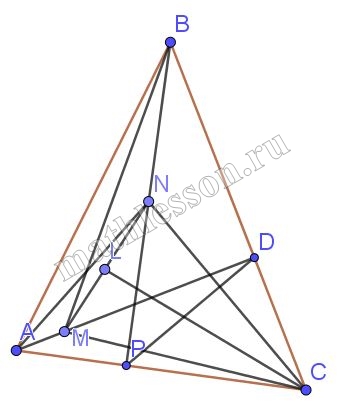
В остроугольном треугольнике АВС на высоте AD взята точка М, а на высоте ВР – точка N так, что углы ВМС и АNС – прямые. Расстояние между точками М и N равно $$4+2\sqrt{3}$$ , $$\angle MCN = 30$$. Найдите биссектрису СL треугольника CMN
1) $$\angle APB=\angle ADB=90$$ ,т.к. опирается на AB, то $$A_{1},B_{1},D_{1},P_{1}$$ лежат на одной окружности .
2) $$\angle PDA =\angle PBA$$ (вписаные , на одну дугу)
$$\angle A=90-\angle PBA(\Delta PBA)$$
$$\angle PDC=90-\angle PDA(\Delta ADC)$$
Тогда $$\angle A=\angle PDC$$, и т.к. $$\angle C$$ - общий , то $$\Delta ABC\sim \Delta PDC\Rightarrow$$ $$\frac{CB}{CP}=\frac{AC}{CD}\Leftrightarrow$$ $$AC*CP=BC*CD(1)$$
3) из $$\Delta ACN :CN^{2}=AC*CP$$
Из $$\Delta CMB: CM^{2}=BC*CD$$
С учетом (1): $$CN^{2}=CM^{2}\Rightarrow$$ $$CN=CM$$ и $$\Delta CMP$$ равнобедренный
4) Пусть CH- биссектриса , она и медиана и высота . $$NH=\frac{1}{2} NM=2+\sqrt{3}$$
$$\angle HCN=\frac{1}{2}\angle MCN=15$$
Из $$\Delta CHN \frac{HN}{HC}=tg \angle HCN\Rightarrow$$ $$HC=\frac{2+\sqrt{3}}{tg 15}$$
$$tg 15=\frac{\sin 30}{1+\cos 30}=\frac{1}{2+\sqrt{3}}$$
$$HC=(2+\sqrt{3})^{2}=7+4\sqrt{3}$$