ОГЭ математика 2023. Разбор варианта Алекса Ларина № 331.
Больше разборов на моем ютуб-канале
Задания 1-5
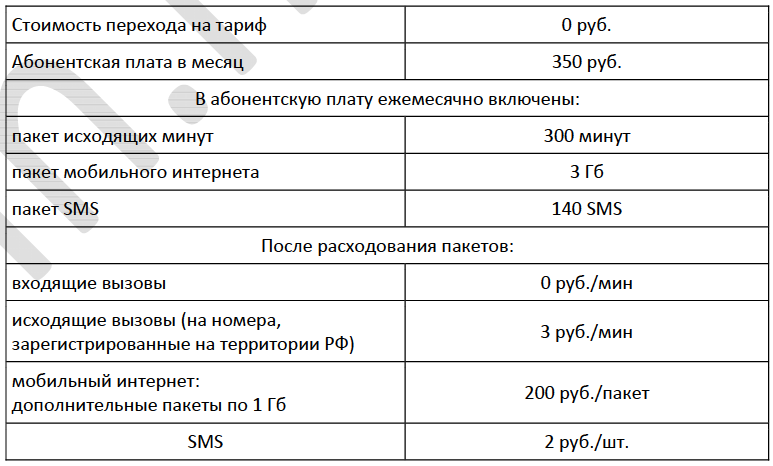
| Исходящие вызовы | 3 руб./мин |
| Мобильный интернет: дополнительные пакеты по 0,4 Гб | 90 руб. за пакет |
| SMS | 3 руб./шт. |
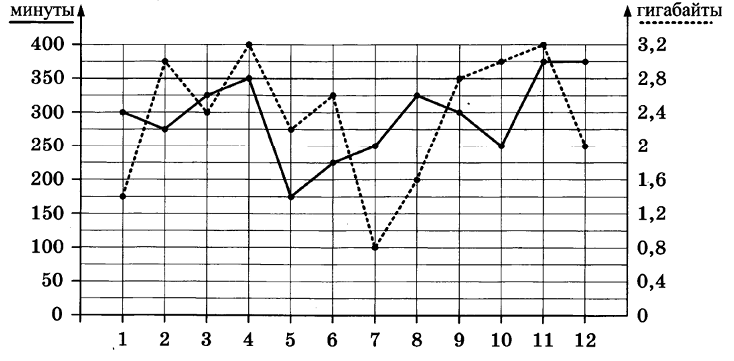
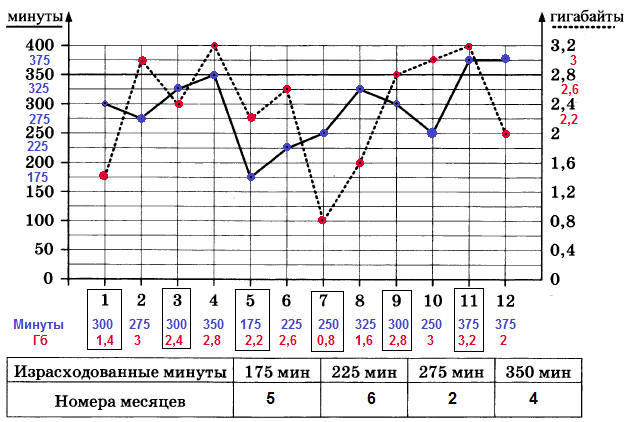
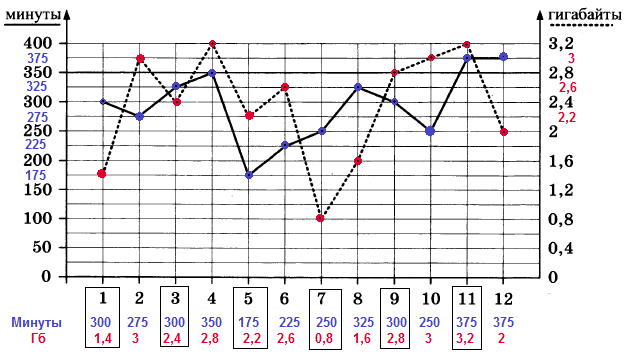
| Израсходованные минуты | 175 мин | 225 мин | 275 мин | 350 мин |
|---|---|---|---|---|
| Номера месяца |
Абонентская плата $$400$$ руб в месяц
СМС:
$$140$$ sms $$0$$ руб
Звонки:
11 месяц $$375$$ минут ($$350$$ минут входят в пакет услуг) $$375-350=25$$ минут
$$25\cdot3=75$$ руб
Интернет:
11 месяц $$3,2 ГБ$$ ($$2,8 $$ГБ входит в пакет услуг) $$3,2-2,8=0,4$$ ГБ
За пакет $$0,4$$ ГБ $$= 90$$ руб
Итого за ноябрь: $$400+75+90=565$$ руб
Звонки: Превысил лимит по звонкам $$350$$ мин в $$11$$ и $$12$$ месяцах
Интернет: Превысил лимит по интернету $$2,8$$ Гб во $$2, 4, 10, 11$$ месяцах
$$5$$ месяцев
Абонентская плата 400 руб в месяц
$$400\cdot12=4800$$ руб
СМС:
140 sms 0 руб
Превысил лимит звонков в 350 минут:
11 месяц на $$375 - 350 = 25$$ минут
12 месяц на $$375 - 350 = 25$$ минут
Доплата за звонки: $$(25+25)\cdot3=150$$ руб
Превысил Интернет 2,8 Гб:
2 месяц на $$3 - 2,8 = 0,2$$ Гб
4 месяц на $$3,2 - 2,8 = 0,4$$ Гб
10 месяц на $$3 - 2,8 = 0,2$$ Гб
11 месяц на $$3,2 - 2,8 = 0,4$$ Гб
$$\frac{0,4}{0,4}\cdot90= 90$$ руб
Доплата за интернет: $$\frac{0,2 + 0,4 + 0,2 + 0,4}{0,4}\cdot90 = 270$$ руб
ИТОГО: $$400\cdot12 + 150 + 270 = 5 220$$ руб
По новому тарифу:
Абонентская плата 350 руб в месяц
СМС:
140 sms (140 смс по тарифному плану)
Превысит лимит звонков 300 минут:
3 месяц на $$325 - 300 = 25$$ минут
4 месяц на $$350 - 300 = 50$$ минут
8 месяц на $$325 - 300 = 25$$ минут
11 месяц на $$375 - 300 = 75$$ минут
12 месяц на $$375 - 300 = 75$$ минут
Оплата за звонки: $$(25 + 50 + 25 + 75 + 75)\cdot3 = 750$$ руб
Превысит лимит интернет 3 Гб:
4 месяц на $$3,2 - 3 = 0,2$$ Гб
11 месяц на $$3,2 - 3 = 0,2$$ Гб
Оплата за интернет: $$2\cdot200 = 400$$ руб
ИТОГО по новому тарифу: $$350 * 12 + 750 + 400 = 5 350$$ руб
Новый тариф дороже.
Абонентская плата - 400 руб
Задание 6
$$-0,7\cdot(-10)^2+90=90-70=20.$$
Задание 7
Отрезок $$[8; 9]$$ можно представить в виде дробей со знаменателем $$7,$$ следующим образом:
$$[\frac{8\cdot7}{7};\frac{9\cdot7}{7}]=[\frac{56}{7};\frac{63}{7}]$$
Отсюда хорошо видно, что дробь $$\frac{61}{7}$$ принадлежит этому интервалу.
Задание 8
$$30a-5(a+3)^2=30a-5(a^2+6a+9)=30a-5a^2-30a-45=-5a^2-45$$
$$-5\cdot(\sqrt{3})^2-45=-5\cdot3-45=-15-45=-60$$
Задание 9
$$x^2+4x-45=0$$
$$D=b^2-4ac=4^2-4\cdot1\cdot(-45)=16-(-180)=16+180=196=14^2$$
$$x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-4+14}{2\cdot1}=\frac{10}{2}=5$$
$$x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-4-14}{2\cdot1}=\frac{-18}{2}=-9$$
$$x_1>x_2$$
$$x_2=-9$$ - меньший корень
Задание 10
Задание 11
Ниже представлен график некоторой функции, определённой в каждой действительной точке отрезка $$[-5; 5]$$ и не определённой вне этого отрезка. Установите соответствие между утверждениями для этой функции и их верностью. В ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
| Утверждения | Верность |
|---|---|
| А) Функция непрерывна на отрезке $$[-5; 5]$$ | 1) верно |
| Б) $$f(-1)>f(4)$$ | 2) неверно |
| В) На отрезке $$4\leq x\leq 4,2$$ функция возрастает | |
| Г) Функция имеет ровно 10 нулей функции |
А) неверно, есть разрывы на графике
Б) $$f(-1)>0;f(4)<0;f(-1)>f(4)$$ - верно
В) неверно, там она убывает
Г) верно, имеет 10 пересечений с Ox
Задание 12
Задание 13
$$8x-3(x+9)<-9\Leftrightarrow 8x-3x-27+9<0\Leftrightarrow 5x-18<0\Leftrightarrow 5x<18\Leftrightarrow$$
$$\Leftrightarrow x<3,6\Rightarrow 3$$
Задание 14
Растущее количество задач составляет арифметическую прогрессию с первым членом a1 = 11, суммой прогрессии Sn = 315 и количеством членов n = 9. Из формулы суммы арифметической прогрессии $$S_n=\frac{a_1+a_n}{2}\cdot n$$ найдем an:
$$315=\frac{11+a_n}{2}\cdot9$$
$$9(11+a_n)=630$$
$$11+a_n=70$$
$$a_n=59$$ задач
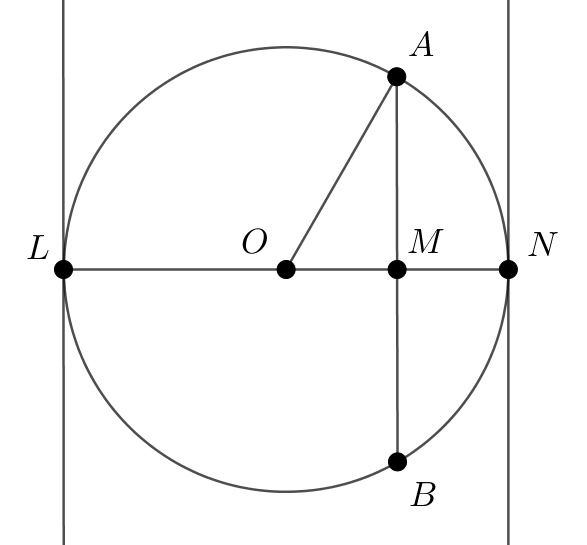
Задание 15
$$OA=50;OM\perp AB;OB=50\Rightarrow AM=MB=48\Rightarrow OM=\sqrt{50^2-48^2}=14$$
$$\Rightarrow MN=50-14=36$$
$$LM=50+14=64$$
$$LM\cdot MN=2304$$
Можно по свойству хорд: $$LM\cdot MN=AM\cdot MB=48\cdot48=2304$$
Задание 16
Радиус описанной окружности равен половине диагонали квадрата (половина синей линии), то есть, диагональ, равна:
$$d=2\cdot28\sqrt{2}=56\sqrt{2}$$
В свою очередь диагональ квадрата – это величина
$$d=\sqrt{a^2+a^2}=\sqrt{2a^2}=a\sqrt{2}$$
где a – сторона квадрата. То есть,
$$a=\frac{d}{\sqrt{2}}=\frac{56\sqrt{2}}{\sqrt{2}}=56$$
Радиус вписанной окружности равен половине стороны квадрата (половина красной линии на рисунке). Получаем:
$$r=\frac{a}{2}=\frac{56}{2}=28$$
Задание 17
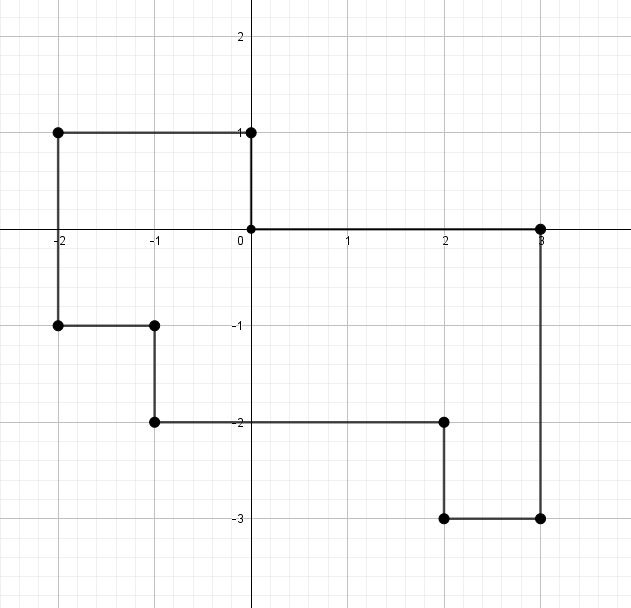
Построим данный многоугольник, где $$A_1(0;0).$$
При этом точка $$A_2(0;1),A_3(-2;1),...,A_{10}(3;0).$$
Получим 16 квадратов 1x1$$\Rightarrow S_{A_1A_2...A_{10}}=16$$
Задание 18
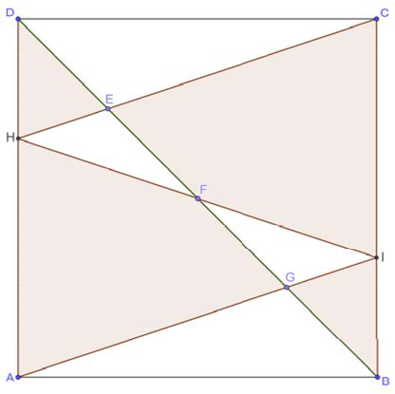
Пусть $$S_{ABCD}=S.$$ Тогда:
$$S_{ADB}=\frac{S}{2};S_{AGB}=\frac{GB}{DB}S_{ADB}=\frac{1}{4}\cdot\frac{S}{2}=\frac{S}{8};\frac{HD}{CB}=\frac{DE}{EB}=\frac{1}{3}\Rightarrow AH=\frac{2}{3}AD$$
$$S_{AHI}=\frac{2}{3}\cdot\frac{1}{2}\cdot S=\frac{1}{3}S.$$ Тогда $$S_{FGI}=\frac{1}{2}\cdot\frac{1}{4}\cdot S_{AHI}=\frac{1}{8}\cdot\frac{1}{3}S=\frac{1}{24}S$$
Итого сумма: $$(\frac{S}{8}+\frac{S}{24})\cdot2=\frac{4S}{12}=\frac{4\cdot12^2}{12}=48$$
$$AB^2+AD^2=(12\sqrt{2})^2\Rightarrow AB^2=12^2=S$$
Задание 19
1) верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
2) неверно, так как углы, заключенные между пропорциональными сторонами, не равны.
3) неверно, так как нет второго равного угла.
4) неверно, треугольник с такими сторонами является прямоугольным.
Задание 21
$$x$$ дет. в час - ученик
$$(x + 4)$$ дет. в час - мастер.
$$\frac{231}{x}-\frac{462}{x+4}=11$$
$$231(x+4)-462x=11x(x+4)$$
$$231x+924-462x=11x^2+44$$
$$-231x+924=11x^2+44x$$
$$231x+44x+11x^2-924=0$$
$$11x^2+275x-924=0$$ $$|:11$$
$$x^2+25x-84=0$$
$$D=25^2-4\cdot(-84)=625+336=961=31^2$$
$$x_1=\frac{-25+31}{2}=3$$
$$x_2=\frac{-25-31}{2}=-4$$
Второй корень не подходит, значит, ученик изготавливает $$3$$ детали в час.
Задание 22
Координата $$x$$ вершины параболы определяется по формуле $$x_n=-\frac{b}{2a}.$$ Координата $$y_в$$ вершины находится подстановкой $$x_в$$ в уравнение параболы. Вершины парабол будут находится по разные стороны от оси $$x,$$ если координаты их вершин имеют разные знаки. Вспомнив, что два сомножителя имеют разный знак тогда и только тогда, когда их произведение отрицательно, составим и решим неравенство:
$$(4p^2-8p^2-1)(-9p^2+18p^2-p)<0\Leftrightarrow(-4p^2-1)(9p^2-p)<0$$
Заметим, что первый множитель всегда меньше нуля, поэтому на него можно разделить.
$$9p(p-\frac{1}{9})>0\Leftrightarrow p(p-\frac{1}{9})>0$$
Произведение двух сомножителей будет больше нуля, если сомножители имеют одинаковый знак (см. рис.). Таким образом, получаем ответ:
$$\left[\begin{matrix} p<0\\ p>\frac{1}{9} \end{matrix}\right.$$
Задание 23
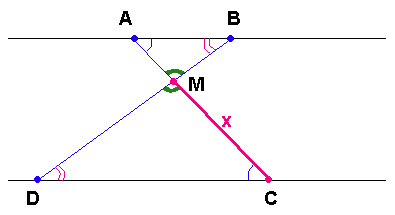
$$\Delta ABM\sim\Delta CDM$$
$$\frac{CM}{AM}=\frac{DC}{AB}$$
$$\frac{x}{56-x}=\frac{25}{10}$$
$$\frac{x}{56-x}=\frac{5}{2}$$
$$2x=5(56-x)$$
$$2x=280-5x$$
$$7x=280$$
$$x=40$$
Задание 24
Последовательно соединенные через одну вершины восьмиугольника образуют треугольники, стороны которых образованы сторонами восьмиугольника и проведенными отрезками. В правильном восьмиугольнике все стороны и углы равны. Получается, что все получившиеся треугольники равны по двум сторонам и углу между ними. Значит, все стороны у получившейся фигуры равны.
Углы у этих треугольников равны $$135; 22,5; 22,5.$$
Тогда угол фигуры можно рассчитать как: $$\frac{360 - 135 - 22,5 - 22,5}{2}=90.$$
Итак, у нас получилась фигура с углами в $$90$$ градусов и равными сторонами. То есть квадрат.
Задание 25
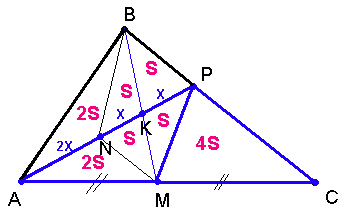
$$S_{∆KPCM}=5S$$
$$S_{∆ABC}=12S$$
$$\frac{S_{∆ABC}}{S_{∆KPCM}}=\frac{12S}{5S}=\frac{12}{5}=2,4$$