ОГЭ математика 2023. Разбор варианта Алекса Ларина № 335.
Больше разборов на моем ютуб-канале
Задания 1-5
| Урожай | Урожайность риса (г/м2) | Урожайность кукурузы (г/м2) | Урожайность пшена (г/м2) |
|---|---|---|---|
| Первый (июнь) | 600 | 1200 | - |
| Второй (сентябрь) | 800 | - | 300 |
Задание 6
$$0,0008\cdot0,008\cdot800000=8\cdot0,8\cdot8=5,12$$
Задание 7
1) $$a-b>-10\Rightarrow a>-10+b$$ - верно
2) $$b-a>32\Rightarrow -a>32-b\Rightarrow a<-32+b$$ - неверно
3) $$b-a<-4\Rightarrow -a<-4-b\Rightarrow a>b+4$$ - неверно
4) $$a-b<20\Rightarrow a<20+b$$ - неверно
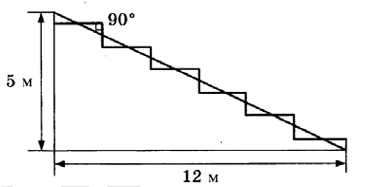
Задание 8
$$(4+a)^2-a(a-1)=16+8a+a^2-a^2+a=9a+16=9\cdot(-\frac{1}{9})+16=15$$
Задание 9
$$\left\{\begin{matrix} x^2+3x+y^2=2\\ x^2+3x-y^2=-6 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2x^2+6x=-4\\ x^2+3x-y^2=-6 \end{matrix}\right.$$
$$x^2+3x+2=0\Rightarrow\left[\begin{matrix} x_1=-2\\ x_2=-1 \end{matrix}\right.$$
При $$x=-2: 4-6-y^2=-6\Rightarrow y^2=4\Rightarrow y=\pm2$$
При $$x=-1: 1-3-y^2=-6\Rightarrow y^2=4\Rightarrow y=\pm2$$
Получим: $$(-2;-2); (-2;2); (-1;-2); (-1;2)$$
Тогда: $$10\cdot(-2)-5\cdot(-2)+2\cdot(-2)-6\cdot(-2)-8\cdot(-1)-9\cdot(-2)-2\cdot2=-4$$
Примечание от наборщика.
Ларин - чудак, такое детям в простом варианте не дают. Маразм крепчал. x2
Задание 10
$$P(A)=\frac{900-54}{900}=\frac{846}{900}=0,94$$
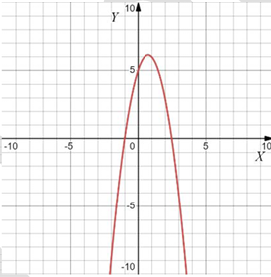
Задание 11
Если ветви вверх, то $$a>0,$$ если вниз, то $$a<0.$$
Чем "уже" парабола, тем больше $$|a|.$$
Тогда: $$1324.$$
Задание 12
$$s=330\cdot22=7260$$ м = $$7,26$$ км
Задание 13
$$\left\{\begin{matrix} \frac{6-3x}{4+(9-2x)^2}\geq0\\ 5-8x\leq23-5x \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 6-3x\geq0\\ -8x+5x\leq23-5 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x\leq2\\ x\geq-6 \end{matrix}\right.\Rightarrow x\in[-6;2]$$
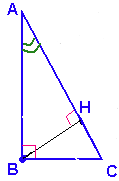
Задание 14
Задание 15
$$\Delta ABC\sim\Delta AHB$$
$$\frac{AB}{AH}=\frac{AC}{AB}$$
$$AB^2=AC\cdot AH$$
$$AB^2=36\cdot9=324$$
$$AB=18$$
Задание 16
Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны. Тем самым, угол $$OCD=25^{\circ}.$$
Задание 17
$$S=\frac{1}{2}\cdot a^2\cdot\sin\alpha=\frac{1}{2}\cdot47^2\cdot\sin150^{\circ}=\frac{47^2}{4}=552,25$$
Задание 18
Пусть $$DC=EB=HG=x; AD=EG=IH=y.$$ Тогда $$EH=EG-HG=y-x.$$ Пусть $$DC\cap IH=L.$$
Тогда $$CL=EH=y-x,$$ но $$DL=x+y-x=y.$$
Тогда $$DI=\sqrt{DL^2+LI^2}=\sqrt{y^2+x^2}$$
$$(CE=y-x=HL\Rightarrow LI=y-(y-x)=x)$$
$$DB=\sqrt{x^2+y^2}.$$ Получим $$DI=DB.$$
При этом $$\Delta ADB=\Delta DLI.$$ Тогда $$\angle ADB=\angle IDL.$$
Следовательно, $$\angle IDB=\angle ADC=90^{\circ}\Rightarrow\angle BID=\frac{90^{\circ}}{2}=45^{\circ}.$$
Задание 19
1) неверно, так как в трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон
2) неверно, так как для этого требуется условие равенства всех сторон параллелограмма.
3) верно
Задание 21
Пусть х км/ч - собственная скорость лодки, тогда х+3 км/ч - скорость лодки по течению и $$t_{1}=\frac{36}{x+3}$$ часов - время лодки по течению; х-3 км/ч - скорость лодки против течения и $$t_{2}=\frac{36}{x-3}$$ часов - время против течения. Суммарное время движения составляет 5 часов, то есть: $$t_{1}+t_{2}=5$$, получаем:
$$\frac{36}{x+3}+\frac{36}{x-3}=5|*(x-3)(x+3)\Leftrightarrow$$$$36x-108+36x+108=5x^{2}-45\Leftrightarrow$$$$5x^{2}-72x-45=0\Rightarrow$$$$D=5184+900=6084=78^{2}\Rightarrow$$$$x_{1}=\frac{72+78}{10}=15, x_{2}<0$$, то есть собственная скорость лодки составляла 15 км/ч
Задание 22
Для построения прямой достаточно двух точек.
$$x=-3: y=-3-0,5=-3,5$$
$$x=-2: y=-2-0,5=-2,5$$ (пустая, так как $$x<-2$$)
$$x=-2: y=-2\cdot(-2)-6,5=-2,5$$ (закрашенная, так как тут $$x\geq-2$$)
В итоге пустая и закрашенная дадут закрашенную.
$$x=-1: y=(-2)\cdot(-1)-6,5=-4,5.$$
$$x=-1: y=-1-3,5=-4,5.$$
$$x=0: y=0-3,5=-3,5.$$
Задание 23
Пусть BH — высота.
$$AH=8$$ и $$CH=9$$
Высота AL пересекает высоту BH в точке K:
$$BK=KH=x$$
Треугольники $$\Delta AKH, \Delta BLK$$ и $$\Delta BCH$$ подобные.
Они прямоугольные в $$\Delta AKH, \Delta BLK$$ т.к. углы $$AKH$$ и $$BKL$$ равны как вертикальные,
а $$\Delta BLK, \Delta BCH$$ имеют общий угол $$B.$$
$$\frac{KH}{AH}=\frac{CH}{BH}$$
$$\frac{x}{8}=\frac{9}{2x}$$
$$x\cdot 2x=9\cdot8$$
$$2x^2=72$$
$$x^2=36$$
$$x=6$$
$$BK=KH=6$$
$$BH=12$$
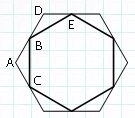
Задание 24
Рассмотрим треугольники $$ABC$$ и $$BDE.$$
Т.к. стороны правильного шестиугольника равны, то и $$CA=AB=BD=DE, \angle A=\angle D,$$ т.к. углы правильного шестиугольника тоже равны. Следовательно, данные треугольники равны (по первому признаку равенства треугольников).
Тогда $$BC=BE.$$ Углы $$\angle BCA=\angle CBA=\angle EBD=\angle BED$$ (по свойству равнобедренного треугольника). Следовательно внутренние углы $$\angle С=\angle B=\angle E.$$
Данные выкладки справедливы для любой пары треугольников, следовательно все стороны внутреннего шестиугольника равны и все внутренние углы равны. Это означает, что внутренний шестиугольник - правильный (по определению).